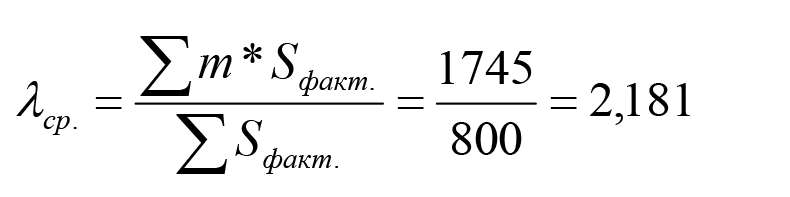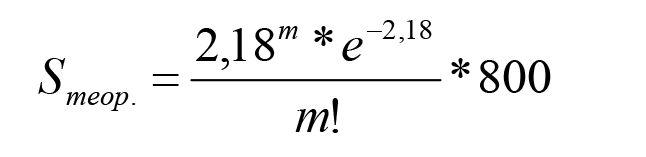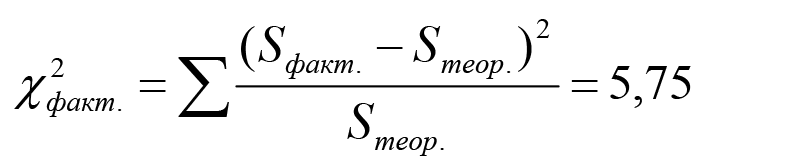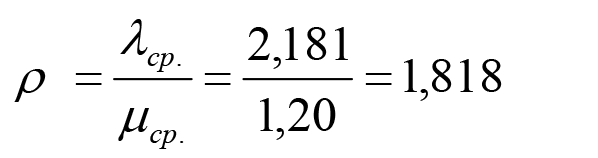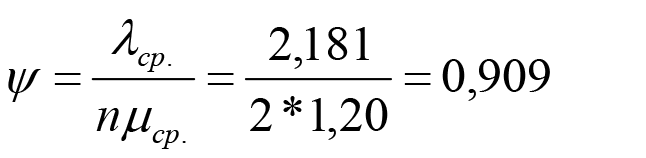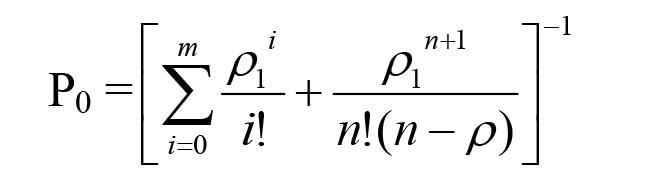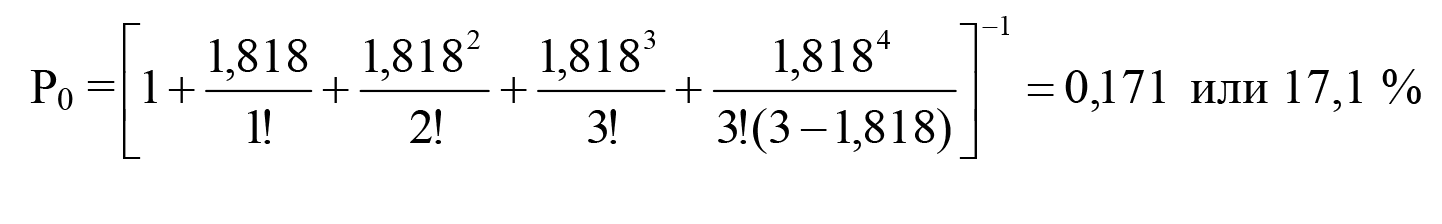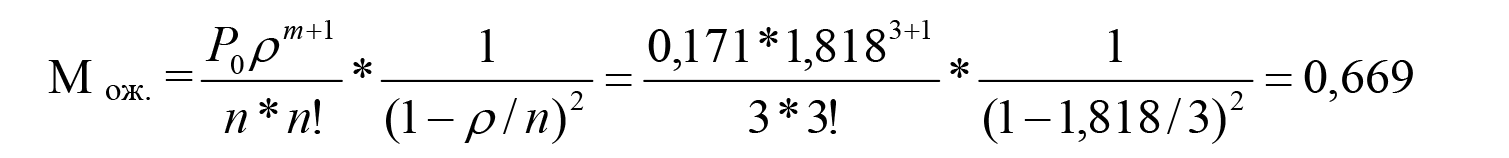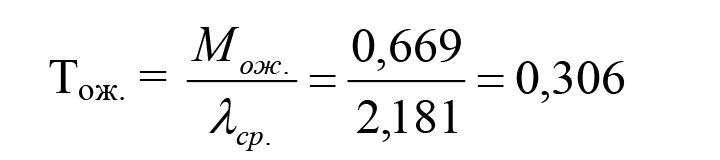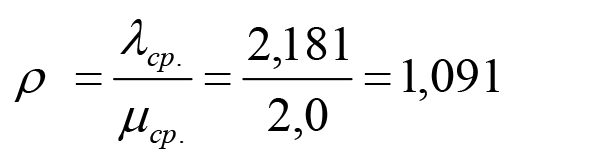Оптимизация штата сисадминов с учетом статистики инцидентов в локальной сети

Редкий сисадмин не жалуется на чрезмерную нагрузку, постоянные авралы и задержки после работы, в то время как его начальство, напротив, зачастую склонно утверждать, что для штатной должности у него мало работы, а потому его вполне можно заменить приходящим ИТ-специалистом. Очевидно, что оценки обеих сторон, сделанные без изучения объема загрузки штатного сотрудника, неизбежно грешат изрядной долей субъективизма и могут способствовать принятию ошибочного кадрового решения.

Распределение Пуассона и статистика ИТ-инцидентов

На наш взгляд, наиболее адекватным способом определения потребности компании в оптимальном штате сисадминов является использование соответствующих статистических методов, которые уже давно используется для оптимизации систем массового обслуживания (СМО). При этом основной задачей теории СМО является изучение и оптимизация режима функционирования обслуживающей системы, в том числе и с использованием методов статистики.

Вполне очевидно, что процесс поддержания в рабочем состоянии локальной ИТ-сети носит двусторонний характер. С одной стороны, то есть со стороны персонала сети, наблюдается случайный (с точки зрения времени поступления) поток требований на устранение компьютерных инцидентов – отказов в ИТ-оборудовании, которые привели к прекращению работы одного или сразу нескольких пользователей локальной сети. С другой стороны, то есть со стороны работающих в компании сисадминов, идет встречный поток работ по устранению ИТ-инцидентов, который зависит от времени их возникновения, а, следовательно, также носит случайный характер.

С точки зрения статистической науки процесс возникновения инцидентов в локальной сети можно рассматривать как случайный (стохастический) марковский процесс. Случайный процесс называется марковским в том случае, если вероятностные характеристики этого процесса в будущем, т.е. в момент времени t+1, зависят только от его состояния в настоящий момент времени t и не зависят от его предыдущих состояний.

Следует заметить, что оба встречных потока – как поток требований, сигнализирующих о возникновении инцидентов, так и поток сисадминских работ по их устранению – достаточно хорошо описывается законом распределения Пуассона. При этом пуассоновским распределением называется вероятностное распределение дискретного типа, которое моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Теперь посмотрим, как можно использовать статистические методы для оптимизации процесса устранения инцидентов в локальной сети на конкретном примере крупной компании, в которой работают два сисадмина. Допустим, что руководство этой компании, обеспокоенное слишком длительными простоями в связи с инцидентами, решило подробно изучить данную проблему с целью оптимизации штатной численности сисадминов.

На первом этапе данного исследования необходимо обеспечить подробное документирование всех инцидентов, возникающих в локальной сети. С этой целью в компании должен вестись журнал регистрации ИТ-инцидентов. При этом каждый инцидент и работы по его устранению должны фиксироваться записью, содержащей следующую информацию:

• порядковый номер инцидента;
• дату и время его возникновения;
• описание характера инцидента (какие сбои возникли в ИТ-оборудовании);
• перечень работ по устранения инцидента;
• дата и время устранения инцидента;
• причина инцидента, оценка оперативности его устранения и меры по профилактике.

По всей видимости, ведение такого рода журнала лучше поручить техническому отделу, контролирующему работу сисадминов. После того как компанией будет накоплена достаточно большая статистика по инцидентам, например, за 800 последних рабочих часов, можно приступать ко второму этапу нашего исследования.

На основе журнала регистрации ИТ-инцидентов нужно все 800 часов наблюдений сгруппировать по частоте зафиксированных инцидентов. В результате у нас получилось шесть групп наблюдений, с количеством зарегистрированных в течение каждого часа инцидентов от 0 до 5 случаев – см. таблицу 1.

Таблица 1. Фактическое и теоретическое распределение (согласно закону Пуассона) частоты инцидентов по результатам 800 часов наблюдений

Источник: расчеты автора

При этом среднее значение потока ИТ-инцидентов, а, следовательно, и потока обращений на их устранение находится по следующей формуле:

(1)

где m – количество обращений за устранением инцидентов в течение одного часа; S_факт. – фактическая (эмпирическая) частота данных обращений.

Следовательно, 800 часов наблюдений за работой локальной сети показало, что в среднем от пользователей к сисадминам поступает 2,181 обращения по поводу инцидентов в час.

Прежде чем перейти к последующим расчетам нам необходимо убедиться в том, что фактическая (эмпирическая) частота обращений по поводу инцидентов соответствует их теоретическим частотам, вычисленным согласно распределению Пуассона. При этом расчеты нужно сделать по следующей формуле:

(2)

где е – экспонента = 2,71828…

Результаты вычислений по формуле (2) можно посмотреть в таблице 1 (см. раздел «Теоретическая частота инцидентов, согласно распределению Пуассона»).

Далее проверим нулевую гипотезу о соответствии потока обращений по устранению инцидентов распределению Пуассона. С этой целью будем использовать критерий χ², фактическая величина которого рассчитывается таким образом:

(3)

где S_теор. – теоретическая частота обращений.

Результаты вычислений по формуле (3) можно посмотреть в таблице 1 в разделе «Расчеты для получения χ²_факт. по формуле (3)». Теперь сравним фактическую величину χ²_факт. с его критическим значением χ²_крит. при 5% (чаще всего используемом) уровне значимости и 4 степенях свободы. Причем, уровень значимости задается самим исследователем в зависимости от его желания получить более надежный результат (например, при 5% уровне значимости существует 5% риск сделать ошибочный вывод).

При этом число степеней свободы в нашем случае находятся следующим образом = количество групп наблюдений -2 =6-2=4; где количество групп наблюдений взято из таблицы 1 (см. раздел № группы наблюдений).

Далее находим (либо в таблице, имеющейся в приложении к любому вузовскому учебнику по статистике, либо в Excel, с помощью функции =ХИ2ОБР(0,05;4)), что при 5% уровне значимости и 4 степенях свободы критическое значение χ²_крит. = 9,49. Поскольку χ²_факт. = 5,75 ◄ χ²_крит. = 9,49, то можно сделать вывод, что поток обращений за устранением инцидента имеет пуассоновское распределение.

Благодаря ведению журнала регистрации ИТ-инцидентов нам удалось выяснить, что за 800 часов наблюдений двое сисадминов на устранение 1745 инцидентов потратили в общей сложности 1454,2 часов своего рабочего времени. Следовательно, среднее время, затрачиваемое сисадмином на устранение одного инцидента, находится следующим образом T_{ср. устр.}= 1454,2/1745=0,833*60= 50 минутам, а средняя интенсивность устранения компьютерных инцидентов μ_ср. = 1/ T_{ср. устр.}=1/0,833=1,20 инцидента в час.

Далее найдем общий параметр загрузки двух сисадминов компании работой по устранению инцидентов по следующей формуле:

(4)

где λ_ср. ‑ среднее за 1 час количество обращений к сисадминам по поводу инцидентов.

Таким образом общий параметр фактической загрузки двух сисадминов оказался лишь на 0,182 пункта ниже аналогичного уровня их полной загрузки, равного 2. Заметим, что в последнем случае предполагается, что сисадмины должны тратить все свое рабочее время лишь на устранение инцидентов.

Однако еще более наглядным является расчет другого показателя – коэффициента загрузки одного сисадмина:

(5)

где n – количество сисадминов.

Данный показатель позволяет нам сделать вывод, что 90,9% своего рабочего времени сисадимин в данной компании тратит на устранение инцидентов и лишь 9,1% – на выполнение прочих работ. Причем, в том случае, если коэффициент загрузки одного сисадмина ψ ► 1, то тогда данная СМО считается нестационарной, то есть при таком коэффициенте загрузки одного сисадмина поток обращений по поводу устранения инцидентов к нему будет постоянно нарастать.

Дело в том, что любую СМО можно представить в виде марковской непрерывной цепи, которую называют процессом гибели и размножения, поскольку графы ее состояний представляют собой цепочку, в которой каждое из промежуточных состояний связано прямой и обратной связью с каждым соседним состоянием. (См. например, «Справочник по математике для экономистов». Под ред. проф. В. И. Ермакова, – М.: Высшая школа., 1987, с. 302).

Согласно последнему определению, графы состояний двухканальной (так как в данной компании работает два сисадмина) СМО с ожиданием – для процесса работы сисадминов с обращениями по поводу инцидентов в локальной сети – будет иметь следующий вид:

Рисунок 1

На рисунке 1 символы S₀, S₁, S₂ и т.д. – обозначают различные состояния СМО, причем, их нижние индексы указывают на количество (0,1,2 и т.д.) инцидентов, с которыми в данный момент работают сисадмины. В свою очередь S_2+k – обозначает состояние СМО после достижения ею полной загрузки (когда все сисадмины заняты устранением отказов в работе локальной сети) при S₂, а нижний индекс k указывает на количество обращений пользователей, ожидающих устранения сбоя, возникшего в работе их компьютера. Направленные влево стрелки указывают на поток требований λ, которые в нестационарном СМО с ожиданием теоретически могут уйти в бесконечность; направленные вправо стрелки указывают на количество услуг μ и 2μ, предоставляемых сисадминами пользователям.

Поскольку в исследуемом нами случае коэффициент загрузки одного сисадмина равен 0,909, то, следовательно, данную СМО можно считать стационарной. Таким образом можно сделать вывод, что в данной системе массового обслуживания скорость устранения сисадминами возникающих компьютерных инцидентов в среднем превышает количество обращений пользователей за помощью. Отсюда можно сделать вывод, что в локальной сети данной компании количество инцидентов не будет расти до бесконечности, как это бывает в нестационарных СМО.

Эффект от увеличения штата сисадминов

Вполне естественно, что в зависимости от штатной численности сисадминов их коэффициент загрузки в компании будет существенно меняться – см. таблицу 2. В том случае, если бы в этой компании работал бы только один сисадмин, то тогда данная СМО была бы нестационарной. В этой ситуации сисадмину пришлось бы заниматься устранением инцидентов в течение всего рабочего времени, а также еще и оставаться сверхурочно. Причем, для устранения всех инцидентов в нестационарной СМО рабочий день сисадмина потребовалось бы увеличить в 1,817 раза!

Уже при двух сисадминах СМО в данной компании становится стационарной, правда, при этом почти все свое рабочее время им приходится заниматься лишь устранением возникающих в сети инцидентов. Если штат сисадминов в этой компании увеличить до трех человек, то в этом случае коэффициент загрузки каждого из них ψ будет равен 0,606. Иначе говоря, 60,6% своего рабочего времени они будут тратить на устранение инцидентов. Следовательно, каждый сисадмин сможет в среднем использовать 39,4% своего рабочего времени для профилактики инцидентов, а также заниматься совершенствованием локальной сети, согласно утвержденному руководством плану.

Таблица 2. Изменение коэффициента загрузки сисадминов в зависимости от их штата

Источник: расчеты автора

Вполне очевидно, что от длительных простоев, вызванных инцидентами в сети, компания может нести значительные потери. В связи с этим нужно уметь рассчитывать время, необходимое для устранения инцидента.

Поскольку нас интересует продолжительность времени, в течение которого пользователь ожидает сисадминскую помощь, то эту задачу следует решать, исходя из предположения об экспоненциальном (показательном) распределении данного интервала ожидания. Заметим, что экспоненциальное распределение представляет собой абсолютно непрерывное распределение, моделирующее время между двумя последовательными состояниями одного и того же события. В данном случае экспоненциальное распределение поможет нам смоделировать время ожидания с момента возникновения и до момента полного устранения инцидента. Правда, при этом не учитывается тот факт, что на практике очередь на устранение инцидента зависит не только от времени его возникновения, но и от серьезности ИТ-сбоя, так как предполагается, что общее количество ожидающих своего устранения инцидентов от этого не меняется.

Далее будем использовать формулы, которые применяются для СМО с ожиданием (без ограничения длины очереди), имеющих пуассоновский поток входящих требований и экспоненциально распределенное время ожидания очереди обслуживания. Например, вероятность полного простоя сисадмина (то есть когда нет ни одного обращения пользователя – на рисунке 1 это состояние обозначено символом S₀) для данного СМО можно рассчитать по следующей формуле:

(6)

где n – количество сисадминов, обслуживающих пользователей; i – нижний индекс у S₀, S₁, S₂, S_i – обозначает число обращений, поступивших в данный момент к сисадминам.

Предположим, что в компании на основе данных таблицы 2, было принято решение об увеличении штата сисадминов до трех человек. В связи с этим попробуем рассчитать вероятность ситуации, когда в локальной сети будут отсутствовать инциденты, а, следовательно, и очередь на их устранение.

Для случая, когда пользователей обслуживают три сисадмина, имеющих общий параметр загрузки в ρ=1,818 (см. формулу 4), вероятность простоя находится следующим образом:

Следовательно, при трех сисадминах и указанной выше величине общего параметра их загрузки в локальной сети компании в течение 17,1% рабочего времени будут отсутствовать не устраненные инциденты.

Следующий важный показатель – средняя длина очереди для СМО с ожиданием находится по формуле:

(7)

После чего можно найти среднее время ожидания:

(8)

Таким образом при обслуживании тремя сисадминами средняя длина очереди оказалась равна 0,669 обращениям в час, а среднее время ожидания устранения ИТ-инцидента – 0,306 часа или (0,306*60)=18,4 минутам. Для сравнения заметим, что при обслуживании двумя сисадминами средняя длина очереди в данной сети была равна 8,651 обращениям в час, а среднее время ожидания устранения инцидента – 238,0 минутам или 3 часам 58 минутам. Очевидно, увеличение штата сисадминов с двух до трех человек в данном случае можно считать вполне оправданным, в то время как прежнюю скорость обслуживания ИТ-пользователей нельзя назвать приемлемой, поскольку она наносила серьезный материальный ущерб работе компании.

Что дает сокращение времени устранения инцидента

Впрочем, простое увеличение штатной численности обслуживающего персонала далеко не всегда является оптимальным решением. Допустим, руководство компании, изучив ситуацию с инцидентами в локальной сети, могло прийти к выводу, что главной причиной их медленного устранения является квалификация сисадминов, недостаточно хорошо знающих специфику используемого программного обеспечения и ИТ- оборудования.

Если этот вывод будет признан обоснованным, то тогда вместо увеличения штатов, может быть принято решение, например, о посылке сисадминов на курсы повышения квалификации. Кроме того, в качестве дополнительной меры может быть введена система материального поощрения сисадминов за сокращение среднего времени устранения инцидента.

Допустим, что после этого время, затрачиваемое на устранение инцидентов, действительно начнет сокращаться. Теперь попробуем оценить, как интенсификация работы сисадминов повлияет на сокращение средней длины очереди и среднего времени ожидания пользователя. С этой целью будем постепенно сокращать среднее время, затрачиваемое сисадмином на устранение инцидента T_{ср. устр.}, равное 50 минутам, до 30 минут с интервалом в одну минуту. Вполне очевидно, что, например, при T_{ср. устр.} = 30 минут или =0,5 часа, средняя интенсивность устранения компьютерных инцидентов μ_ср. = 1/ T_{ср. устр.}=1/0,5 =2 инцидента в час. В свою очередь, общий параметр загрузки двух сисадминов будет равен (см. формулу 4):

Подставляя в формулы 6,7 и 8 соответствующие значения ρ₁ (для разной величины T_{ср. устр.}), вычислим значения P₀, M _ож. и T_ож. для разного среднего времени устранения инцидента в сети. При этом штатная численность сисадминов в офисе остается неизменной, то есть будет равно двум человекам. Полученные результаты поместим в таблицу 4.

Таблица 4. Улучшение качества обслуживания ИТ-пользователей тремя сисадминами при сокращении времени обслуживания 

Источник: расчеты автора

Как следует из таблицы 3, в том случае, если удастся сократить среднее время устранения инцидента с 50 до 38 минут, средняя длина очереди M _ож. уменьшиться до 0,651 инцидента в час, а среднее время ожидания пользователя T_ож. – до 17,9 минут. Таким образом оба этих важных параметра, характеризующих скорость устранения инцидентов в локальной сети, окажутся несколько лучше, чем при простом увеличении штата сисадминов с двух до трех человек.

Правда, коэффициент загрузки одного сисадмина ψ в этом случае будет равен 0,691. Следовательно, каждый из двух сисадминов сможет заниматься профилактикой и работать над совершенствованием локальной сети в среднем лишь 30,9 % своего рабочего времени. Только в случае сокращения среднего времени устранения инцидента до 33 минут эта цифра может быть увеличена до 40,0%, что несколько больше, чем при увеличении штата сисадминов до трех человек.

Основные выводы

• Наиболее адекватным способом выяснить реальную потребность компании в штатной численности сисадминов является использование статистических методов.
• Для получения статистики по инцидентам в локальной сети техническому отделу компании нужно организовать их подробное документирование с помощью журнала регистрации ИТ-инцидентов.
• Полученную статистику по инцидентам в сети необходимо проверить на соответствие фактической (эмпирической) частоты обращений по инцидентам их теоретическим частотам, вычисленным согласно распределению Пуассона.
• В том случае, если руководство компании придет к выводу о необходимости увеличения штата сисадминов, предлагаемые нами статистические методы позволяют оценить ожидаемый эффект от данной меры.
• Эффект от увеличения штата сисадминов необходимо сравнить с эффектом от сокращения среднего времени обслуживания инцидента, в том случае, если в компании существуют возможность для данного сокращения.

Очень даже познавательно. Сегодня часто приходится объяснять почему нужен штатник, или два админа, а не один. У нас было принято что как минимум два человека должны уметь выполнить определенную работу/настройку, а особо важную и срочную, то вообще все. Чтобы время реакции на событие было минимальным.

Какая-то жуткая ересь. Автор напоминает Виктора Перестукина из "Страны не выученных уроков". У того тоже для работы требовалось полтора землекопа. Вот есть в компании сетевое оборудование Cisco, SQL сервера и системы vSphere на Blade системах с дисковыми полками. И хоть как ни считай, компания будет вынуждена нанять CCNA, DBA и специалиста виртуализации. И я лично бы совсем не хотел, чтобы сервер, на котором считается моя готовая премия, вместо грамотного DBA обслуживал специалист по Cisco. А если это крупная компания и работает 24/7 то соответственно будут минимум 2 CCNA, 2 DBA и 2 виртуализатора. Потому что человеческие ресурсы, как и аппаратные компоненты, тоже нуждаются в резервировании. Дальше - еще интереснее. Есть специализация внутри направлений. Например, специалист по Citrix XenServer совсем не обязательно умеет настраивать Citrix XenDesktop. Судя по постановке вопроса, наш автор ни дня не работал с серверными и сетевыми компонентами, но зато большой любитель разглядывать "сферических коней в вакууме" С чем его и поздравляем.

Я думаю что beralex поставил перед собой задачу сказать автору свое решительное "Уу-у!", и даже обосновал это конкретными примерами. Одним словом, молодец! Только вот не потрудился понять, что здесь задача решается в общем виде. То есть эту же задачу можно решить и относительно нескольких специальностей. Просто для этого портребовалось бы несколько таких материалов. Что касается утверждения, что человеческие ресурсы нужно резервировать, то здесь как раз про это половина материала написано. См. например, Общий параметр загрузки двух сисадминов и т.д.

Ни кто не спорит что нужны специалисты по направлениям. На самом деле есть несколько проблем: - разные специализации - необходимость резервирования специалистов - попытки урезать штат до минимума Их нужно рассматривать комплексно и в каждой конкретной ситуации по своему. Это хорошо когда в компании 3 направления и 3 спеца по каждому, каждый из которых загружен как раз на 100%. Начальство считает что этого хватит. Но здесь попадаем под "среднее время устранения инцидентов" и постоянные звонки в отпуске.

Да, в жизни ситуации бывают самые разные. Сейчас стала мода отдавать ряд функций (особенно, если считают, что постоянной работы у штатного сотрудника мало) на аутсорсинг. В принципе с помощью этой математики можно посчитать, кто как загружен и надо ли переходить на аутсорсинг или выгоднее своего оставить. Вот только насколько объективно посчитают это большой вопрос.

Я читал это чудо-творение еще раньше, чем она появилась на сайте. И еще тогда сказал, что это по сути просто бумагомарательство и рекомендовал закопать подальше этот позор. Вообще мне интересно, компания, где работает сей автор, (если он вообще хоть когда-то работал техническим специалистом), применяет эти, с позволения сказать, методы??? _ Если говорить более конкретно: 1. Не указан фактор устаревания оборудования и степень наработки на отказ 2. Не указан уровень безопасности и требования к ней. 3. Не указана степень квалификации пользователей. 4. Не указано чем вообще занимаются системные администраторы. Количество звонков к специалисту по Cisco и helpdesk абсолютно разные. 5. Не учтены требования к развитию бизнеса. На практике одни и те же люди, зачастую, занимаются и развитием, и доработкой, и поддержкой уже созданного. Не учтен также момент, на каком этапе находится компания: на переходном этапе модернизации или работает в уже устоявшейся схеме. 6. Абсолютно не учтена психологическая составляющая. Люди (о чудо!) абсолютно разные. И задача, с которой холерик справится за пять минут, флегматик может выполнять пятнадцать. И это абсолютно нормально, потому что быстрое решение - не всегда правильное. Перфекционист будет данную задачу делать дольше, но зато сделает так, что за ним не надо переделывать. 7. Абсолютно не учтена квалификация сотрудников. Одно дело, когда специалисты решение "ищут по форумам" и другое дело, когда работают опытные спецы. 8. Не рассмотрена система экскалации инцидента. Вот не может человек в данный момент сам решить эту задачу. А задача очень срочная и нужная. Он просто пишет письмо на всю IT-службу с пометкой "экскалация". И дальше ВСЕ сотрудники направления и даже всей IT-службы работают над этой задачей. 9. И главное. Абсолютно нет привязки к тому, чем занимается компания. Колхоз, который картошку выращивает и трейдерская компания имеют абсолютно разные требования к IT. И если в первом случае картошка вырастет и безо всяких "программистов", то во втором случае это будут миллиардные убытки. И если в первом случае реакция руководства на один и тот же инцидент будет: "Да наплевать", то во втором случае "Вы что там все, ополоумели?!!" __________________PS.У меня большая просьба к автору: "Не надо писать таких статей. Не ровен час, прочитает этот бред какой-нибудь умник из министерства, тогда последствия разрушений будет невозможно оценить". Помните: "Мы в ответе за тех, кого приручили" (с) Антуан де Сент-Экзюпери

Господин beralex все эти ваши девять пунктов имеют право на существование. Можно, например, взять любую Вашу вводную и применить эти статистические методы. Почитайте "Справочник по математике" под редакцией проф. Ермакова - это должно вас немного успокоит. Заодно можно взять любую Вашу из 9 вводных и к ним применить эти методы. Попробуйте этим заняться. Желаю успехов!!!

Уважаемый господин Петров! Для начала ознакомьтесь пожалуйста, с правилами нашего издания http://samag.ru/main/part/5 Что-то я не вижу соблюдения данный пунктов в этой с позволения сказать, публикации. Очень надеюсь, что следующая статья этого самого автора (а может и Ваша) будет подкреплена ПРАКТИЧЕСКИМ ОПЫТОМ внедрения. Извините, но теория без без практики -- пустая трата времени. В лице меня Вы изволите видеть типичного технического специалиста и управленца, который без конкретных фактов никаким "теориям" не поверит. Вот укажете конкретный положительный пример внедрения этой самой "супертеории" в production -- вот тогда и выжмете из меня каплю доверия. А пока что, извините... От себя добавлю. Нормальному IT-директору вполне хватает калькулятора и здравого смысла, чтобы понять, что на самом деле творится у него в департаменте. Для того, чтобы понять весь "блеск и нищету" IT-службы, достаточно минут пятнадцать провести в комнате техподдержки. И никакие "формулы" тут не нужны. ____ Еще мне хочется попросить прощения у аудитории. Благодаря последнему ответу г-на Петрова стало понятно, что эта статейка писалась в расчете на то, что никто проверять не будет. Действительное, глупо тратить время на то, что нигде не востребовано. Поэтому бояться, что-то кто-то ее прочтет и кинется применять - с моей стороны было ошибочно. Я бы советовал автору прежде чем клепать подобные "материальчики" для начала ознакомиться, чем живет и дышит в реальности IT-отдел. Поработать хотя бы саппортом годика два, чтобы почувствовать на своей шкурке болезненные последствия применения новомодных "методик" IT-управления. А потом бы мы вернулись к этому разговору. А пока автор выдает опусы из серии: "Нет хлеба? Почему же они не едят пирожных!". Больше на эту "статейку от неумейки" тратить свое время не хочу и не буду. Ибо сколько сей труд не оправдывай, лучше и полезнее он не станет. __________ PS. Всех с праздником 23 февраля. Успехов удачи и побольше по-настоящему хороших статей. Всем пока!

Уважаемый господин beralex, в данном случае непонятно что вас не устраивает, допустим у вас есть люди с определенной квалификацией, есть оборудование с определенным износом. Пускай у ваших людей будет какая-то особая психология. В данном случае это не принципиально. Дальше вы собираете статистику, она, естественно, у вас будет другая. Так ведь она у всех будет другая - у всех свои проблемы. А затем вы берете формулы из данного материала и сможете (если захотите) сделать определенные выводы. Возможно в маленькой компании все можно сделать на глазок, но чем больше компания. тем вести статистику актуальнее. Хочу господина beralex и всех читателей поздравить с 23 февраля!!! Всех благ, здоровья и удачи!!!А господину beralex еще побольше здорового оптимизма!!!