|
 КИРИЛЛ ТКАЧЕНКО, инженер 1-й категории, ФГАОУ ВО «Севастопольский государственный университет», tkachenkokirillstanislavovich@gmail.com
Аналитическое моделирование
систем массового обслуживания
 Полученная программа найдет свое применение при обучении программированию не только на школьном алгоритмическом языке, но и для других языков программирования при переносе на них
Современное системное администрирование отличается повышенной сложностью. Это приводит к необходимости использования на многих этапах проектирования моделей компьютерных систем и сетей. Модели систем массового обслуживания (СМО) для этого подходят достаточно часто [1]. СМО вообще и применительно к ИТ рассмотрены во многих источниках [2-4]. Помимо указанной выше классической литературы по СМО, воедино формулы собраны вуказаниях [5].
Также стоит отметить, что аналитическая модель многоканальной СМО имеется и на языке 1С [6]. Но для школьного алгоритмического языка построение программной аналитической модели позволит впоследствии обеспечить преемственность по пути применения многих появившихся позднее сред, систем и языков разработки.
Целью настоящей работы является написание программной реализации аналитической модели многоканальной системы с буферированием.
Многоканальной СМО с буферированием является СМО типа M/M/K/N. В этой СМО имеется K каналов обработки, буфер емкости N. На вход системы поступает простейший поток заявок с интенсивностью λ, заявки обрабатываются спроизводительностью μ. Расчет основных и важных системных характеристик СМО M/M/K/N для аналитического моделирования производится по аналитическим соотношениям:
Коэффициент загрузки ρ:
 (1)
Коэффициент загрузки СМО ρs:
 (2)
Вероятность простоя СМО p0:
 (3)
Вероятность пребывания в СМО i заявок pi:
 (4)
Вероятность отказа в обслуживании заявки potk:
 (5)
Среднее число занятых каналов Kz:
 (6)
Среднее число заявок в очереди Wq:
 (7)
Среднее время ожидания заявки в очереди Tq:
 (8)
Среднее число заявок в СМО Ws:
 (9)
Среднее время пребывания заявки в СМО Ts:
 (10)
По этим формулам (1)-(10) уже можно осуществлять написание программы для аналитического моделирования.
Основной алгоритм SAMAG выполняет расчет СМО M/M/4/7 с λ = 30 и μ = 17:
алг SAMAG
нач
СМО(4, 7, 30, 17);
кон
Алгоритм СМО (цел K, цел N, вещ lam, вещ mu) производит расчет СМО типа M/M/K/N, в которой λ = lam и μ = mu. Для обеспечения расчета определяются переменные, которые соответствуют входящим в формулы (1)-(10), а именно:
- rho – ρ – коэффициент загрузки,
- rhos – ρs – коэффициент загрузки СМО,
- p0 – p0 – вероятность простоя СМО,
- potk – potk – вероятность отказа в обслуживании заявки,
- Kz – Kz – среднее число занятых каналов,
- Wq – Wq – среднее число заявок в очереди,
- Tq – Tq – среднее время ожидания заявки в очереди,
- Ws – Ws – среднее число заявок в СМО,
- Ts – Ts – среднее время пребывания заявки в СМО.
Также в качестве счетчиков циклов служат переменные i и j, а для накопления произведений в числителях и знаменателях сумм – Числ, Знам и KФакт:
алг СМО(цел K, цел N, вещ lam, вещ mu)
нач
вещ rho, rhos;
вещ p0, potk;
вещ Kz;
вещ Wq, Tq;
вещ Ws, Ts;
вещ psost;
цел i, j;
вещ Числ, Знам;
вещ KФакт;
Расчет коэффициента загрузки ρ производится по соотношению (1). На этом этапе работы программы и далее рассчитанная величина с указанием ее наименования выводится для пользователя с четырьмя знаками дробной части:
rho := lam / mu;
вывод "rho = ", rho:6:4, нс;
Аналогичным образом по соотношению (2) определяется значение коэффициента загрузки СМО ρs:
rhos := rho / K;
вывод "rho_s = ", rhos:6:4, нс;
Для расчета вероятности простоя СМО p0 (3) происходит в цикле с параметром накопление величины суммы. Для процесса накопления производится расчет отдельно числителя и знаменателя. После окончания процесса накопления полученные значения числителя и знаменателя также продолжают использоваться в расчете p0:
p0 := 1;
Числ := 1;
Знам := 1;
нц для j от 1 до K - 1
Числ := Числ * rho;
Знам := Знам * j;
p0 := p0 + Числ / Знам;
кц
Числ := Числ * rho * (1 - rhos ** (N + 1));
KФакт := Знам * K;
p0 := p0 + Числ / (KФакт * (1 - rhos));
p0 := 1 / p0;
вывод "p0 = ", p0:6:4, нс;
Вероятность отказа в обслуживании заявки potk непосредственно получается по формуле (5):
potk := (rho ** (K + N) * p0) / (KФакт * K ** N);
вывод "potk = ", potk:6:4, нс;
Также явно рассчитывается и среднее число занятых каналов Kz по формуле (6):
Kz := rho * (1 - potk);
вывод "Kz = ", Kz:6:4, нс;
Для удобства среднее число заявок в очереди Wq по формуле (7) определяется по разделенной на части формуле:
Wq := (rho ** (K + 1) * p0) / (KФакт * K);
Wq := Wq * (1 - (rhos ** N) * (N + 1 - N * rhos)) / (1 - rhos) ** 2;
вывод "Wq = ", Wq:6:4, нс;
Расчет среднего времени ожидания заявки в очереди Tq по формуле (8) достаточно прост:
Tq := Wq / lam;
вывод "Tq = ", Tq:6:4, нс;
Как и среднего числа заявок в СМО Ws по формуле (9):
Ws := Wq + Kz;
вывод "Ws = ", Ws:6:4, нс;
И среднего времени пребывания заявки в СМО Ts по формуле (10):
Ts := Tq + (1 - potk) / mu;
вывод "Ts = ", Ts:6:4, нс;
В свою очередь, в конец алгоритма вынесены расчеты вероятности пребывания в СМО i заявок pi по формуле (4). Реализация определения значений по (4) программно в некоторой степени аналогична (3). В частности, отдельно рассчитываются числители и знаменатели слагаемых, когда число заявок не превышает число каналов (1 ≤ i ≤ K):
Числ := p0;
Знам := 1;
нц для i от 1 до K
Числ := Числ * rho;
Знам := Знам * i;
psost := Числ / Знам;
вывод "p", i, " = ", psost:6:4, нс;
кц
Поскольку в случае, когда число заявок больше числа каналов (K< i ≤ K+N), расчет несколько отличается, то он реализовывается в отдельном цикле с параметром, в котором также применяются ранее сформированные величины числителей и знаменателей:
нц для i от K + 1 до K + N - 1
Числ := Числ * rho;
Знам := Знам * K;
psost := Числ / Знам;
вывод "p", i, " = ", psost:6:4, нс;
кц
кон
Полный исходный текст программы на школьном алгоритмическом языке вы можете скачать на сайте журнала http://samag.ru.
Результаты работы программы:
rho = 1.7647
rho_s = 0.4412
p0 = 0.1678
potk = 0.0002
Kz = 1.7643
Wq = 0.0943
Tq = 0.0031
Ws = 1.8586
Ts = 0.0620
p1 = 0.2961
p2 = 0.2613
p3 = 0.1537
p4 = 0.0678
p5 = 0.0299
p6 = 0.0132
p7 = 0.0058
p8 = 0.0026
p9 = 0.0011
p10 = 0.0005
Фрагмент запущенной среды разработки – на рис. 1.
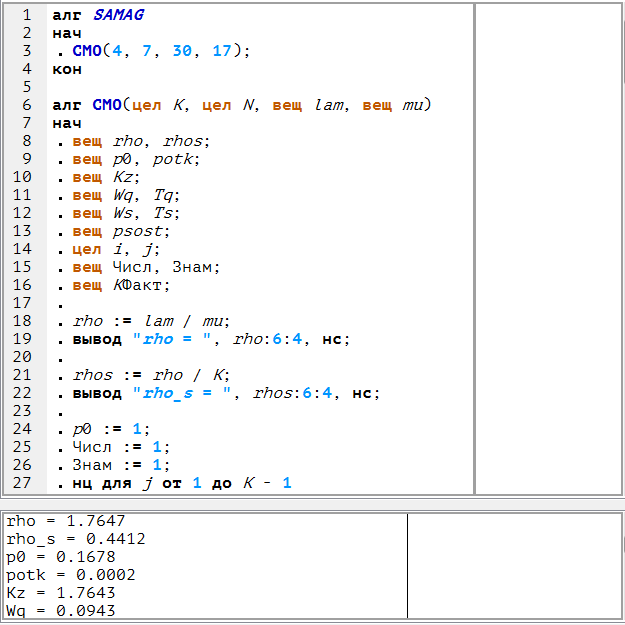
Рисунок 1. Фрагмент запущенной среды разработки
Полученная программа найдет свое применение при обучении программированию не только на школьном алгоритмическом языке, но и для других языков программирования при переносе на них.
- Клейнрок Л. Вычислительные системы с очередями. – М.: Мир, 1979. – 600 с.
- Клейнрок Л. Теория массового обслуживания. – М.: Машиностроение, 1979. – 432 с.
- Вентцель Е.С. Теория вероятностей / Е.С. Вентцель, Л.А. Овчаров. – М.: Наука, 1973. – 368 с.
- Новиков О.А. Прикладные вопросы теории массового обслуживания / О.А. Новиков, Б.В. Гнеденко, С.И. Петухов. – М.: Советское радио, 1969. – 398 с.
- Балакирева И.А. Методические указания для выполнения типовой выпускной квалификационной работы бакалавра по тематике анализа эффективности компьютерных систем обработки данных / И.А. Балакирева, А.В. Скатков. – Севастополь: СевГУ, 2015. – 32 с.
- Ткаченко К. Аналитическое моделирование в 1С многоканальной системы массового обслуживания. // «Системный администратор», № 11, 2018 г. – С.36-37. URL: http://samag.ru/archive/article/3758.
Ключевые слова: системы массового обслуживания, аналитическое моделирование, школьный алгоритмический язык.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
Аналитическое моделирование систем массового обслуживания
