|
 КИРИЛЛ ТКАЧЕНКО, инженер 1-й категории, ФГАОУ ВО «Севастопольский государственный университет», tkachenkokirillstanislavovich@gmail.com
Простейший рекурсивный алгоритм
с возвратом и эвристикой решения задачи о ходе коня
 Рассматривается реализация рекурсивного алгоритма с возвратом. Решается задача о ходе коня при использовании эвристики по Варнсдорфу для сокращения перебора. Программа реализовывается на школьном алгоритмическом языке, приводятся полный исходный текст и результаты работы
Изучение и совершенствование программирования, возможно, целесообразно производить на решении классических задач, для которых программная реализация имеет умеренную сложность.
Одной из таких задач является классическая задача о ходе коня [1], которая сводится к построению маршрута коня на шахматной доске, покрывающего все клетки доски. Для нее известны многочисленные программные реализации наПаскале [1] и подобным ему языкам, хрестоматийные программные реализации [2] и на языке 1С [3]. Для начального обучения программированию подходит школьный алгоритмический язык.
Целью публикации является разработка программной реализации на школьном алгоритмическом языке рекурсивного алгоритма с возвратом для решения классической задачи о ходе коня на шахматной доске с использованием эвристики поВарнсдорфу для сокращения перебора.
В целочисленных переменных N находится размер стороны шахматной доски, NN – количество клеток шахматной доски, Ndydx – наибольшее возможное число ходов из одной клетки для коня:
цел N = 8
цел NN
цел Ndydx = 8
В одномерных целочисленных массивах dy и dx хранятся приращения координаты для возможного хода коня из конкретной клетки шахматной доски:
цел таб dy[1:Ndydx]
цел таб dx[1:Ndydx]
Сама шахматная доска располагается в двумерном целочисленном массиве доска, на каждой клетке массива находится номер хода коня при посещении клетки:
цел таб доска[1:N, 1:N]
Целочисленные переменные кодСимволаA1 и лучшийВесНач хранят соответственно код символа «a» минус 1 и лучший начальный вес для эвристики:
цел кодСимволаA1
цел лучшийВесНач
Головной алгоритм выполняет инициализацию, после устанавливает на поле a1 коня:
алг SAMAG
нач
Инициализация
доска[1, 1] := 1;
Если из поля a1 возможно решение, то заполненная перемещениями коня шахматная доска печатается, иначе решений нет:
если Решить(2, 1, 1)
то
ПечатьДоски;
иначе
вывод "Нет решений.", нс;
все
кон
Алгоритм Инициализация производит установку начальных значений переменных. Целочисленные переменные у и x – счетчики циклов:
алг Инициализация
нач
цел y, x;
В целочисленную переменную NN помещается количество клеток шахматной доски, в кодСимволаA1 – код символа «a» минус 1:
NN := N * N;
кодСимволаA1 := код("a") - 1;
Заполняются приращения координаты dy:
dy[1] := 2;
dy[2] := 1;
dy[3] := -1;
dy[4] := -2;
dy[5] := -2;
dy[6] := -1;
dy[7] := 1;
dy[8] := 2;
Заполняются приращения координаты dx:
dx[1] := 1;
dx[2] := 2;
dx[3] := 2;
dx[4] := 1;
dx[5] := -1;
dx[6] := -2;
dx[7] := -2;
dx[8] := -1;
Лучший начальный вес полагается равным (Ndydx+1)2:
лучшийВесНач := (Ndydx + 1) * (Ndydx + 1);
Конь вначале не посетил ни одной клетки шахматной доски:
нц для y от 1 до N
нц для x от 1 до N
доска[y, x] := 0;
кц
кц
кон
Алгоритм ПечатьДоски выводит на устройство вывода шахматную доску. Целочисленные переменные y, x – счетчики циклов:
алг ПечатьДоски
нач
цел y, x;
Сообщаются по каждой горизонтали соответствующие клетки шахматной доски:
нц для y от N до 1 шаг -1
вывод y, " ";
нц для x от 1 до N
вывод доска[y, x]:4;
кц
вывод нс;
кц
Затем отображаются номера вертикалей:
вывод " ";
нц для x от 1 до N
вывод " ", символ(кодСимволаA1 + x);
кц
вывод нс;
кон
Алгоритм МожноХодить возвращает «да», если клетка с целочисленными координатами y и x принадлежит шахматной доске и на нее конь не ходил, и «нет», в противном случае:
алг лог МожноХодить(цел y, цел x)
нач
знач := (1 <= y) и (y <= N) и (1 <= x) и (x <= N) и (доска[y, x] = 0);
кон
Алгоритм ЛучшийХод с учетом эвристики по Варнсдорфу для расположения коня в клетке с координатами y и x возвращает номер направления перемещения, пригодного для использования в качестве индекса массивов dy и dx. Вцелочисленных переменных лучшееНапр и лучшийВес находятся найденные лучшее направление перемещения и вес для него, напр, напр2, вес – номер направления перемещения, номер следующего за ним направления, вес по следующему направлению рассчитанный, ny, nx – новые координаты местоположения коня с учетом приращений координат:
алг цел ЛучшийХод(цел y, цел x)
нач
цел лучшееНапр, лучшийВес;
цел напр, напр2, вес;
цел ny, nx;
Вначале лучшее направление перемещения неопределенно и лучшим весом направления перемещения считается наибольший возможный с запасом:
лучшееНапр := -1;
лучшийВес := лучшийВесНач;
По всем номерам возможных направлений перемещения коня формируется новое положение коня:
нц для напр от 1 до Ndydx
ny := y + dy[напр];
nx := x + dx[напр];
Если в эту клетку шахматной доски можно ходить, то производится оценка веса этой клетки:
если МожноХодить(ny, nx)
то
вес := 0;
Для этого подсчитывается количество клеток доски, в которые из рассматриваемой клетки возможен переход конем, то есть вес клетки доски:
нц для напр2 от 1 до Ndydx
если МожноХодить(ny + dy[напр2], nx + dx[напр2])
то
вес := вес + 1;
все
кц
Если вес меньше лучшего, то запоминаются направление и вес:
если вес < лучшийВес
то
лучшееНапр := напр;
лучшийВес := вес;
все
все
кц
Возвращается значение номера лучшего по эвристике направления:
знач := лучшееНапр;
кон
Алгоритм Решить ищет решение рекурсивно начиная с хода коня номерХода, когда конь находится на клетке шахматной доски с координатами y и x. В целочисленных переменных содержатся: напр – номер направления в любом измассивов с приращениями, ny, nx – координаты клетки, куда конь пойдет:
алг лог Решить(цел номерХода, цел y, цел x)
нач
цел напр;
цел ny, nx;
Если номер хода коня превышает число клеток, то успешное завершение:
если номерХода > NN
то
знач := да;
выход;
все
Иначе определяем лучшее направление перемещения и координаты для хода коня:
напр := ЛучшийХод(y, x);
ny := y + dy[напр];
nx := x + dx[напр];
Если конь этот ход может совершить, то он его совершает:
если МожноХодить(ny, nx)
то
доска[ny, nx] := номерХода;
Если допускается решение из совершенного хода, то ус-пешное завершение, иначе происходит отмена хода коня:
если Решить(номерХода + 1, ny, nx)
то
знач := да;
выход;
иначе
доска[ny, nx] := 0;
все
все
В любом другом случае решений нет:
знач := нет;
кон
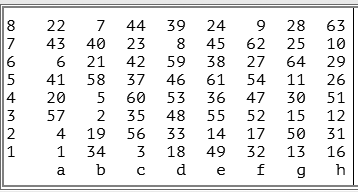
Рисунок 1. Результаты работы программы
Полный исходный текст программы находится на сайте журнала http://samag.ru. Статья позволят изучать и совершенствовать программирование на примере классической задачи информатики с умеренной сложностью.
- Вирт Н. Алгоритмы + структуры данных = программы / Н. Вирт. – М.: Мир, 1985. 406 с.
- Knight's tour // Rosetta Code. URL: http://rosettacode.org/wiki/Knight's_tour (дата обращения: 04.10.2018).
- Ткаченко К. Простейший рекурсивный алгоритм с возвратом и эвристикой в 1С на примере задачи о ходе коня. // «Системный администратор», № 1-2, 2018 г. – С. 65-67. URL: http://samag.ru/archive/article/3584 (дата обращения:04.10.2018).
Ключевые слова: задача о ходе коня, рекурсивный алгоритм с возвратом, рекурсивный алгоритм с эвристикой, школьный алгоритмический язык.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
Простейший рекурсивный алгоритм с возвратом и эвристикой решения задачи о ходе коня
