 |
|
|
|
Простейший рекурсивный алгоритм с возвратом и эвристикой в 1С на примере задачи о ходе коня
Простейший рекурсивный алгоритм
|
КИРИЛЛ ТКАЧЕНКО, инженер 1-й кат., ФГАОУ ВО «Севастопольский государственный университет», | Проясним практические ситуации для операторов и функций 1С, как для методов поиска решения, так и для задач обработки информации |
Одной из них является задача о ходе коня, состоящая в поиске пути коня по всем клеткам шахматной доски. Для нее существует большое количество решений, в том числе и учебных [1]. Но реализация переборного алгоритма напрямую, без оптимизаций и улучшений, приведет к резкому росту числа просматриваемых вариантов и, следовательно, потреблению вычислительных ресурсов, в том числе времени поиска решения. Уменьшить число вариантов можно, применив правило Варнсдорфа, согласно которому необходимо выбирать те позиции для следующего хода коня, откуда можно сделать наименьшее количество возможных переходов. Это правило часто употребляется, поскольку допускает достаточно простую программную реализацию и при этом обеспечивает высокое быстродействие и производительность [2].
Целью настоящей работы является описание разработанной программы на языке 1С для решения задачи о ходе коня на основе рекурсивного алгоритма с возвратом с ограничением на возможные ходы по правилу Варнсдорфа.
Для достижения поставленной цели создается новая пустая конфигурация 1С. В Конструкторе открывается на редактирование модуль управляемого приложения. В этом модуле в дальнейшем вводятся программные коды.
Начало программы состоит в определении переменных для всех ее подпрограмм:
Перем N, NN;
Перем dy, dx;
Перем Доска;
Перем КодСимволаA;
Перем ЛучшийВесНач;
В N находится размер доски, а именно 8 клеток, в NN – общее количество клеток, N * N = 64. Массивы dy и dx хранят приращения для перехода коня с одной клетки доски на другую: dx по оси абсцисс, dy по оси ординат. Будет производиться поиск только одного, первого, найденного решения, поэтому не учитывается симметрия. В двумерном массиве Доска на пересечении y строки и x столбца размещается номер хода от 1 до NN, на котором конь посетит соответствующую клетку. КодСимволаA содержит код символа «a» для вывода строкового представления доски, а ЛучшийВесНач – начальное значение лучшего веса, которое заведомо превосходит по величине любой возможный вес для эвристики.
Процедура Инициализация() содержит код для начальной инициализации поиска решения. Вначале находится определение переменных и наполнение их значениями:
Процедура Инициализация()
Перем y, x;
N = 8;
NN = N * N;
КодСимволаA = КодСимвола("a");
Переменные y и x выполняют роль счетчиков циклов с параметрами, N и NN получают значения 8 и 64, КодСимволаA – соответствующий код буквы «a». После значениями наполняются массивы приращений координат, вначале dy:
dy = Новый Массив();
dy.Добавить(2);
dy.Добавить(1);
dy.Добавить(-1);
dy.Добавить(-2);
dy.Добавить(-2);
dy.Добавить(-1);
dy.Добавить(1);
dy.Добавить(2);
Затем dx:
dx = Новый Массив();
dx.Добавить(1);
dx.Добавить(2);
dx.Добавить(2);
dx.Добавить(1);
dx.Добавить(-1);
dx.Добавить(-2);
dx.Добавить(-2);
dx.Добавить(-1);
От числа элементов в любом из массивов с приращениями зависит величина, находящаяся в ЛучшийВесНач:
ЛучшийВесНач = (dy.Количество() + 1) * (dy.Количество() + 1);
Наконец, Доска становится пустой:
Доска = Новый Массив(N, N);
Для y = 0 По N - 1 Цикл
Для x = 0 По N - 1 Цикл
Доска[y][x] = 0;
КонецЦикла;
КонецЦикла;
КонецПроцедуры
Поскольку решение требуется отобразить, то создается процедура для этих целей ПечатьДоски(), начинающаяся с объявления переменных:
Процедура ПечатьДоски()
Перем Рез;
Перем y, x;
Рез = "";
В Рез содержится строка-результат, начальное значение которой – пустая строка, y и x – счетчики циклов. Циклический процесс формирует единую строку из содержимого двумерного массива Доска:
y = N - 1;
Пока y >= 0 Цикл
Рез = Рез + Строка(y + 1) + " ";
Для x = 0 По N - 1 Цикл
Рез = Рез + Прав(" " + Строка(Доска[y][x]), 4);
КонецЦикла;
Рез = Рез + ""
"";
y = y - 1;
КонецЦикла;
Для строки массива фрагмент строки-результата начинается с номера горизонтали, затем следуют номера ходов коня, на котором были посещены соответствующие клетки игрового поля, в конце помещается терминатор. После этого добавляются номера вертикалей и строка сообщается пользователю:
Рез = Рез + " ";
Для x = 0 По N - 1 Цикл
Рез = Рез + " " + Символ(КодСимвола("a") + x);
КонецЦикла;
Сообщить(Рез);
КонецПроцедуры
Функция МожноХодить(y, x) для координат y и x определяет, можно ли ходить:
Функция МожноХодить(y, x)
Возврат (0 <= y) И (y < N) И (0 <= x) И (x < N) И (Доска[y][x] = 0);
КонецФункции
Для существования хода коня необходимо, чтобы координаты принадлежали клетке поля и в нее конь еще не совершал хода. Эта функция не учитывает разницу с исходной игровой клеткой, поскольку соответствующая задача ложится на вызывающую подпрограмму.
Эвристический выбор варианта по Варнсдорфу сосредоточен в функции ЛучшийХод(y, x) для коня с координатами y и x:
Функция ЛучшийХод(y, x)
Перем ЛучшееНапр, ЛучшийВес;
Перем Напр, Напр2, Вес;
Перем ny, nx;
ЛучшееНапр = -1;
ЛучшийВес = ЛучшийВесНач;
Эта функция начинается с определения переменных, в которых хранится номер лучшего найденного направления ЛучшееНапр в массивах с приращениями, наименьший вес для него ЛучшийВес, счетчик перебора направления на текущем шаге Напр и непосредственно следующим за ним Напр2, рассчитанный вес направления Вес, а также возможные координаты следующего хода, сдвинутые на приращения ny (ось ординат) и nx (ось абсцисс). ЛучшееНапр и ЛучшийВес получают невозможные значения: -1 и ЛучшийВесНач соответственно. После этого для всех возможных направлений перехода выполняется просмотр в цикле со счетчиком:
Для Напр = 0 По dy.Количество() - 1 Цикл
ny = y + dy[Напр];
nx = x + dx[Напр];
Вычисляются приращенные величины координат для хода коня. Выполняется проверка возможности перехода коня:
Если МожноХодить(ny, nx) Тогда
Вес = 0;
Для Напр2 = 0 По dy. Количество() - 1 Цикл
Если МожноХодить(ny + dy[Напр2], nx + dx[Напр2]) Тогда
Вес = Вес + 1;
КонецЕсли;
КонецЦикла;
Если переход возможен, то уже для следующей ячейки выполняется просмотр возможных ходов. При этом подсчитывается их количество. При условии, что этот вес меньше найденного:
Если Вес < ЛучшийВес Тогда
ЛучшееНапр = Напр;
ЛучшийВес = Вес;
КонецЕсли;
КонецЕсли;
Запоминаются номер рассматриваемого направления первого уровня вложенности и вес для него. Это направление возвращается из функции:
КонецЦикла;
Возврат ЛучшееНапр;
КонецФункции
Поиск решения рекурсивно исполняется функцией Решить(Шаг, y, x) для номера шага Шаг и текущих координат коня y и x:
Функция Решить(Шаг, y, x)
Перем Напр;
Перем ny, nx;
После объявления переменных со счетчиком направления Напр, новых координат ny и nx выполняется проверка завершения вычислений, и, когда был получен последний ход коня, происходит успешное завершение:
Если Шаг > NN Тогда
Возврат Истина;
КонецЕсли;
Вызовом функции ЛучшийХод(y, x) определяются один из лучших по эвристике ходов и новые координаты для него:
Напр = ЛучшийХод(y, x);
ny = y + dy[Напр];
nx = x + dx[Напр];
После проверки возможности хода этот ход осуществляется и находится решение задачи на новом шаге с новыми координатами коня. В случае его успешного нахождения возвращается Истина, иначе ход отменяется.
Если МожноХодить(ny, nx) Тогда
Доска[ny][nx] = Шаг;
Если Решить(Шаг + 1, ny, nx) Тогда
Возврат Истина;
Иначе
Доска[ny][nx] = 0;
КонецЕсли;
КонецЕсли;
Такая последовательность операторов была включена для возможности упрощенного отказа от эвристики и перехода программного кода к полному перебору. Если предыдущие расчеты не привели к появлению решения, то возвращается Ложь:
Возврат Ложь;
КонецФункции
Процедура Главная() обеспечивает последовательность счета начиная с инициализации, задания начального хода коня. Если для следующего хода получается решение, то доска отображается, иначе сообщается об отсутствии решений:
Процедура Главная()
Инициализация();
Доска[0][0] = 1;
Если Решить(2, 0, 0) Тогда
ПечатьДоски();
Иначе
Сообщить("Нет решений.");
КонецЕсли;
КонецПроцедуры
Затем начинаются вычисления:
Главная();
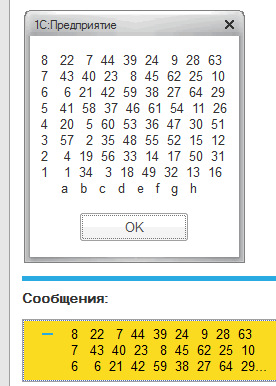
В листингах приводятся исходный текст программы полностью и результаты ее работы (доступны на сайте журнала samag.ru), на иллюстрации – фрагмент окна функционирующей системы (см. рис. 1).
Рисунок 1. Результат работы программы
В результате получена программа на языке 1С для модуля управляемого приложения. Единственная задача для этой программы – поиск решения известной головоломки о ходе коня. Ее рассмотрение позволит прояснить типичные практические ситуации для операторов и функций 1С, как для методов поиска решения, так и для обыкновенных задач обработки информации.
- Вирт Н. Алгоритмы + структуры данных = программы / Н. Вирт. – М.: Мир, 1985. – 406 с.
- Knight’s tour – Rosetta Code. Режим доступа – http://rosettacode.org/wiki/Knight’s_tour.
Ключевые слова: 1С, алгоритм с возвратом, задача о ходе коня.
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
