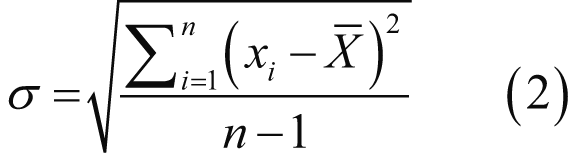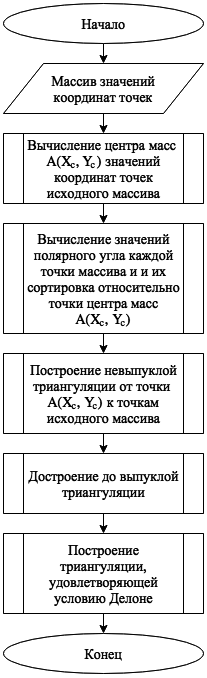
 |
|
|
|
Экспериментальные исследования модифицированного алгоритма триангуляции Делоне
Экспериментальные исследования Приведены результаты экспериментальных численных исследований модифицированного алгоритма триангуляции Делоне, обладающего высоким быстродействием и низкой ресурсоемкостью. Анализ результатов машинных экспериментов подтвердил практическую значимость и целесообразность применения модификации алгоритма для моделирования трехмерных фрактальных объектов виртуальной реальности. Эксперименты проводились в два этапа: подготовительный, вкотором организовалась генерация уникальных точек на заданном диапазоне значений координат, и второй, на котором проводилось исследование зависимости времени построения триангуляции Делоне от количества входных точек, полученных на предыдущем этапе эксперимента. Входные данные для экспериментальных исследований представлены в виде диапазона количества точек [104; 106] с шагом 103, который определяется особенностью отображения объекта с практически приемлемой степенью детализации. Полученные результаты численных экспериментов были подвергнуты дальнейшей обработке путем исключения величин, отклонение которых от среднего значения превышает утроенное стандартное отклонение. Анализ обработанных результатов численных экспериментов показал, что для входного набора данных, не превышающего 3 * 105 точек, модифицированный алгоритм триангуляции Делоне удовлетворяет требованиям реального времени. Предложено дальнейшее направление развития алгоритма путем замены этапа сортировки процедурой динамического вычисления относительных координат текущей точки. Программная реализация модифицированного алгоритма триангуляции Делоне выполнена на языке программирования Python третьей версии при помощи развитых интегрируемых библиотек, таких как matplolib, numpy и scipy, предназначенных для выполнения научных и инженерных расчетов с последующей визуализацией результатов Введение Триангуляция [7] является одним из основных этапов построения трехмерных объектов в области машинной графики [4]. Особую практическую актуальность данная процедура приобретает в моделировании динамических фрактальных объектов с заданной степенью детализации. В таких задачах основополагающим этапом становится построение триангуляции, удовлетворяющей требованиям режима реального времени [5] и специфики «степени правильности» [6, 7]построения треугольников. Алгоритмы триангуляции Делоне решают задачу построения треугольников, удовлетворяющих «степени правильности», но, как показано в [8], не удовлетворяют требованиям режима реального времени. В [8] предложен модифицированный алгоритм триангуляции Делоне, удовлетворяющий требованиям высокого быстродействия и низкой ресурсоемкости. Для подтверждения работоспособности и оценки алгоритмической сложности разработанного в [8] модифицированного веерного двухпроходного алгоритматриангуляции Делоне проведен ряд численных экспериментов, анализ результатов которых приведен ниже. Модифицированный веерный алгоритм триангуляции Делоне Схема модифицированного веерного алгоритма триангуляции Делоне [8] представлена на рис. 1.
Рисунок 1. Схема модифицированного веерного алгоритма триангуляции Делоне Этапы сортировки и построения триангуляции до выпуклой являются наиболее ресурсоемкими и представляют особый практический интерес в представленной схеме. В качестве алгоритма сортировки выбран алгоритм слиянием [2], а в качестве алгоритма построения выпуклой триангуляции – алгоритм Грэхема [9]. Указанные алгоритмы являются наиболее предпочтительными в практическом аспекте среди своих представителей [1, 2], т.к. их реализации занимают приемлемое время О(NlnN). Экспериментальные исследования Исследования проводились на аппаратной платформе со следующими характеристиками:
Программная реализация алгоритма выполнена на языке программирования Python третьей версии [11], что обусловлено наличием развитой интегрируемой библиотеки [10], а также возможностью реализации гибкого тестирования, отладки и диагностики программы. Входные данные для экспериментальных исследований представлены последовательностью значений от 104 точек до 106 точек с шагом 103 что представляет собой серию из ста реализаций вычислительных экспериментов. Указанный диапазон точек определяется особенностью отображения объекта с практически приемлемой степенью детализации [4]. Эксперименты проводились в два этапа.
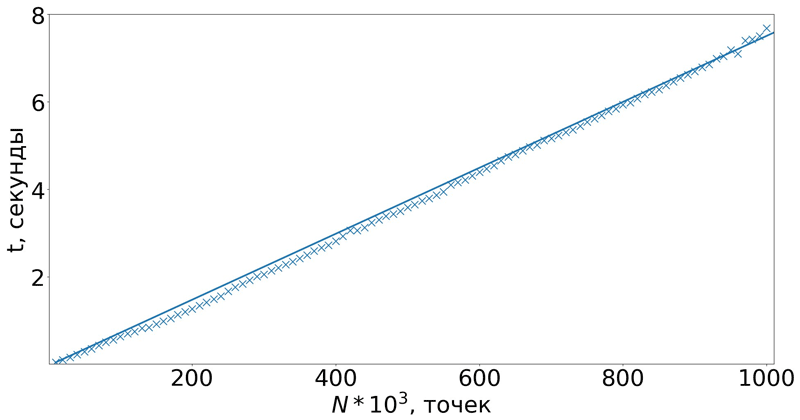
Полученные результаты численных экспериментов были подвергнуты дальнейшей обработке в целях выявления достоверности временной зависимости. Для этого применен следующий набор вычислений: 1. Вычисление среднего значения измерительной величины согласно формуле (1):
где x1+x2+...+xn – значения временных характеристик эксперимента; n – количество временных характеристик эксперимента. 2. Определение значения стандартного отклонения результатов, характеризующее разброс относительно среднего значения, согласно формуле (2):
3. Исключение величин, отклонение которых от среднего значения превышает утроенное стандартное отклонение, согласно данным [3]. Исследование зависимости времени построения триангуляции Делоне от количества входных точек Обработанные результаты проведенных экспериментальных исследований зависимости времени построения триангуляции Делоне от количества входных точек представлены на рис. 2.
Рисунок 2. Зависимость времени построения триангуляции Делоне от количества входных точек Задача построения трехмерных динамических объектов с заданной степенью детализации в режиме реального времени характеризуется временными значениями, не превышающими двух секунд [4]. Следовательно, особый практический интерес возникает к результатам, время реализации которых удовлетворяет данному временному интервалу. Из представленных на рис. 2 зависимостей видно, что на наборе входных данных, не превышающем 3 * 105 точек, время выполнения алгоритма удовлетворяет вышеуказанным требованиям быстродействия. При увеличении количества используемых точек триангуляции (3 * 105 и более) исследованная модификация веерного алгоритма триангуляции Делоне требует дальнейшего развития. Так как этапы сортировки и построения триангуляции до выпуклой являются наиболее ресурсоемкими, то именно они подлежат модификации. Предлагается заменить этап сортировки на процедуру динамического вычисления координат точки относительно соседних точек. Это позволит существенно уменьшить время построения триангуляции, при этом характеристика временной сложности приобретает вид О(N) вместо О(NlnN). Выводы Проведенные численные экспериментальные исследования модифицированного веерного алгоритма триангуляции Делоне подтвердили работоспособность разработанного алгоритмического обеспечения и его практически приемлемое быстродействие. Анализ результатов численных экспериментов показал, что для входного набора данных, не превышающего 3 * 105 точек, модифицированный алгоритм удовлетворяет требованиям реального времени. Предложено дальнейшее направление развития алгоритма путем замены этапа сортировки процедурой динамического вычисления относительных координат текущей точки.
Ключевые слова: виртуальная реальность, триангуляция на заданном массиве точек, триангуляция Делоне, построение динамических трехмерных фрактальных объектов. Experimental research of the modified Delaunay’s triangulation algorithm Teplov A.A., Bachelor, MSTU Bauman, Department of "Software and Information Technologies", Moscow, teploff.a@mail.ru Maikov K.A., Doctor of Technical Sciences, Professor, MSTU Bauman, Department of "Software and Information Technologies", Moscow, maikov@bmstu.ru Abstract: The results of experimental numerical researches of the modified Delaunay’s triangulation algorithm with high performance and low resource consumption are described in this article. The practical significance and expediency of applying the modification of the algorithm have been confirmed by the computer experiments results for modeling three-dimensional fractal objects of virtual reality. The experiments were conducted in the two stages: the generation of the unique points on a given range of coordinate values was in the first one; the research of the time dependence of the modeling Delaunay’s triangulation on the number of input points, which was obtained at the previous experiment stage, was in the second one. Input data for the experimental researches are presented as a range of points array with step of , which is determined by the feature of displaying three-dimensional object with a practically acceptable degree of detail. The results of numerical experiments have been subjected to further interventions by excluding values which exceed the tripled standard deviation. The analysis of numerical experiments shows that the modified Delaunay’s triangulation algorithm satisfies real-time requirements on the input data set. A further direction of the algorithm development is proposed by replacing the sorting step with the procedure of dynamic calculation of the points locations. The software implementation of the modified Delaunay’s triangulation algorithm was performed in the Python programming language of the third version. There were used developed integrable libraries such as: matplotlib, numpy and scipy, each of which had its own particular importance. Numpy and scipy were intended for calculate the time dependence the modified Delaunay’s triangulation algorithm. Matplotlib was intended for visualization of results. Keywords: virtual reality; triangulation on a given cell array, Delaunay’s trian-gulation, building of dynamic three-dimensional objects. |
ТЕПЛОВ А.А., бакалавр, МГТУ имени Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии», Москва, 
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
