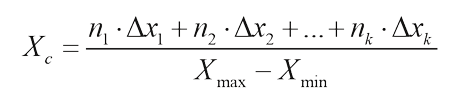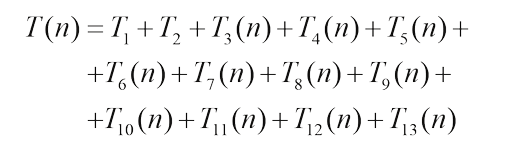Модифицированный алгоритм триангуляции Делоне

 ТЕПЛОВ А.А., бакалавр, МГТУ имени Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии», Москва, teploff.a@mail.ru

 МАЙКОВ К.А., д.т.н., профессор, МГТУ имени Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии», Москва, maikov@bmstu.ru

Модифицированный алгоритм
триангуляции Делоне

Приведены результаты сравнительного анализа методов триангуляции Делоне, обладающих высоким быстродействием и низкой ресурсоемкостью. Обосновывается выбор прототипа для последующей модернизации применительно кпостроению динамических трехмерных объектов в реальном времени с практически необходимой степенью детализации. Предложен алгоритм интервального разбиения массива точек триангуляции в соответствии с плотностью распределения, позволяющий избежать ошибок при аппаратной реализации. Проведен анализ предложенного модифицированного алгоритма триангуляции Делоне

Введение

Одним из этапов, определяющих ресурсоемкость построения динамических 3D объектов с заданной степенью детализации, является триангуляция [3, 4]. На практике возникает необходимость определения прототипа метода триангуляции, удовлетворяющего требованию высокого быстродействия и низкой ресурсоемкости с последующей модификацией для конкретного класса задач.

Постановка решаемых задач

Ряд практических задач характеризуется необходимостью моделирования 3D объектов, описанных соответствующим набором точек с неизвестным законом распределения. Примером подобных задач является моделирование горной гряды или сложных и нерегулярных поверхностных структур, значения высот которых заранее получены средствами дистанционного зондирования. В этом случае необходимо произвести триангуляцию на исходном наборе точек, обеспечивающую наибольшую «степень правильности» треугольников, для которой характерно исключение построения «тонких» треугольников [6] с минимальным значением суммы радиусов описанных окружностей.

Проблема «степени правильности» треугольников решается триангуляцией, удовлетворяющей условию Делоне [3].

Известные алгоритмы триангуляции Делоне можно разделить на следующие четыре категории [6]: итеративные алгоритмы, алгоритмы слияния, двухпроходные алгоритмы и пошаговые; основные особенности указанных алгоритмов рассматриваются ниже.

Итеративные алгоритмы построения триангуляции Делоне

В итеративных алгоритмах реализуется последовательное добавление точек в частично построенную триангуляцию Делоне [4]. Трудоемкость итеративных алгоритмов Делоне определяется как O(N2) [6], а для случая равномерного распределения точек – O(N) [6]. Недостатками итеративных алгоритмов Делоне являются большое число итеративных циклов, зависимость алгоритма сортировки от структуры исходных данных, а также необходимость проверки на условие Делоне в каждом цикле. Преимущества итеративных алгоритмов Делоне – простота реализации и высокое быстродействие выбора эффективного алгоритма сортировки, основывающегося на определенном наборе входных данных [4, 8].

Алгоритмы построения триангуляции Делоне слиянием

Алгоритмы слияния реализуют разбиение исходного множества точек на ряд подмножеств, в которых производится построение триангуляций с последующим объединением ряда решений [6]. Трудоемкость алгоритмов слияния составляет всреднем O(N) [6]. Алгоритмам слияния свойственна избыточность, определяемая необходимостью построения выпуклых областей для «узких» полос [6], а следовательно, формированием длинных, «узких» треугольников [6], перестраиваемых при слиянии. Алгоритмы слияния обладают высоким быстродействием, что обуславливает их практическое преимущество.

Двухпроходные алгоритмы построения триангуляции Делоне

Преимущественная особенность двухпроходных алгоритмов состоит в том, что на первом цикле строится некоторая триангуляция без учета условия Делоне, которая на втором этапе модифицируется согласно условию Делоне [6]. Трудоемкость двухпроходных алгоритмов составляет в среднем O(N) [6], а в наименее благоприятном случае – O(N²) [6]. Недостатком двухпроходных алгоритмов Делоне является необходимость в большом количестве сортировок длякаждой полосы. В то же время данный алгоритм характеризуется высоким быстродействием, т.к. очередной треугольник, попадающий в триангуляцию, не подвергается проверке на удовлетворение условию Делоне, требующему значительных аппаратных ресурсов.

Пошаговые алгоритмы построения триангуляции Делоне

Алгоритмы пошагового построения реализуют лишь треугольники, удовлетворяющие условию Делоне в конечной триангуляции, а поэтому не требуют перестроения [6]. При большой концентрации точек применение пошагового клеточного алгоритма является нецелесообразным. Трудоемкость данного алгоритма в среднем составляет O(N), а в худшем случае – O(N²).

Выбор прототипа для модификации триангуляции Делоне

Практические особенности задачи построения динамических 3D-объектов в реальном времени определяют такие требования к алгоритмам триангуляции Делоне, как высокое быстродействие и низкая ресурсоемкость. Как следует изприведенных выше результатов анализа, рассмотренные алгоритмы не удовлетворяют в полной мере этим требованиям. Поэтому возникает необходимость построения алгоритма, который не зависит от разбиения области триангуляции напримитивы, содержащие точки самой триангуляции, и не требует проверки условия Делоне на каждой итерации добавления текущего треугольника в исходную триангуляцию.

Из приведенных выше результатов сравнительного анализа следует, что двухпроходные алгоритмы триангуляции Делоне, в частности двухпроходной веерный алгоритм [4], лишь частично удовлетворяют критериям высокого быстродействия и низкой ресурсоемкости.

Однако алгоритмы данного типа нуждаются в модификации в целях повышения быстродействия применимо к задачам реального времени. Двухпроходной веерный алгоритм избыточен в определении центра масс точек. Определяя координату точки центр масс по OX или OY, при большом количестве точек нецелесообразно вычислять значение среднего арифметического, и при больших значениях координат точек может произойти переполнение данных, что повлечет за собой ошибку или сбой программы. Поэтому целесообразно все значения точек триангуляции разделить на интервалы по оси X на Δх₁, Δх₂, Δх₃ ... Δх_n и по оси Y на Δy₁, Δy₂, Δy₃ ... Δy_n. Также необходимо определить количество точек, принадлежащих соответствующим интервалам по осям X и Y. Результирующие формулы получения центра координат масс точек имеют следующий вид:

для координаты х_c

(1)

где:

• х_c – x-координата точки центра масс;
• n_i – количество точек на i-м интервале;
• Δх_i – i-й интервал на оси X;
• X_max – максимальное значение по оси X среди всех точек триангуляции;
• X_min – минимальное значение по оси X среди всех точек триангуляции;

для координаты y_c

(2)

где:

• y_c – y-координата точки центра масс;
• n_i – количество точек на i-м интервале;
• Δy_i – i-й интервал на оси Y;
• Y_max – максимальное значение по оси Y среди всех точек триангуляции;
• Y_min – минимальное значение по оси Y среди всех точек триангуляции.

Последующие этапы триангуляции реализуются согласно классическому веерному алгоритму [4]. Схема разработанного модифицированного веерного алгоритма триангуляции Делоне представлена на рис. 1.

Рисунок 1. Схема модифицированного веерного алгоритма триангуляции Делоне

Рисунок 2. Схема определения значений интервалов по оси X

Рисунок 3. Схема определения значений полярного угла для исходного массива координат точек

Рисунок 4. Схема построения ребра, соединяющего точки исходного массива

Наиболее трудоемкими этапами в представленной схеме являются этапы сортировки и построения триангуляции до выпуклой. В качестве алгоритма сортировки был выбран алгоритм слияния [2], а в качестве алгоритма построения выпуклой триангуляции – алгоритм Грэхема [7]. Оба алгоритма работают за приемлемое время и являются наиболее предпочтительными в практическом аспекте среди своих представителей.

Анализ модифицированного веерного алгоритма триангуляции Делоне

Из приведенной на рис. 1 схемы видно, что значение времени построения триангуляции модифицируемым веерным алгоритмом определяется выражением:

(3)

где:

• T₁,T₂ – значения времени вычислений оптимального числа интервалов по осям X и Y соответственно;
• T₃,T₄ – значения времени вычислений X_min и X_max соответственно;
• T₅,T₆ – значения времени вычислений Y_min и Y_max соответственно;
• T₇,T₈ – значения времени вычислений величин интервалов по осям X и Y соответственно;
• T₉ – значение времени вычисления величин полярного угла каждой точки массива относительно точки A(X_c,Y_c);
• T₁₀ – значение времени сортировки слиянием [2] всех точек по полярному углу относительно точки A(X_c,Y_c);
• T₁₁ – значение времени построения ребра от каждой точки массива к точке A(X_c,Y_c);
• T₁₂ – значение времени достроения триангуляции до выпуклой;
• T₁₃ – значение времени перестроения триангуляции, удовлетворяющей условию Делоне;
• n – массив значений координат точек.

Рассмотрим каждую временную зависимость отдельно.

При определении оптимального числа интервалов по оси X и Y, воспользуемся правилом Стерджеса [9], согласно которому количество интервалов n определяется как:

,

где:

• N – общее число наблюдений величины;
• [x] – целая часть числа x.

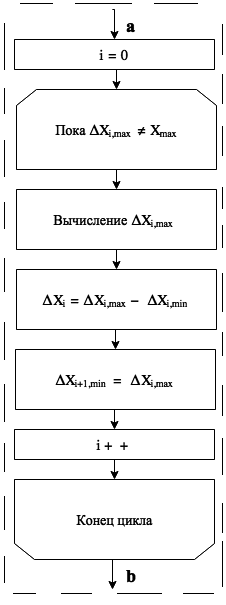
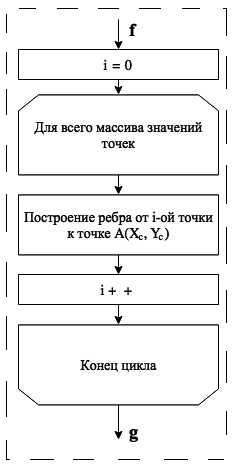
Очевидно, что временные зависимости T₁ и T₂ имеют константные представления c₁ и c₂.

На этапах определения значений X_min, X_max, Y_min, Y_max псевдокод будет выглядеть следующим образом:

Xmin ← M[0]

for i ← 1 to lenght(M) – 1

    if Xmin › M[i]

       Xmin ← M[i]

Xmax ← M[0]

for i ← 1 to lenght(M) – 1

    if Xmax < M[i]

       Xmax ← M[i]

Ymin ← M[0]

for i ← 1 to lenght(M) – 1

    if Ymin › M[i]

       Ymin ← M[i]

Ymax ← M[0]

for i ← 1 to lenght(M) – 1

    if Ymax < M[i]

       Ymax ← M[i]

Из вышеуказанного псевдокода отчетливо видно, что время нахождения максимального или минимального значения величин x или y имеет линейную зависимость O(N), следовательно, T₃(n), T₄(n),T₅(n),T₆(n), имеют временную характеристику O(N) соответственно.

Схема определения значений интервалов по оси X представлена на рис. 2.

Из выше представленной схемы также видна линейная временная зависимость O(N), т.к. в определении величин участвует весь набор координат значений массива точек. Схема определения величин интервалов по оси Y имеет аналогичную структуру и временные характеристики, следовательно, временная зависимость для T₇(n) и T₈(n) имеет вид O(N).

Схема определения значений полярного угла для исходного массива точек представлена на рис. 3.

В виде псевдокода данная схема будет выглядеть следующим образом:

for points to points

    # Если точка лежит на оси координат между I и IV четвертями

    if point.x ≥ Xc and point.y = Yc

        point.angle ← 0

    # Если точка лежит строго в I четверти

    else if point.x > Xc and point.y > Yc

        foundation ← |point.x – Xc|

        perpendicular ← |point.y – Yc|

        point.angle ← arctg(perpendicular/foundation)

    # Если точка лежит на оси координат между I и II четвертями

    else if point.x = Xc and point.y > Yc

        point.angle ← p/2

    # Если точка лежит строго в II четверти

    else if point.x < Xc and point.y > Yc

        foundation ← |point.y – Yc|

        perpendicular ← |point.x – Xc|

        point.angle ← p/2 + arctg(perpendicular/foundation)

    # Если точка лежит на оси координат между II и III четвертями

    if point.x < Xc and point.y = Yc

        point.angle ← p

    # Если точка лежит строго в III четверти

    if point.x < Xc and point.y > Yc

        foundation ← |point.x – Xc|

        perpendicular ← |point.y – Yc|

        point.angle ← p + arctg(perpendicular/foundation)

    # Если точка лежит на оси координат между III и IV четвертями

    if point.x = Xc and point.y < Yc

        point.angle ← 3p/2

    # Если точка лежит строго в IV четверти

    if point.x > Xc and point.y < Yc

        foundation ← |point.y – Yc|

        perpendicular ← |point.x – Xc|

        point.angle ← 3p/2 + arctg(perpendicular/foundation)

Очевидно, что временная характеристика определения значений полярного угла для исходного массива координат точек имеет вид O(N), следовательно, T₉(n) = O(N).

Как показано в [2], сортировка слиянием имеет временную зависимость вида O(N), следовательно, T₁₀(n) = O(NlnN).

Схема построения ребра, соединяющего точки исходного массива, представлена на рис. 4.

Псевдокод вышеуказанной схемы будет иметь вид:

for i ← 0 to length(Points) – 1

    draw(Xc,Yc,Points[i].x, Points[i].y)

Временная характеристика также линейна, следовательно, T₁₁(n) = O(N).

Достроение получившейся триангуляции до выпуклой осуществляется согласно алгоритму Грэхема [1, 7]. В качестве входных данных процедуры выступает множество точек Q, где |Q|≥3. В ней вызывается функция Top(S), которая возвращает точку, находящуюся на вершине стека S, не изменяя при этом его содержимое. Кроме того, используется также функция NextToTop(S), которая возвращает точку, расположенную в стеке S, на одну позицию ниже от верхней точки; стек S при этом не изменяется.

Graham(Q)

    Пусть p₀ – точка из множества Q с минимальной координатой.

    Пусть ‹p₁, p₂,...,p_N› – точки множества Q, отсортированные

    в порядке возрастания полярного угла.

Push(p₀,S)

Push(p₁,S)

for i=2 to N do

    while угол, образованный точками NextToTop(S), Top(S) и pi,

    образуют не левый поворот

        # при движении по ломаной, образованной этими

        # точками, движение осуществляется прямо или вправо

            do Pop(S)

            Push(pi,S)

return S

Время работы процедуры Graham равно O(NlnN), где N=length(Q). Как несложно показать, что циклу while потребуется время O(N), а сортировка полярных углов займет O(NlnN) времени, откуда и следует общая асимптотика процедуры Graham, следовательно, T₁₂(n) = O(NlnN).

Временная характеристика перестроения триангуляции, удовлетворяющей условию Делоне, как показано в [4], имеет линейную зависимость O(N), таким образом, T₁₃(n) = O(N).

Если подставить все найденные временные характеристики в выражение (3), то результирующая временная зависимость будет иметь вид:

T(n) = c₁+c₂+O(N)+O(N)+O(N)+O(N)+O(N)+O(N)+O(N)+ +O(NlnN)+O(N)+O(NlnN)+O(N)

или

T(n) = O(NlnN)

Проведенный теоретический анализ временных характеристик модифицированного алгоритма триангуляции Делоне подтверждает работоспособность и высокое быстродействие предложенного алгоритма.

Выводы

В результате проведенного сравнительного анализа практически востребованных алгоритмов триангуляции Делоне, показано, что рассмотренные методы не удовлетворяют требованиям построения в реальном времени динамических трехмерных объектов с заранее определенной степенью детализации, а следовательно, возникает практическая необходимость их модификации. Предложена модификация веерного двухпроходного алгоритма триангуляции Делоне, функциональной особенностью которого является вычисление значений центра масс массива координат точек триангуляции посредством разбиения массива точек на подмножества по оси X и Y. Произведен анализ временных характеристик модифицированного алгоритма триангуляции Делоне. Указанные вычисления позволяют существенно выиграть в производительности на большом массиве точек при определении координат точки центра масс и избежать переполнения данных, а следовательно, ошибки при программной реализации.

1. Кнут Д.Э. Искусство программирования. Том 1. Основные алгоритмы. – М.: Вильямс, 2008. – 680 с.
2. Кнут Д.Э. Искусство программирования. Том 3. Сортировка и поиск. – М.: Вильямс, 2008. – 800 с.
3. Мандельброт Б. Фрактальная геометрия природы. – М.: Институт компьютерных исследований, 2002. – 656 с.
4. Скворцов А. В. Триангуляция Делоне и ее применение. – Томск: Изд-во Томского университета, 2002. – 128 с.
5. Скворцов А.В. Построение триангуляции Делоне за линейное время. – Томск: Изд-во Томского университета, 1999. – С.120-126.
6. Скворцов А.В., Мирза Н.С. Алгоритмы построения и анализа триангуляции. – Томск: Изд-во Томского университета, 2006. – 168 с.
7. Томас Х. Кормен, Чарльз И. Лейзерон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ, 3-е изд.: Пер. с англ. – М.: Вильямс, 2013. – 1328 с.
8. Шайдуров В.В. Многосеточные методы конечных элементов. – М.: Наука, 1989. – 288 с.
9. Sturges H. (1926). The choice of a class-interval. J. Amer. Statist. Assoc., 21, 65-66.

Ключевые слова: виртуальная реальность, триангуляция на заданном массиве точек, триангуляция Делоне, построение динамических трехмерных объектов.

The modified Delaunay’s triangulation algorithm

Teplov A.A., Bachelor, MSTU Bauman, Department of "Software and Information Technologies", Moscow, teploff.a@mail.ru

Maikov K.A., Doctor of Technical Sciences, Professor, MSTU Bauman, Department of "Software and Information Technologies", Moscow, maikov@bmstu.ru

Abstract: The results of the comparative analysis of the virtually popular methods of the Delaunay’s triangulation with high performance and low resource consumption are described in this article. The choice of the method for further modernization with the aim of building of dynamic 3-D objects in real time with a certain degree of detail is justified. One of the main stages of a fibered the two-pass algorithm of the Delaunay’s triangulation is modified. There is the proposal of the algorithm for the interval partitioning of the cell array of the triangulation in accordance with the density of distribution, allowing to avoid the errors in the hardware implementation.

Keywords: virtual reality, triangulation on a given cell array, Delaunay’s triangulation, building of dynamic 3-D objects.

Комментарии могут оставлять только зарегистрированные пользователи