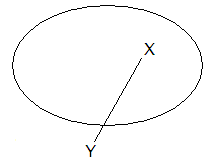|
|
|
|||||||||||||
|
|
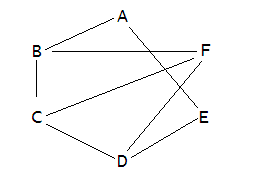
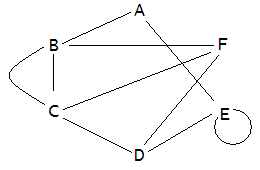
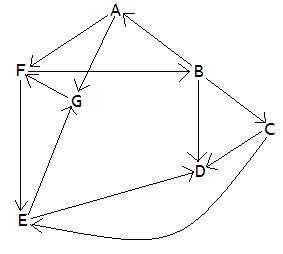
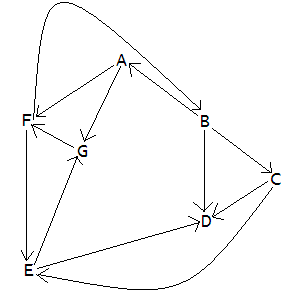
Графы: базовые кирпичики Существует не много математических понятий, имеющих непосредственное отношение к программированию. Что касается графов, то они именно из такой «породы» «Эх вы, серость! Это ж бубль-гум!» Мультфильм «Возвращение блудного попугая» «Союзмультфильм», 1987 Графы обнаруживаются везде: электрические схемы, дорожные сети, расписания задач, структуры химических соединений, социология, транспортные задачи, игры, лингвистика, биология, планирование и, естественно, программирование – вот основные области, в которых методы и результаты теории графов играют ключевую роль. Разумеется, для простых задач, которые люди решают испокон веков, необходимость в этой теории невелика, но есть плохая новость: простых задач уже не осталось, все они давным-давно решены. А те задачи, что есть, слишком сложны и громоздки, чтобы их пытаться решать, руководствуясь лишь здравым смыслом и эмпирическими догадками, – нужны хорошие инструменты. Теория графов – как раз из таких инструментов. И все-таки даже простые задачи становятся яснее, если воспользоваться теорией графов. Вот как раз с такой задачи я и начну. Несерьезно о серьезном Допустим, между шестью участниками (шутки ради, я буду называть их «графоманами») проводится соревнование. Какое именно это соревнование – неважно; это могут быть шахматы, бокс, перетягивание каната, крестики-нолики и т.д. Победитель, как и положено, определяется по результатам соревнований между парами участников. Для отображения хода соревнований и выявления победителя часто используется прямоугольная «сетка», хорошо знакомая любителям футбола или хоккея. Я представлю эту сетку соревнований следующей таблицей (участники обозначены буквами от A до F), в которой дефис означает то, что данная пара графоманов пока еще невстречалась: A - B - - E - B A C - - - F C - B - D - F D - - C - E F E A - - D - - F - B C D - - Думаю, что не ошибусь, утверждая, что работать с такой таблицей не очень удобно. Попробуйте, например, ответить на вопрос: «Каковы общие соперники графоманов A и F?» Атеперь я представлю эту же таблицу чуть иначе. Для этого расставлю на бумаге в произвольном порядке буквы, обозначающие каждого из графоманов, и соединю линиями те из них, между которым игра уже состоялась. Вот что у меня получилось (см. рис. 1). Рисунок 1. Графическое представление сетки соревнований Это же совсем другое дело! Сразу видно, кто с кем уже играл, а кто еще нет (и, кстати, ответом на предыдущий вопрос будет B). Не надо водить пальцем по сетке или по таблице: всепрекрасно видно. Это и есть пример графа. Сразу же замечу, что нет никаких ограничений на форму линий, соединяющих буквы, – они могут быть прямыми (как на рисунке), изогнутыми, волнистыми или пунктирными: важна не форма линии, а ее наличие. Графы бывают разные, а точнее, очень-очень разные. Подробно об этом можно прочитать в книгах по теории графов (которые, сразу же предупреждаю, солидны по объему иобманчиво доступны), но нам не нужно глубоко залезать в математические дебри: почти все, что нам понадобится, можно изложить достаточно кратко. Оставшаяся часть статьи посвящена, во-первых, элементарному введению в теорию графов (которое следует рассматривать скорее как сводку основных понятий), а во-вторых, обсуждению относительно несложных, но очень важных и полезных задач, которые имеют непосредственное отношение к некоторым поставленным ранее проблемам. О терминологии К сожалению, терминологию теории графов нельзя считать устоявшейся: несмотря на почти трехсотлетнюю историю, эта область продолжает бурно развиваться. Например, то, чтоодин автор называет вершиной, другие могут назвать точкой или узлом. Я постараюсь использовать самые распространенные термины, но читатель должен помнить, чтоиспользуемая мной терминология – только один из многочисленных вариантов. Из множества понятий, определений и терминов теории графов я расскажу только о тех, что имеют непосредственное отношение к теме настоящего цикла статей. Графом G называется математический объект, состоящий из множества вершин V = {v1, v2, ...}, часть которых (не обязательно все) соединена ребрами, образующими множество E= {e1, e2, ...}. Иначе говоря, граф G определяется парой множеств: G = (V, E). В нашем примере, V = {A, B, C, ...F} и E = {AB, CF, …}. Если вершины v1 и v2 соединены между собой ребром, то говорят, что это ребро инцидентно данным вершинам (например, ребро CF инцидентно вершинам C и F). Если направление ребра имеет значение (скажем, ребро AB нужно отличать от ребра BA), то граф называется ориентированным (или просто орграфом); в противном случае – неориентированным (граф из примера, разумеется, неориентированный). Каждая точка может быть соединена не одним, а несколькими ребрами (см. рис. 2). Рисунок 2. Пример графа, где каждая точка соединена не одним, а несколькими ребрами Здесь между вершинами B и C проведены два ребра; такие ребра считаются параллельными. Допускается также, чтобы ребро начиналось и заканчивалось в одной и той же вершине (тогда ребро превращается в петлю, например, в вершине E), но мы с вами с такими графами не будем сталкиваться. Граф называется простым, если он не имеет параллельных ребер и петель. Т.о. первый граф – простой, в то время как второй – нет. Последовательность смежных ребер, например (AB, BF, FC, CD), называется маршрутом (часто используется термин «путь»). Если маршрут замкнут, т.е. начинается изаканчивается в одной и той же точке, то такой маршрут называется замкнутым, и граф имеет цикл. Примеры циклов: (BC, CF, FB) или (AB, BC, CD, CE, EA). Каждому ребру графа может быть приписано число – его вес. Такие графы называются взвешенными. Примеры: если граф изображает сеть дорог, то весом ребра можно считать расстояние между населенными пунктами, которым это ребро инцидентно; если граф изображает систему трубопроводов, то весом можно считать пропускную способность каждого из его участков. Обычно вес обозначается его указанием рядом с ребром графа. Если между любой парой вершин графа существует хотя бы один маршрут, то такой граф называется связным; в противном случае такой граф несвязен. Оба предыдущих графа, очевидно, связны. Очень важный тип графов – дерево. Деревом называется связный граф, не имеющий циклов и петель. Их примеров я приводить не буду – они общеизвестны. Вот пока и все, что нам потребуется. Разумеется, это изложение терминологии теории графов не более чем эскиз, но я надеюсь, что, руководствуясь здравым смыслом, читатель сможет достаточно уверенно ориентироваться в этой области. Изображение графов в виде рисунка, изображающего вершины и ребра, обладает, конечно, наглядностью, однако этот способ хорош только для совсем маленьких графов. Но этанаглядность заканчивается, как только граф становится достаточно большим (что обычно и происходит); по мере добавления новых вершин и ребер, изображение графа становится все более и более запутанным. Кроме того, этот способ совершенно непригоден для их компьютерной обработки. Очень и очень быстро в таком рисунке не сможет разобраться никто. Следовательно, необходимы другие способы представления графов. Давайте рассмотрим, какие есть способы представления графов. Представления графов Графы можно представлять в памяти компьютера несколькими способами. Все они эквивалентны друг другу (иначе говоря, имея одно представление, можно перейти к другому). Длянекоторых задач удобно одно представление, но для других – другое. Ниже я расскажу о некоторых, наиболее распространенных представлениях графов. В качестве модели я буду использовать следующий граф (см. рис. 3). Рисунок 3. Модель графа для обучения Этот граф, как нетрудно видеть, является связным, ориентированным и невзвешенным. Кроме того, в нем есть циклы (например, AF-FB-BA или EG-GF-FE), т.е. этот граф – недерево. Матрица смежности Матрица смежности (встречаются также иные названия: «матрица смежностей» и «матрица соединений») – это квадратная матрица (проще говоря, таблица), в которой число строк истолбцов равно числу вершин графа. На математическом языке матрица смежности графа G = (V, E) – это матрица размером |V|*|V|, состоящая из элементов a (i, j), где i и j – соответственно номер строки и столбца. Элемент матрицы a (i, j) = 1, если существует ребро, инцидентное вершинам i и j и направленное от вершины i к вершине j; в противном случае a (i, j) = 0 (см. таблицу 1). Таблица 1. Матрица смежности
Обратите внимание, что из вершины D ни одно ребро не выходит. Это означает, что длина любого маршрута, выходящего из этой вершины равна 0. Я выделил жирным шрифтом вматрице смежности главную диагональ (от левого верхнего к правому нижнему элементам); скоро вы увидите для чего. Теперь мысленно исключим из графа стрелки на концах ребер; граф станет неориентированным. Для такого графа матрица смежности примет вид (см. таблицу 2). Таблица 2. Таблица смежности для неориентированного графа
Присмотревшись, можно заметить, что матрица смежности неориентированного графа симметрична относительно главной диагонали. Это позволяет хранить в памяти компьютера только одну половину матрицы (скажем, верхнюю). При этом возникает небольшая сложность при обращении к элементу матрицы, лежащему ниже главной диагонали, что, правда, элементарно преодолевается следующей проверкой: if i > j then a (j, i) else a (i, j) Для ориентированного графа матрица смежности в общем случае не симметрична относительно главной диагонали и, следовательно, в памяти придется хранить ее целиком. Матрица весов В матрице смежности отображается только факт наличия ребра между двумя вершинами (0 или 1) с учетом его направления. В матрице весов каждому элементу матрицы сопоставлен вес. Если вершины связаны, то в соответствующий элемент матрицы записывается число, равное его весу, если же нет, то в соответствующий элемент – в зависимости от задачи – записывается либо 0, либо ∞ (поскольку ∞ – не число, то обычно используют любое большое число, которое заведомо больше любых возможных весов). Составление матрицы весов я оставляю вам в качестве простого упражнения. Структура смежности В орграфе вершина У считается последователем вершины Х, если существует ребро, направленное из вершины Х в вершину У. Тогда можно описать граф как набор списков. Первый элемент списка – вершина, из которой выходят ребра, а остальные элементы списка – вершины, в которые эти ребра входят. Но, конечно, лучше показать; для нашего графа структура смежности может выглядеть так (для наглядности, первая вершина отделена от списка двоеточием): A: F, G B: A, C, D C: D, E D: E: D, G F: B, E G: F Замечание: Для приверженцев функционального стиля программирования замечу, что структура смежности очень похожа на S-выражения языка программирования Lisp. Первая строка структуры смежности тогда примет вид списка (A (F G)), а четвертая – списка (D). Доступ к элементам списков осуществляется посредством стандартных функций CAR иCDR. Матрица инциденций Матрица инциденций – это матрица, в которой число строк равно числу вершин графа, а число столбцов – числу его ребер. Если эти числа не равны друг другу, то матрица инциденций будет не квадратной, а прямоугольной. Элементы матрицы инциденций определяются следующими правилами:
Для нашего графа матрица инциденций, следовательно, будет выглядеть так (чтобы информация была лучше видна, я оставил нулевые ячейки пустыми) (см. таблицу 3). Таблица 3. Матрица инциденций
Для неориентированного графа все элементы, равные -1, заменяются на 1. Предварительные итоги Мы уже достаточно далеко продвинулись в знакомстве с теорией графов. Теперь самое время закрепить полученные знания на практике. Задача 1 На любом хорошо знакомом вам языке программирования напишите программу для представления графов. Как минимум нужно реализовать матрицу смежности. Но лучше если выреализуете все описанные выше представления (и прежде всего структуру смежности). Это потребуется в следующей задаче. Задача 2 Я показал вам, как один и тот же граф может быть представлен в памяти компьютера многими способами. Следовательно, можно от одного представления переходить к другому. Обозначим представления как МС (матрица смежности), МВ (матрица весов), МИ (матрица инциденций) и СС (структура смежности). Пусть изначально граф представлен МС. Напишите программу, которая осуществляет «прямую» МС → МВ → МИ → СС → МС цепочку преобразований. Ясно, что в конце вы должны получить исходную МС (это, кстати, прекрасный способ проверки того, правильно ли вы все сделали). А теперь доработайте эту программу так, чтобы она осуществляла «обратную» цепочку преобразований, начиная изаканчивая СС. Если вы сумеете решить эти задачи, вы, во-первых, получите бесценный опыт представления в памяти компьютера сложных структур данных, а во-вторых, построите хороший базис для реализации действительно сложных алгоритмов работы с графами. Я ограничусь лишь этими способами представления графов, хотя, конечно, имеются и другие (за дополнительной информацией, как обычно, следует обратиться к специальной литературе). Замечание о деревьях: Не так уж много в программировании структур данных, способных «соперничать» по важности и широте применения, как деревья. Пожалуй, только связные списки (linked list) можно считать более универсальными структурами данных, но о них мы поговорим как-нибудь в другой раз. Вот навскидку примеры деревьев: игровые деревья (шахматы, шашки и т.п.), деревья синтаксического разбора компиляторов, базы данных. Описанные ранее способы представления графов для деревьев мало пригодны, т.к. большинство деревьев – это чрезвычайно динамичные структуры данных; деревья постоянно меняются по глубине и степени «ветвистости». Кроме того, часто требуется не просто дерево, а дерево, упорядоченное по определенным критериям (типичный пример – индексы таблиц базы данных). Поэтому для представления деревьев используются совсем иные способы, но обсуждение этого вопроса выходит за рамки настоящей публикации, и читатель может ознакомиться с ними по соответствующей литературе. Так что в дальнейшем мыбудем обращаться к деревьям лишь время от времени. Полезная формула Оставшуюся часть статьи я посвящу простой, но очень полезной формуле, которую вывел (хотя и не для графов, а для выпуклых многогранников – тетраэдров, кубов и проч.) гениальный математик Леонард Эйлер (1707-1783). Я не буду ни выводить, ни доказывать эту формулу, а просто приведу ее и покажу, чем она может быть полезна. Кстати, именно Эйлера можно считать основателем теории графов и топологии, после того как 1736 году он решил знаменитую «задачу о Кенигсбергских мостах». Однако для начала познакомимся с одной, на первый взгляд совершенно очевидной, теоремой Камилла Жордана (1838-1922). Теорема гласит, что любая замкнутая кривая безсамопересечений на плоскости разбивает эту плоскость на две компоненты (внутреннюю и внешнюю) и является их границей. Доказательство этой теоремы в 1887 году оказалось наудивление неожиданно сложным и вплоть до 1905-го в нем находили погрешности. Проиллюстрируем эту теорему простым примером (см. рис. 4). Рисунок 4. Иллюстрация теоремы Камилла Жордана Здесь эллипс образует замкнутую кривую. Точка X лежит внутри контура эллипса, а точка Y – вне его. Как бы мы ни старались, нам не удастся избавиться от пересечения контура эллипса с отрезком XY. Теперь вернемся к формуле Эйлера. Для этого нам понадобятся еще два важных понятия – плоский граф и грань (или область). Плоским называется граф, который уложен наплоскость так, что все его ребра пересекаются только в вершинах, но не между собой. Если мы обратимся к нашему основному примеру, то увидим, что в нем есть пересечения ребер AG и FB. Однако стоит немного изменить рисунок, и это пересечение исчезает (вспомните, я раньше говорил, что форма линии, изображающей ребро, не имеет значения) (см. рис. 5). Рисунок 5. Преобразование графа для теоремы Камилла Жордана Теперь видно, что граф – плоский. Не все графы можно преобразовать таким образом (т.е. не все графы – плоские), но об этом мы поговорим в свое время. В плоском графе ребра разбивают граф на грани, т.е. замкнутые области, не содержащие внутри себя вершин и ребер. Например, я могу указать грани AFG, FGE, ABDEG и др. Гранью считается и внешняя область той плоскости, в которой расположен граф. А теперь подсчитайте по отдельности число вершин (В), ребер (Р) и граней (Г) нашего графа. У вас должно получиться следующее: В = 7, Р = 12, Г = 7 (напоминаю, что внешняя область, лежащая вне графа, считается гранью). Формула Эйлера утверждает, что для связного плоского графа В – Р + Г = 2 (для нашего примера 7 – 12 + 7 = 2). А теперь обратитесь к самому первому рисунку (граф игры с шестью участниками), преобразуйте граф так, чтобы он стал плоским, подсчитайте числа В, Р и Г и подставьте их в формулу Эйлера. Подсказка: Для этого графа В = 6, Р = 8, Г = 4 Для неплоских графов (т.е. графов, которые невозможно уложить на плоскость так, чтобы никакие два ребра не пересекались) можно показать, что формула Эйлера даст результат, отличный от 2 (я не буду приводить примеров, т.к. это для наших целей нам не нужно, и предлагаю обратиться к библиографии). Вспоминая теорему Жордана, можно поразмышлять о том, как могут выглядеть неплоские графы, но это я оставляю читателю в качестве полезного размышления. Формула Эйлера достойна того, чтобы ее запомнить. Она позволяет сделать некоторые важные заключения о том или ином графе, просто пересчитав его вершины, ребра и грани. Втеории графов формула Эйлера встречается повсеместно, и очень полезно выработать навык обращения с ней: нарисуйте несколько плоских графов и проверьте, как для них она работает. В общем случае определение того, является ли произвольно заданный граф плоским, – непростая задача. Есть ряд критериев, которые позволяют охарактеризовать граф как плоский (см., например, упомянутую в предыдущей статье цикла книгу Ф.Харари). Однако все эти критерии имеют ограниченную практическую ценность, т.к. не дают эффективных алгоритмов для главного вопроса: в какой последовательности необходимо порождать вершины и ребра, чтобы граф оставался планарным? Графы очень «чувствительны» кдобавлению или удалению вершин и ребер: одно-единственное ребро может привести к полному перестроению графа. Эта проблема в программировании называется «определение планарности графов». Существует ряд алгоритмов определения планарности, но об этом мы поговорим позже. Вот в целом и все, что я хотел рассказать в этой статье. Конечно, многое мне пришлось опустить и практически все – упростить. В заключение еще раз настоятельно рекомендую вам решить первую задачу, причем для всех случаев.
|
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 АЛЕКСЕЙ ВТОРНИКОВ, ЗАО КБ «Ростовский Универсальный», ведущий программист,
АЛЕКСЕЙ ВТОРНИКОВ, ЗАО КБ «Ростовский Универсальный», ведущий программист,