|
|
|
|||||||||||||
|
|
Трудный путь наверх Вам нравится решать задачи? Вероятный ответ: «смотря какие». А ведь работа программиста – это как раз решение задач «Потому, что он существует» Мне кажется очевидным, что только решение сложных задач способно поднять профессиональный уровень программиста. Если программист избегает таких задач – это скорее всего говорит о том, что великое ему не по плечу. Конечно, каждый решает сам, к чему стоит стремиться; большинство практически лишено профессиональных амбиций и довольствуется пусть рутинной, но спокойной и стабильной работой. Но некоторым чудакам этого мало. Однажды журналист из The New York Times задал Джорджу Ли Мэллори (английский альпинист, погибший при попытке подняться на Эверест в 1924 году) вопрос: «Зачем вы туда лезете?» Ответ был и простым и гордым: «Потому, что он существует». Упражнения, задачи, проблемы В своем «Искусстве программирования» Дональд Кнут приводит следующее высказывание математика Ричарда Беллмана: «Если вы можете решить задачу, значит, это упражнение; в противном случае это научная проблема». И это действительно так. Простая задача может оказаться почти непреодолимой для новичка, но пустяком для мастера. С другой стороны, действительно сложная задача проскочит мимо сознания дилетанта, но заставит оцепенеть профессионала. Грубо говоря, все задачи можно разделить на три категории:
Первые две категории я далее обсуждать не буду: они – необходимая часть процесса обучения и становления профессионала. Их надо уметь решать, и точка. Может быть, преодолевая отвращение к задачникам, но надо. Лучше поговорим о проблемах. О проблемах Все-таки какие задачи можно считать проблемами? Вероятно, те, что либо еще не решены, либо решены частично, либо решены плохо («плохо» означает, что решение не удовлетворяет требованиям скорости, затратам памяти или предполагает существенные ограничения на объем обрабатываемых данных). Вот, например, древняя настольная игра го (она очень распространена в Китае, Японии и Корее, но достаточно давно в нее успешно играют и европейцы). Игровое поле представляет собой расчерченную на клетки горизонтальными и вертикальными линиями доску (обычно размером 19*19, но можно и меньше). Играют два соперника. Игра заключается в установке фишек (их в го называют «камни») на пересечениях линий. Цель игры – контроль за территорией и пленение вражеских камней. При всей простоте правил – буквально полстраницы – го успешно сопротивляется всем попыткам создать компьютерную программу, играющую хотя бы в силу среднего любителя. Го в отличие от шахмат или шашек пока не поддается счету – в ней эти методы работают плохо. В го есть что-то такое, что никак не вписывается в имеющиеся методы решения игровых задач. Разумеется, пример с го относится к «высшему пилотажу» и не слишком показателен. Но важно подчеркнуть то, что при решении проблем необходимо привлекать не только технические навыки, но и нечто такое, что называется интеллектом. Вот небольшие примеры, которые иллюстрируют эту мысль. Пример 1: взвешивание монет Имеется восемь монет одинакового достоинства, но одна монета тяжелее других. Кроме того, есть весы с двумя чашами. Какое минимальное число взвешиваний необходимо для того, чтобы найти самую тяжелую монету? Подумайте пару минут, прежде чем читать дальше. Решили? Прекрасно! Подсказки для тех, кто не решил.
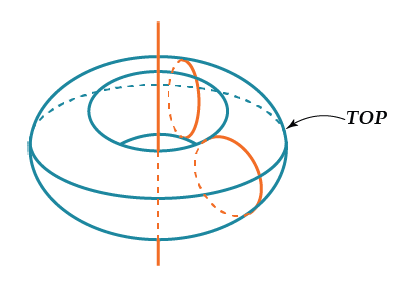
Пример 2: площадь поверхности тора
Тор – это объемная геометрическая фигура в форме бублика. Всем известные примеры – обруч, камера автомобильной шины, пластиковое кольцо детской пирамидки или резиновый эспандер для тренировки мышц запястья и кисти. Некоторое подобие тора легко изготовить из пластилина, теста или глины. А теперь посмотрите внимательно на рисунок тора и ответьте на вопрос: чему равна площадь поверхности тора? Я неоднократно задавал этот вопрос разным людям, в том числе математикам. Многие просто растерянно пожимали плечами и отказывались решать, даже не пытаясь подумать. Математики же часто начинали с того, что тут надо применить математический анализ. Когда я говорил, что задача решается и без этих сложностей, то решение обычно, хотя и не сразу, находили почти все. Подумайте и вы. Решение и просто, и изящно. Помните, я просил внимательно посмотреть на рисунок? Разрежьте тор вдоль одной из поперечных (малых) окружностей и распрямите то, что получилось в трубку. А теперь разрежьте полученную трубку вдоль образующей (большая синяя окружность на рисунке). Что получится? Правильно – прямоугольник! Длина каждой стороны этого прямоугольника равна длине соответствующей окружности. А дальше – элементарная арифметика (окончательный ответ я не привожу, найдите его сами, а потом сверьтесь, например, в интернете). Являются ли приведенные примеры проблемами? Для кого как. Но в обоих случаях задачи были из разряда нестандартных; для их решения потребовалось выйти (хотя и недалеко) за пределы привычного. Три задачи Теперь давайте рассмотрим еще три задачи. Первую мы решим вместе, а вот вторая и третья останутся без решений – их решение легко отыскать в интернете. Кроме того, мне не хочется лишать читателя удовольствия подумать самостоятельно. Из пустого в порожнее Все, вероятно, сталкивались с задачами такого типа: Имеется два сосуда; емкость первого – 7 л, емкость второго – 5 л. Кроме того, есть неисчерпаемый источник воды (например, река или море). Нужно отмерить ровно 1 л воды. Подумайте несколько минут. Я почти уверен, что вам удалось решить эту задачу. На всякий случай вот решение:
А теперь главный вопрос: какой минимальный объем воды можно отмерить, имея два сосуда разной емкости (емкости, разумеется, должны выражаться целыми числами)? Например, какой минимальный объем воды можно отмерить, имея сосуды на 8 и 5 л и т.д.? Вернемся к решению задачи с сосудами на 5 и 7 л. Подсчитаем количество наполнений каждого из сосудов. Должно получиться вот что: сосуд на 7 л наполнялся три раза, а сосуд на 5 л наполнялся четыре раза. Почти очевидным становится уравнение: (7*3) – (5*4) = 1 или в более общем виде: (A*M) – (B*N) = 1 где A и B – емкости сосудов, а M и N – количество наполнений каждого из них. Уравнения такого вида называются «уравнениями первого порядка с двумя неизвестными». Для сосудов на A = 8 л и B = 5 л уравнение приобретает вид: (8*M) – (5*N) = 1 Можно ли подобрать такие M и N, чтобы уравнение стало истинным? Можно: M = 2, N = 3 (16 – 15 = 1). А что для сосудов на 9 и 5 л? Ответ: M = 4, N = 7. А теперь пусть A = 4 л и B = 2 л. Нужно решить уравнение: (4*M) – (2*N) = 1 Получилось (напоминаем, решение должно быть только целочисленным)? Нет, не получилось. Вот два литра можно, а один – никак не получается. Аналогично для сосудов на 6 и 4 л. Что-то знакомое, но вот что... Присмотритесь повнимательнее к парам (7, 5), (8, 5), (9, 5), для которых можно отмерить точно 1 л воды. Оба числа в каждой паре взаимно просты, т.е. имеют общим делителем единственное число – как раз ту самую единицу. Более того, эта единица – наибольший общий делитель. Для пар (4, 2) и (6, 4) наибольший общий делитель равен 2. Поэтому с их помощью 2 л отмерить можно, а вот 1 л – никак. Все становится на свои места, и благодарить за это Напоследок, простой вопрос для самопроверки: чему равен НОД (6501, 528), т.е какое минимальное количество воды можно отмерить, имея сосуды соответствующих объемов? Выше мы несколько раз встретились с уравнениями первого порядка с двумя неизвестными. Задача для любознательных: напишите программу, подбирающую пару чисел M и N в уравнении (A*M) – (B*N) = 1 при заданных A и B. Если такой пары подобрать нельзя, то программа должна вывести сообщение и остановиться. Задача о старушках Эту задачу в детстве предложил учитель математики своему ученику – нашему соотечественнику, выдающемуся математику В.И. Арнольду (1937-2010). Поверьте, это настоящий шедевр. Из пункта A в пункт B и из пункта B в пункт A одновременно на рассвете и по одной дороге вышли навстречу друг другу две старушки. Они встретились в полдень, но не остановились, а продолжили свой путь. Первая старушка пришла в пункт B в 16 часов, а вторая пришла в пункт A в 21 час. В котором часу был рассвет (скорости каждой из старушек оставались постоянными в течение всего пути)? Задача о старушках по форме напоминает унылые школьные задачки о трубах, бассейнах и землекопах, но, однако, она далеко не так проста, как может показаться. Если вы справитесь с задачей, скажем, за час, то поздравьте себя – у вас, несомненно, способности к математике (кстати, по признанию В.И. Арнольда, он смог решить задачу только после многих часов упорных размышлений, правда, тогда ему было всего около 12 лет). Задача Иосифа Следующая задача носит несколько названий (из которых самое известное «задача Иосифа») и несколько модификаций. Вот один из вариантов: Согласно древней легенде, отряд из 40 израильтян попал в окружение к римлянам. Не желая сдаваться врагу, воины стали в круг и договорились последовательно убивать каждого третьего воина, пока в живых не останутся два последних. Эти последние должны будут убить друг друга. Иосиф быстро рассчитал, какое место ему нужно занять в круге. После того как остались два воина (один из них – Иосиф), они сдались в плен (благодаря чему, собственно, история и стала известна). На какое место должен был стать Иосиф, чтобы выжить? Задачу нужно постараться решить в общем виде, т.е. не ограничиваясь 40 воинами и умерщвлением каждого третьего. Буду откровенен: это весьма сложная задача, хотя рекурсивная программа, решающая эту задачу, на удивление коротка. Я приведу эту программу (на Java) без комментариев, но лучше не надейтесь, что это вам как-то поможет – скорее наоборот: public class Josephus { public Josephus () { int q = 40, delta = 3; System.out.println (josephus (q, delta)); } int josephus (int n, int k) { return josephus (n, k, 1); } int josephus (int n, int k, int startingPoint) { if (n == 1) return 1; int newSp = (startingPoint + k - 2) % n + 1; int survivor = josephus (n - 1, k, newSp); if (survivor < newSp) { return survivor; } else { return survivor + 1; } } public static void main (String [] args) { new Josephus (); } } В целочисленных переменных q и delta хранятся, соответственно, общее число воинов и порядок их пересчета; можете заменить их другими значениями для проверки своего решения, если, конечно, вы его найдете. Очевидно, что две последние задачи, действительно, сложные. Если вам эти задачи незнакомы, то вы можете потратить много времени, пытаясь их решить. Так что, с моей точки зрения, это, действительно, проблемы. Чтобы их решить, придется хорошенько подумать. Что дальше? Конечно, не стоило бы приводить все эти задачи и проблемы просто так, без далеко идущих целей. Я просто хотел подготовить читателя к тому, что в дальнейшем нам встретятся по-настоящему большие и сложные задачи, которые любознательный читатель может попробовать решить – т.е. написать соответствующие программы. Отбирая эти задачи, я ставил своей целью не просто рассказать о тех или иных сложных проблемах. Все эти задачи до единой носят сугубо прикладной характер. Это первое, что их роднит. Второе, что между ними общего, – все они для своего решения требуют привлечения математики. Нет, не пугайтесь – никаких продвинутых разделов вам изучать не придется (хотя, честно говоря, лучше бы с ними познакомиться – здесь найдется немало интересного и удивительного). Вся математика, которая потребуется, не выходит за пределы школьного курса алгебры. Но, как вы, наверное, уже поняли, даже школьная математика может оказаться коварной. Вот примерный список задач (нет, наверное, все-таки проблем), которые мы рассмотрим в следующих публикациях (хотя и необязательно в этой же последовательности):
Возможно, будут и другие задачи, но пока я остановился на этом списке. Повторюсь, что все без исключения задачи имеют прикладное значение. В доказательство этого ниже приведено краткое и довольно грубое описание каждой из них. Диаграммы Вороного Это задача определения близости точек на плоскости или в пространстве. Диаграммы Вороного используются в планировании городов, проектировании сложных производств, службах доставки, логистике и прочее, т.е. везде, где нужно оптимизировать доступность, стоимость или время. Мы ограничимся обсуждением диаграмм Вороного на плоскости. Планарность графов Граф – это множество вершин и соединяющих их ребер (дуг, ветвей). Будем рассматривать только графы на плоскости. Граф называется планарным, если никакие два его ребра не пересекаются. Пусть дан произвольный граф (т.е. список вершин и множество соединяющих вершины ребер). Задача: является ли этот граф планарным? Все, вероятно, видели печатные платы. Планарность графов в этом контексте – это поиск решения следующей задачи: можно ли соединить произвольные точки на плате проводником (дорожкой) так, чтобы этот проводник не пересекал других? Если это сделать невозможно, то придется делать либо многослойные платы, либо использовать дополнительные соединительные провода. Практическая задача? Несомненно. Расстояние Левенштейна Даны две строки. Какое минимальное количество преобразований (т.е. вставки, удаления и замены символов) нужно выполнить, чтобы преобразовать одну строку в другую? Помните детскую задачу сделать из мухи слона? Вот примерно об этом и пойдет речь. Сферы использования – поисковые системы, распознавание и исправление текста, биоинформатика. Восстановление изображений Знаете ли вы, что такое японский кроссворд? Ну, разумеется! В японском кроссворде изображения закодированы числами на границах области изображения. Задача играющего – восстановить изображение по этим числам. А как томограф воссоздает изображение, знаете? Входными данными томографа являются данные, полученные от просвечивания тканей и органов тонкими пучками частиц (всякое излучение, в т.ч. рентгеновское, – это согласно квантовой механике и волна, и частица). И хотя японские кроссворды и томографы друг другу не аналогичны, но кое-что общее в них есть. Разве не практическая задача? Куда уж практичнее. Что почитать?
Теория чисел и алгоритм Евклида Многие книги по теории чисел – это устрашающего содержания тексты, до предела насыщенные совершенно зубодробительной математикой, но, к счастью, есть прекрасные введения, которые я с удовольствием рекомендую читателю (книги расположены в порядке возрастания сложности):
Все эти книги неоднократно переиздавались различными издательствами, так что воспользуйтесь теми изданиями, какие найдете. Теория графов Здесь я не буду оригинальничать и просто приведу список некоторых канонических книг:
Давайте пока на этом и остановимся. Вскоре нам предстоит большая, сложная, но интересная работа. И напоследок маленький совет: если будет время и желание, то восстановите в памяти основные понятия теории графов – пригодится!
|
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 АЛЕКСЕЙ ВТОРНИКОВ,
АЛЕКСЕЙ ВТОРНИКОВ,