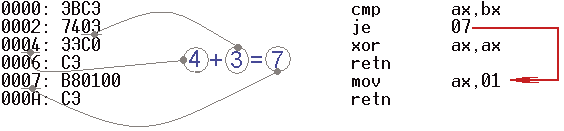|
|
|
|||||||||||||
|
|
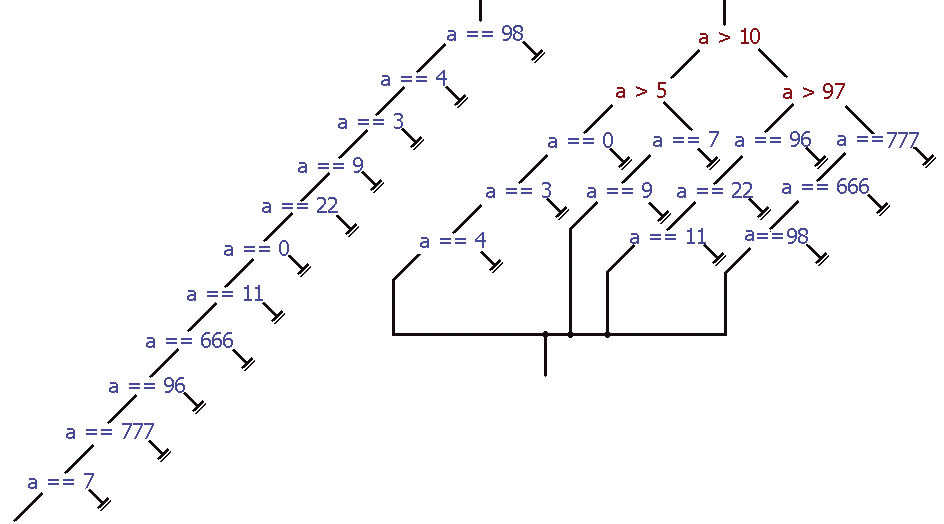
Техника оптимизации под Linux Часть II – ветвления Сегодня мы продолжим сравнение Linux-компиляторов, начатое в прошлом номере журнала, и рассмотрим оптимизацию условных переходов и операторов типа switch. Механизмы их трансформации достаточно многочисленны и разнообразны. За последнее время было предложено множество новых идей, воплощенных в компиляторах GCC 3.3.4 и Intel C++ 8.0 (сокращенно icl), однако древний Microsoft Visual C++ 6.0 (сокращенно msvc) не сдает своих позиций, так что не спешите списывать его в утиль и сдавать на свалку. Оптимизация ветвлений/branch Ветвления (по-английски branch, они же условные/безусловные переходы) относятся к фундаментальным основам любого языка, без которых не обходится ни одна программа. Даже «hello, world!»! Ведь выход из функции main – это тоже ветвление, пусть и неявное (однако ж процессор синтаксисом языка не проведешь!). А сколько ветвлений содержит сама функция printf? А библиотека времени исполнения? Суперскалярные микропроцессоры, построенные по конвейерной архитектуре (а все современные микропроцессоры именно так и устроены), быстрее всего выполняют линейный код и ненавидят ветвления. В лучшем случае они дезориентируют процессор, слегка приостанавливая выполнение программы, в худшем же – полностью очищают конвейер. А на последних Pentium он очень длинный (и с каждой последующей моделью становится все длиннее и длиннее). Быстро его не заполнишь… на это может уйти не одна сотня тактов, что вызовет обвальное падение производительности. Оптимизация переходов дает значительный выигрыш, особенно если они расположены внутри циклов (кстати говоря, циклы – это те же самые переходы), поэтому качество компилятора не в последнюю очередь определяется его умением полностью или частично избавляться от ветвлений. Выравнивание переходов Процессоры, основанные на ядрах Intel P6 и AMD K6, не требуют выравнивания переходов, за исключением того случая, когда целевая инструкция или сама команда перехода расщепляются границей кэш-линейки пополам, в результате чего наблюдается значительное падение производительности. Наибольший ущерб причиняют переходы, находящиеся в циклах с компактным телом и большим уровнем вложения. Чтобы падения производительности не происходило, некоторые компиляторы прибегают к выравниванию, располагая инструкции перехода по кратным адресам и заполняют образующиеся «дыры» незначащими инструкциями, такими как XCHG EAX, EAX (обмен содержимого регистров EAX местами) или MOV EAX, EAX (пересылка содержимого EAX в EAX). Это увеличивает размер кода и несколько снижает его производительность, поэтому бездумное (оно же «агрессивное») выравнивание только вредит. Легко показать, что машинная команда требует выравнивания в тех, и только тех случаях, когда условие: ((addr % cache_len + sizeof(ops)) > cache_len) становится истинным. Здесь: addr – линейный адрес инструкции, cache_len размер кэш-линейки (в зависимости от типа процессора равный 32, 64 или 128 байтам), ops – сама машинная инструкция. Количество выравнивающих байт рассчитывается по формуле: (cache_len - (addr % cache_len)) Именно так поступают все программисты, владеющие Ассемблером, но только не компиляторы! MSVC и icl вообще не выравнивают переходов, а gcc выравнивает целевую инструкцию на фиксированную величину, кратную степени двойки (т.е. 2, 4, 8…), что является крайне неэффективной стратегией, однако даже плохая стратегия все же лучше, чем совсем никакой. Кстати говоря, именно по этой причине, компиляторы msvc и icl генерируют неустойчивый код, точнее код с «плавающей» производительностью, быстродействие которого главным образом зависит от того, расщепляются ли глубоко вложенные переходы или нет. А это в свою очередь зависит от множества трудно прогнозируемых обстоятельств, включающих фазу луны и количество осадков. Учитывая, что средняя длина x86-инструкций составляет 3.5 байта, целесообразнее всего выравнивать переходы по границе четырех байт (ключ -falign-jumps=4 компилятора gcc). Ключ -fno-align-jumps (или эквивалентный ему -falign-jumps=1) отключает выравнивание. Ключ falign-jumps=0 задействует выравнивание по умолчанию, автоматически выбираемое компилятором в зависимости от типа процессора. Листинг 1. Формула для расчета оптимальной кратности выравнивания для процессоров Intel Pentium II и выше if ((addr % cache_len + sizeof(ops)) > cache_len) align = cache_len – (addr % cache_len); Частичное вычисление условий «Летят два крокодила – один квадратный, другой тоже на север», – вот хороший пример техники быстрого булевого вычисления (оно же «частичное вычисление условий», «Partial evaluation of test conditions» или «short-circuiting»). Собственно, ничего «быстрого» в нем нет. Если первое из нескольких условий, связанных оператором AND, ложно (где вы видели квадратных крокодилов?), остальные уже не вычисляются. Соответственно если первое из нескольких условий, связанных оператором OR, истинно, вычислять остальные нет нужды. Это значит, что в выражениях вида (1 || f(x)) или (0 && f(x)) функция f(х) просто не вызывается. И это отнюдь не свойство оптимизатора (как утверждают некоторые рекламные буклеты), а требование языка, без которого ветвления вида: if (x && (y/x)) были бы невозможны, поскольку вычислять значение выражения (y/x) можно тогда и только тогда, когда x=!0, т.е. выражение (x) истинно. В противном случае процессор выбросит исключение и выполнение программы будет остановлено. Поэтому такая стратегия поведения сохраняется даже при отключенном оптимизаторе. Все три рассматриваемых компилятора поддерживают быстрое булевое вычисление. Листинг 2. Если выражение (a == b) истинно, выражение (c == d) уже не проверяется if ((a == b) || (c == d))… Удаление избыточных проверок Небрежное кодирование часто приводит к появлению избыточных или даже заведомо ложных проверок, полностью или частично дублирующих друг друга, например: «if (a > 9) … if (a > 6)…». Очевидно, что вторая проверка лишняя и icl благополучно удаляет ее. Остальные рассматриваемые компиляторы такой способностью не обладают, послушно генерируя следующий код. Листинг 3. Неоптимизированный вариант if (n > 10) a++; else return 0; if (n > 5) a++; else return 0; // избыточная проверка if (n < 2) a++; else return 0; // заведомо ложна проверка Листинг 4. Оптимизированный вариант if (n > 10) a+=2; else return 0; Удаление проверок нулевых указателей Программисты до сих пор не могут определиться, кто должен осуществлять проверку аргументов – вызывающая или вызываемая функция. Многие стандарты кодирования предписывают выполнять такую проверку обеим: Листинг 5. Неоптимизированный вариант f1(int *p) { // проверка №2 (может быть удалена компилятором т.к. ей предшествовала запись по указателю) if (p) return *p+1; else return –1; } f2(int *p) { // проверка №1/запись по указателю if (p) *p = 0x69; else return -1; return f1(p); } Лишние проверки увеличивают размер кода и замедляют его выполнение (особенно если находятся глубоко в цикле), поэтому компилятор gcc поддерживает специальный ключ, fdelete-null-pointer-checks, «вычищающий» их из программы. Вся соль в том, что x86-процессоры (как и большинство других) на аппаратном уровне отслеживают обращения к нулевым указателям, автоматически выбрасывая исключение, если такое обращение действительно произошло. Поэтому, если проверке на «легитимность» указателя предшествует операция чтения/записи по нему, эту проверку можно не выполнять. Рассмотрим, листинг 5. Сначала проходит проверка указателя (проверка №1), потом в него записывается число 0x69, и указатель передается функции f1, выполняющей повторную проверку (проверка №2). Компилятор видит, что вторая проверка осуществляется уже после обращения к указателю (естественно, чтобы он мог это осознать, функция f1 должна быть встроенной или задействован режим глобальной оптимизации) и рассуждает так: если операция присвоения *p = 0x69 проходит успешно и процессор не выбрасывает исключения, то указатель p гарантированно не равен нулю, и в проверке нет никакой нужды. Если же указатель равен нулю, тогда при обращении к нему процессор выбросит исключение и до проверки дело все равно не дойдет. Так зачем же тогда ее выполнять? Компиляторы msvc и icl такой техники оптимизации не поддерживают. Правда, в режиме глобальной оптимизации, icl может удалять несколько подряд идущих проверок (при встраивании функций это происходит достаточно часто), поскольку это является частным случаем техники удаления избыточных проверок, однако ситуацию «проверка/модификация указателя/обращение к указателю/проверка» icl уже не осилит. А вот gcc справляется с ней без труда! Совмещение проверок Совмещение проверок очень похоже на повторное использование подвыражений: если одна и та же проверка присутствует в двух или более местах и отсутствуют паразитные зависимости по данным, все проверки можно объединить в одну: Листинг 6. Неоптимизированный вариант, 2 проверки if (CPU_TYPE == AMD) // проверка x = AMD_f1(y); else x = INTEL_f1(y); … if (CPU_TYPE == AMD) // еще одна проверка a = AMD_f2(b); else a = INTEL_f2(b); Листинг 7. Оптимизированный вариант, только одна проверка if (CPU_TYPE == AMD) // только одна проверка { x = AMD_f1(y); a = AMD_f2(b); } else { x = INTEL_f1(y); a = INTEL_f2(b); } Из всех трех компиляторов совмещать проверки умеет только icl, да и то не всегда. Сокращение длины маршрута Если один условный или безусловный переход указывает на другой безусловный переход, то все три рассматриваемых компилятора автоматически перенаправляют первый целевой адрес на последний, что и демонстрирует следующий пример: Листинг 8. Неоптимизированный вариант goto lab_1 ; // переход к метке lab_1 на безусловный переход к метке lab_2 …. lab_1: goto lab_2 ; // переход к метке lab_2 …. lab_2: Листинг 9. Оптимизированный вариант goto lab_2 ; // сразу переходим к метке lab_2, минуя lab_1 …. lab_1: goto lab_2 ; // переход к метке lab_2 …. lab_2: Разумеется, оператор goto не обязательно должен присутствовать в программном коде в явном виде. Он вполне может быть «растворен» в цикле: Листинг 10. Неоптимизированный вариант while(a) // lab_1: if (!a) goto lab_4 { while(b) // lab_2: if (!b) goto lab_3 /* переход на безусловный переход */ { /* код цикла */ } // goto lab_2 } // lab_3: goto lab_1 // lab_4: После оптимизации этот код будет выглядеть так: Листинг 11. Оптимизированный вариант while(a) // lab_1: if (!a) goto lab_4 { while(b) // lab_2: if (!b) goto lab_1 /* оптимизировано */ { /* код цикла */ } // goto lab_2 } // lab_3: goto lab_1 // lab_4: Аналогичным способом осуществляется и оптимизация условных/безусловных переходов, указывающих на другой условный переход. Вот, посмотрите: Листинг 12. Неоптимизированный вариант jmp lab_1 ; // переход на условный переход … lab_1: jnz lab_2 Листинг 13. Оптимизированный вариант jnz lab_2 ; // оптимизировано … lab_1: jnz lab_2 Заметим, что в силу ограниченной «дальнобойности» (см. врезку «Трансляция кротких условных переходов») условных переходов, в некоторых случаях длину цепочки приходится не только уменьшать, но и увеличивать, прибегая к следующему трюку: Листинг 14. Трансформация условных переходов, до которых процессор не может «дотянуться» jz far_far_away jnz next_lab ———трансформация—————> jmp far_far_away next_lab: Условный или безусловный переход, указывающий на выход из функции, заменяется всеми тремя компиляторами на непосредственный выход из функции, при условии, что код-эпилог достаточно мал и накладные расходы на его дублирование невелики: Листинг 15. Неоптимизированный вариант f(int a, int b) { while(a--) { if (a == b) break; // условный переход на return a; } return a; } Листинг 16. Оптимизированный вариант f(int a, int b) { while(a--) { if (a == b) return a; //непосредственный return a; } return a; } Уменьшение количества ветвлений Все три компилятора просматривают код в поисках условных переходов, перепрыгивающих через безусловные (conditional branches over unconditional branches) и оптимизируют их: инвертируют условный переход, перенацеливая его на адрес безусловного перехода, а сам безусловный переход удаляют, уменьшая тем самым количество ветвлений на единицу: Листинг 17. Неоптимизированный вариант if (x) a=a*2; else goto lab_1; // двойное ветвление if – else b=a+1 lab_1: c=a*10 Листинг 18. Оптимизированный вариант if (!x) goto lab_1; // одинарное ветвление a=a*2; b=a+1; lab_1: c=a*10; Оператор goto не обязательно должен присутствовать в тексте явно, он вполне может быть частью do/while/break/continue. Вот, например: Листинг 19. Неоптимизированный вариант, 2 ветвления while(1) { if (a==0x66) break; // условный переход a=a+rand(); }; // скрытый безусловный переход на начало цикла Листинг 20. Оптимизированный вариант, 1 ветвление (ветвление перед началом цикла не считается, т.к. исполняется всего лишь раз) if (a!=0x66) // «сдирание» одной итерации цикла do{ a=a+rand(); }while(a!=0x66); // инвертируем переход, только одно ветвление Сокращение количества сравнений Процессоры семейства x86 (как и многие другие) обладают одной очень интересной концепцией, которой нет ни в одном языке высокого уровня. Операции вида if (a>b) выполняются в два этапа. Сначала из числа a вычитается число b и состояние вычислительного устройства сохраняется в регистре флагов. Различные комбинации флагов соответствуют различным отношениям чисел и за каждый из них отвечает «свой» условный переход. Например: Листинг 21. Сравнение двух чисел на языке ассемблера cmp eax,ebx // сравниваем eax с ebx, запоминая результат во флагах jl lab_1 // переход, если eax < ebx jg lab_2 // переход, если eax > ebx lab_3: // раз мы здесь, eax == ebx На языках высокого уровня все не так, и операцию сравнения приходится повторять несколько раз подряд, что не способствует ни компактности, ни производительности. Но, может быть, ситуацию исправит оптимизатор? Рассмотрим следующий код: Листинг 22. Сравнение двух чисел на языке высокого уровня if (a < 0x69) printf("b"); if (a > 0x69) printf("g"); if (a == 0x69) printf("e"); Дизассемблирование показывает, что компилятору msvc потребовалось целых два сравнения, а вот icl было достаточно и одного. Компилятор gcc не заметил подвоха и честно выполнил все три сравнения. Избавление от ветвлений Теория утверждает, что любой вычислительный алгоритм можно развернуть в линейную конструкцию, заменив все ветвления математическими операциями (как правило, запутанными и громоздкими). Рассмотрим функцию поиска максимума среди двух целых чисел: «((a>b)?a:b)», для наглядности записанную так: «if (a На Ассемблере это могло бы выглядеть, например, так: Листинг 23. Поиск максимума среди двух целых чисел без использования ветвлений SUB b, a ; отнять от содержимого 'b' значение 'a', записав результат в 'b', если a > b, то процессор установит флаг заема в единицу SBB c, c ; отнять от содержимого 'c' значение 'c' с учетом флага заема, записав результат обратно в 'c' ('c' – временная переменная). ; Если a <= b, то флаг заема сброшен, и 'c' будет равно 0. Если a > b, то флаг заема установлен и 'c' будет равно -1 AND c, b ; выполнить битовую операцию (c & b), записав результат в 'c'. Если a <= b, то флаг заема равен нулю, 'c' равно 0, ; значит, с =(c & b) == 0, в противном случае: c == b - a ; ADD a, c ; выполнить сложение содержимого 'a' со значением 'c', записав результат в 'a'. ; если a <= b, то c = 0 и a = a ; если a > b, то c = b - a, и a = a + (b-a) == b Компилятор msvc поддерживает замену ветвлений математическими операциями, однако использует несколько другую технику, отдавая предпочтение инструкции SETcc xxx, устанавливающую xxx в единицу, если условие сс истинно. Как показывает практика, msvc оптимизирует только ветвления константного типа, т.е. «if (n > m) a = 66; else a = 99;» еще оптимизируется, а «if (n > m) a = x; else a = y;» уже нет. Компилятор gcc, использующий инструкцию условного присвоения CMOVcc, оптимизирует все конструкции типа min, max, set flags, abs и т. д., что существенно увеличивает производительность, однако требует как минимум Pentium Pro (инструкция SETcc работает и на Intel 80386). За это отвечают ключи -fif-conversion и -fif-conversion2, которые на платформе Intel эквивалентны друг другу. (Вообще говоря, gcc поддерживает множество ключей, отвечающих за ликвидацию ветвлений, однако на платформе Intel они лишены смысла, поскольку в лексиконе x86-процессоров просто нет соответствующих команд!). Компилятор icl – единственный из всех трех, кто не заменяет ветвления математическими операциями (что в свете активной агитации за команды SBB/CMOVcc, развернутой компанией Intel, выглядит довольно странно). Во всяком случае компилятор не делает этого явно и в качестве компенсации предлагает использовать интринсики (от английского «intrinsic», буквально «внутренний»; нестандартные операторы языка, непосредственно транслирующиеся в машинный код. За более подробным описанием обращайтесь к руководству на компилятор) и функции мультимедийной библиотеки SIMD. В частности, цикл вида: Листинг 24. Неоптимизированный вариант с ветвлениями short a[4], b[4], c[4]; for (i=0; i<4; i++) c[i] = a[i] > b[i] ? a[i] : b[i]; может быть переписан так: Листинг 25. Устранение ветвлений путем использования функции select_gt библиотеки классов Intel SIMD Is16vec4 a, b, c // функция векторного поиска максимума без ветвлений c = select_gt(a, b, a, b); Естественно, такой код непереносим и на других компиляторах он работать не будет, поэтому, прежде чем подсаживаться на Intel, следует все взвесить и тщательно обдумать. Тем более что альтернативные мультимедийные библиотеки имеются и на других компиляторах. Оптимизация switch Оператор множественного выбора switch очень популярен среди программистов (особенно разработчиков Windows-приложений). В некоторых (хотя и редких) случаях, операторы множественного выбора содержат сотни (а то и тысячи) наборов значений, и если решать задачу сравнения «в лоб», время выполнения оператора switch окажется слишком большим, что не лучшим образом скажется на общей производительности программы, поэтому пренебрегать его оптимизацией ни в коем случае нельзя. Балансировка логического дерева Если отвлечься от устоявшейся идиомы «оператор switch дает специальный способ выбора одного из многих вариантов, который заключается в проверке совпадения значения данного выражения с одной из заданных констант в соответствующем ветвлении», легко показать, что switch представляет собой завуалированный оператор поиска соответствующего case-значения. Последовательный перебор всех вариантов, соответствующий тривиальному линейному поиску – занятие порочное и крайне неэффективное. Допустим, наш оператор switch выглядит так: Листинг 26. Неоптимизированный вариант оператора множественного выбора switch (a) { case 98 : /* код обработчика */ break; case 4 : /* код обработчика */ break; case 3 : /* код обработчика */ break; case 9 : /* код обработчика */ break; case 22 : /* код обработчика */ break; case 0 : /* код обработчика */ break; case 11 : /* код обработчика */ break; case 666: /* код обработчика */ break; case 96 : /* код обработчика */ break; case 777: /* код обработчика */ break; case 7 : /* код обработчика */ break; } Тогда соответствующее ему неоптимизированное логическое дерево будет достигать в высоту одиннадцати гнезд (см. рис. 1 слева). Причем на левой ветке корневого гнезда окажется аж десять других гнезд, а на правой – вообще ни одного. Чтобы исправить «перекос», разрежем одну ветку на две и прицепим образовавшиеся половинки к новому гнезду, содержащему условие, определяющее, в какой из веток следует искать сравниваемую переменную. Например, левая ветка может содержать гнезда с четными значениями, а правая – с нечетными. Но это плохой критерий: четных и нечетных значений редко бывает поровну и вновь образуется перекос. Гораздо надежнее поступить так: берем наименьшее из всех значений и бросаем его в кучу А, затем берем наибольшее из всех значений и бросаем его в кучу B. Так повторяем до тех пор, пока не рассортируем все имеющиеся значения (см. рис. 1 справа). Поскольку, оператор switch требует уникальности каждого значения, т. е. каждое число может встречаться лишь однажды, легко показать, что:
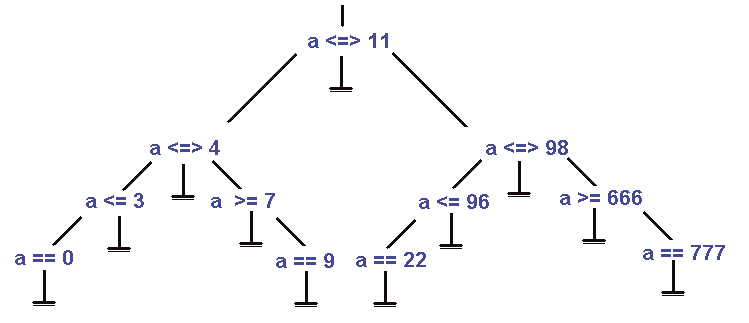
Рисунок 1. Несбалансированное (слева) и сбалансированное (справа) switch/case-дерево Высота вновь образованного дерева будет равна 1+(N+1)/2, где N – количество гнезд старого дерева. Действительно, мы же делим ветвь дерева надвое и добавляем новое гнездо – отсюда и берется N/2 и +1, а (N+1) необходимо для округления результата деления в большую сторону. То есть если высота неоптимизированного дерева достигала 100 гнезд, то теперь она уменьшилась до 51. Говорите, 51 все равно много? Но кто нам мешает разбить каждую из двух ветвей еще на две? Это уменьшит высоту дерева до 27 гнезд! Аналогично, последующее уплотнение даст 16 –> 12 –> 11 –> 9 –> 8… и все! Более плотная упаковка дерева уже невозможна. Но, согласитесь, восемь гнезд – это не сто! Оптимизированный вариант оператора switch в худшем случае потребует лишь пяти сравнений, но и это еще не предел! Учитывая, что x86 процессоры все три операции сравнения <, =, > совмещают в одной машинной команде, двоичное логическое дерево можно преобразовать в троичное, тогда новых гнезд для его балансировки добавлять не нужно. Простейший алгоритм, называемый методом отрезков, работает так: сортируем все числа по возрастанию и делим получившийся отрезок пополам. Число, находящееся посередине (в нашем случае это 11), объявляем вершиной дерева, а числа, расположенные слева от него, – его левыми ветвями и подветвями (в нашем случае это 0, 3, 4 и 7). Остальные числа (22, 96, 98, 666, 777) идут направо. Повторяем эту операцию рекурсивно до тех пор, пока длина подветвей не сократится до единицы. В конечном счете, вырастет следующее дерево: Рисунок 2. Троичное дерево, частично сбалансированное методом отрезков Очевидно, что это не самое лучшее дерево из всех. Максимальное количество сравнений (т.е. количество сравнений в худшем случае) сократилось с пяти до четырех, а количество ветвлений возросло вдвое, в результате чего, время выполнения оператора switch только возросло. К тому же структура построения дерева явно не оптимальна. Гнезда (a<=3), (a>=7), (a<=96), (a>=666) имеют свободные ветви, что увеличивает высоту дерева на единицу. Но, может быть, компилятор сумеет это оптимизировать? Дизассемблирование показывает, что компилятор msvc генерирует троичное дерево, сбалансированное по улучшенному алгоритму отрезков, содержащее всего лишь 7 операций сравнения, 9 ветвлений и таблицу переходов на 10 элементов (см. «Создание таблицы переходов»). В худшем случае выполнение оператора switch требует 3 сравнений и 3 ветвлений. Троичное дерево, построенное компилятором gcc, сбалансировано по классическому алгоритму отрезков и состоит из 11 сравнений и 24 ветвлений. В худшем случае выполнение оператора switch растягивается на 4 сравнения и 6 ветвлений. Компилятор icl, работающий по принципу простого линейного поиска, строит двоичное дерево из 11 сравнений и 11 ветвлений. В худшем случае все узлы дерева «пережевываются» целиком. Вот так «оптимизация»! Создание таблицы переходов Если значения ветвей выбора представляют собой арифметическую прогрессию (см. листинг 27), компилятор может сформировать таблицу переходов – массив, проиндексированный case-значениями и содержащий указатели на соответствующие им case-обработчики. В этом случае сколько бы оператор switch ни содержал ветвей – одну или миллион, – он выполняется за одну итерацию. Красота! Листинг 27. Неоптимизированный switch, организованный по принципу упорядоченной арифметической прогрессии switch (a) { case 1 : /* код обработчика */ break; case 2 : /* код обработчика */ break; case 3 : /* код обработчика */ break; case 4 : /* код обработчика */ break; case 5 : /* код обработчика */ break; case 6 : /* код обработчика */ break; case 7 : /* код обработчика */ break; case 8 : /* код обработчика */ break; case 9 : /* код обработчика */ break; case 10 : /* код обработчика */ break; case 11 : /* код обработчика */ break; } Листинг 28. Дизассемблерный листинг оптимизированного варианта оператора switch cmp eax, 0Bh ; switch 12 cases ; сравниваем a с 11 ja short loc_80483F5 ; default ; если a > 11 выходим из оператора switch ; jmp ds:off_804857C[eax*4] ; switch jump ; передаем управление соответствующему case-обработчику, таким образом, мы имеем всего лишь ; одно сравнение и два ветвления ; // таблица смещений case-обработчиков off_804857C dd offset loc_80483F5 ; DATA XREF: main+11r dd offset loc_80483E8 ; jump table for switch statement dd offset loc_80483F9 dd offset loc_8048402 dd offset loc_804840B dd offset loc_8048414 dd offset loc_804841D dd offset loc_8048426 dd offset loc_804842F dd offset loc_8048438 dd offset loc_8048441 dd offset loc_804844F Создавать таблицы переходов умеют все три рассматриваемых компилятора, даже если элементы прогрессии некоторым образом перемешаны: Листинг 29. Неоптимизированный switch, организованный по принципу упорядоченной арифметической прогрессии switch (a) { case 11 : /* код обработчика */ break; case 2 : /* код обработчика */ break; case 13 : /* код обработчика */ break; case 4 : /* код обработчика */ break; case 15 : /* код обработчика */ break; case 6 : /* код обработчика */ break; case 17 : /* код обработчика */ break; case 8 : /* код обработчика */ break; case 19 : /* код обработчика */ break; case 10 : /* код обработчика */ break; case 21 : /* код обработчика */ break; } Если один или несколько элементов прогрессии отсутствуют, соответствующие им значения дополняются фиктивными переходниками к default-обработчику. Таблица переходов от этого, конечно, «распухает», однако на скорости выполнения оператора switch это практически никак не отражается. Однако при достижении некоторой пороговой величины «разрежения» таблица переходов внезапно трансформируется в двоичное/троичное дерево. Компилятор msvc – единственный из всех трех, способный комбинировать таблицы переходов с логическими деревьями. Разряженные участки с далеко отстоящими друг от друга значениями монтируются в виде дерева, а густо населенные области упаковываются в таблицы переходов. Вернемся к листингу 26. Значения 9, 11, 22, 74, 666, 777 упорядочиваются в виде дерева, а 0, 3, 4, 7, 9 ложатся в таблицу переходов, благодаря чему достигается предельно высокая скорость выполнения, далеко опережающая конкурентов. Свободная таблица
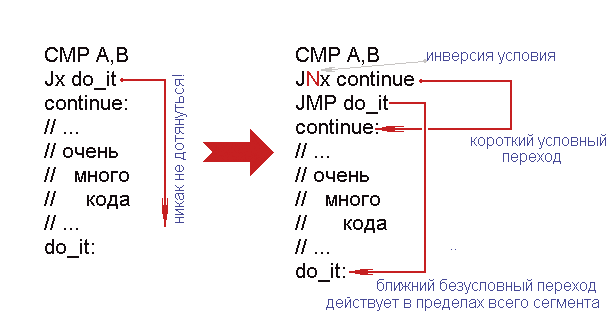
Заключение Справедливости ради оливковая ветвь пальмы первенства на этот раз не достанется никому. Все три компилятора показывают одинаково впечатляющий результат, но прокалываются в мелочах. Позиция icl выглядит достаточно сильной, однако на безусловное господство никак не тянет. Как минимум ему предстоит научиться выравнивать переходы, заменять ветвления математическими операциями и переваривать оператор switch. Компилятор gcc, с учетом его бесплатности, по-прежнему остается наилучшим выбором. Он реализует многие новомодные способы оптимизации ветвлений (в частности, использует инструкцию CMOVcc), однако по ряду позиций проигрывает насквозь коммерческому msvc, лишний раз подтверждая основной лозунг Microsoft: «Bill always win». При переходе от ветвлений к циклам (а циклы, как известно, «съедают» до 90% производительности программы), этот разрыв лишь усиливается. Но о циклах в другой раз. Это слишком объемная, хотя и увлекательная тема. Современные компиляторы не только выбрасывают из цикла все ненужное (например, заменяют цикл с предусловием на цикл с постусловием, который на одно ветвление короче), но и трансформируют сам алгоритм, подгоняя порядок обработки данных под особенности архитектуры конкретного микропроцессора. Приложение Трансляция коротких условных переходов Одна из неприятных особенностей процессоров x86 – ограниченная «дальнобойность» команд условного перехода. Разработчики микропроцессора в стремлении добиться высокой компактности кода отвели на целевой адрес всего один байт, ограничив тем самым длину прыжка интервалом в 255 байт. Это так называемый короткий (short) переход, адресуемый относительным знаковым смещением, отсчитываемым от начала следующей за инструкцией перехода командой (см. рис. 3). Такая схема адресации ограничивает длину прыжка «вперед» (т.е. «вниз») всего 128 байтами, а «назад» (т.е. «вверх») и того меньше – 127! (Прыжок вперед короче потому, что ему требуется «пересечь» и саму команду перехода). Этих ограничений лишен ближний (near) безусловный переход, адресуемый двумя байтами и действующий в пределах всего сегмента. Рисунок 3. Внутреннее представление короткого (short) перехода Короткие переходы усложняют трансляцию ветвлений – ведь не всякий целевой адрес находится в пределах 128 байт! Существует множество путей обойти это ограничение. Наиболее популярен следующий прием: если транслятор видит, что целевой адрес выходит за пределы досягаемости условного перехода, он инвертирует условие срабатывания и совершает короткий (short) переход на метку continue, а на do_it передает управление ближним (near) переходом, действующим в пределах одного сегмента. Рисунок 4. Трансляция коротких переходов Начиная с Intel 80386 в лексиконе процессора появились пятибайтные команды условных переходов, «бьющие» в пределах всего четырехгигабайтного адресного пространства, однако в силу своей относительно невысокой производительности, они так и остались невостребованными. Советы
|
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 КРИС КАСПЕРСКИ
КРИС КАСПЕРСКИ