|
Рубрика:
Наука и технологии
|
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
 АФРАЙМОВИЧ Л.Г., ННГУ им. Н. И. Лобачевского, Институт Информационных Технологий, Математики и Механики, кафедра «Информатики и автоматизации научных исследований» АФРАЙМОВИЧ Л.Г., ННГУ им. Н. И. Лобачевского, Институт Информационных Технологий, Математики и Механики, кафедра «Информатики и автоматизации научных исследований»
 ТЮНТЯЕВ А.С., ННГУ им. Н. И. Лобачевского, Институт Информационных Технологий, Математики и Механики, кафедра «Информатики и автоматизации научных исследований» ТЮНТЯЕВ А.С., ННГУ им. Н. И. Лобачевского, Институт Информационных Технологий, Математики и Механики, кафедра «Информатики и автоматизации научных исследований»
 ТЮНТЯЕВА Л.А., ННГУ им. Н. И. Лобачевского, Институт Информационных Технологий, Математики и Механики, кафедра «Информатики и автоматизации научных исследований» ТЮНТЯЕВА Л.А., ННГУ им. Н. И. Лобачевского, Институт Информационных Технологий, Математики и Механики, кафедра «Информатики и автоматизации научных исследований»
Исследование комбинированного
решения трехиндексной задачи о назначениях
Трехиндексная аксиальная задача о назначениях, подробно рассматриваемая в данной статье, является частным случаем многоиндексных задач о назначениях и имеет широкий спектр приложений, что говорит об ее актуальности. В статье изложено исследование задачи, в ходе которого: реализован алгоритм метода ветвей и границ с разными стратегиями ветвления и возможностью выбора алгоритма подсчета нижних оценок; проведен вычислительный эксперимент с решением задач разных размерностей; проведен анализ полученных результатов. Цель исследования – поиск наилучшей (с точки зрения затраченного времени) комбинации параметров алгоритма (стратегий ветвления, выбора алгоритма подсчета нижних оценок) для решения поставленной задачи
Введение
Многоиндексные задачи о назначениях (подкласс широкого класса прикладных задач, формализуемых в виде многоиндексных задач (целочисленного) линейного программирования транспортного типа) возникают:
- в теории расписаний:
- при планировании изготовления скоропортящейся продукции,
- при планировании прохождения практики студентами,
- при планировании учебы клинических ординаторов по отделениям,
- при составлении расписания занятий,
- при планировании спортивных матчей [1, 4],
- в области технического анализа данных:
- при сопровождении объектов в многосенсорных системах [1, 6],
- в военной области:
- при назначении военной техники на цели [1, 7].
Класс многоиндексных задач о назначениях, начиная с трехиндексных, является NP (non-deterministic polynomial) – трудным, то есть на данный момент не известны эффективные алгоритмы для их решения.
Трехиндексная аксиальная задача о назначениях (далее просто задача), подробно рассматриваемая в данной статье, является частным случаем многоиндексных задач о назначениях и имеет широкий спектр приложений [1-4, 8, 9], что говорит об ее актуальности.
В статье изложено исследование задачи, в ходе которого:
- реализован алгоритм метода ветвей и границ с разными стратегиями ветвления и возможностью выбора алгоритма подсчета нижних оценок;
- проведен вычислительный эксперимент с решением задач разных размерностей;
- проведен анализ полученных результатов.
Цель исследования – поиск наилучшей (с точки зрения затраченного времени) комбинации параметров алгоритма (стратегий ветвления, выбора алгоритма подсчета нижних оценок) для решения поставленной задачи.
В первом разделе представлены формальное описание и математическая модель задачи.
Второй раздел посвящен описанию алгоритмов, реализованных для решения задачи.
В третьем разделе представлены результаты вычислительного эксперимента и сделаны выводы относительно работы реализованного алгоритма.
Формальная постановка задачи
Есть исполнители, работы и орудия труда, которыми исполнители могут пользоваться при исполнении работ. Заданы зарплаты от назначения исполнителей на работы при использовании того или иного орудия труда. Надо так назначить исполнителей на работы, чтобы:
- каждый исполнитель получил не более одной работы и не более одного орудия труда;
- каждую работу делал не более, чем один исполнитель, не более, чем одним орудием труда;
- каждое орудие труда использовалось не более, чем одним исполнителем для выполнения не более, чем одной работы;
- суммарная стоимость назначений была минимальной.
Критерии и ограничения математической модели задачи представлены ниже:
 (1) (1)
 (1’) (1’)
 (2) (2)
 (3) (3)
 (4) (4)
 (5) (5)
где I=J=K={1,2,…n} – множества работников, работ и орудий труда соответственно.
Критерий задачи (1’) записан с декомпозиционной матрицей стоимостей, где:
- cijk=m1ij+m2jk+m3ik;
- C=||cijk||(n×n×n) – трехиндексная матрица зарплат порядка n;
- M1=||m1ij||(n×n×n) – матрица стоимости выполнения i-м работником j-й работы, ∀i∈I, ∀j∈J;
- M2=||m2jk||(n×n×n) – матрица стоимости выполнения j-й работы k-м орудием труда ∀j∈J, ∀k∈K;
- M3=||m3ik||(n×n×n) – матрица стоимости пользования i-го исполнителя k-м орудием труда, ∀i∈I, ∀k∈K.
Далее будет рассматриваться задача с математической моделью (1’) – (5), так как архитектура построенного алгоритма работает только для задач такого вида, задача также является NP – трудной [5].
Алгоритм решения задачи
Для решения трехиндексной аксиальной задачи о назначениях используется метод ветвей и границ. С его помощью множество допустимых решений задачи разбивается на подмножества, в которых в дальнейшем ищется оптимум исходной задачи.
Элемент разбиения представляет собой последовательное назначение ik→jk, ∀k∈K на k-м шаге ветвления. Для каждого элемента разбиения вычисляется верхняя и нижняя оценки. Также на каждом шаге элементы разбиения подвергаются процедуре отсева. Процедура отсева происходит следующим образом:
Если нижняя оценка p-го элемента разбиения (Hp,p∈{1,…n}), найденная на k-м шаге ветвления (k=(1,n)) не меньше, чем верхняя оценка s-го элемента разбиения на том же шаге ветвления (Bs,p∈{1,…n}), то ветка (подмножество решений исходной задачи), содержащая s-й элемент разбиения, отсекается (исключается из дальнейшего рассмотрения для поиска решения).
Формальное описание условия процедуры отсева:
Hp≥Bs, p,s=(1,n)
Глобальный оптимум задачи ищется на листьях, у которых известны все назначения i→j симплекс-методом. Каждый такой лист содержит n! допустимых решений, оптимум среди которых можно найти за полиномиальное время за счет сведения задачи к двухиндексной задаче о назначениях.
Специфика данной архитектуры ветвления состоит в том, что она работает только для задач с декомпозиционными стоимостями.
Описание стратегий ветвления, использованных в алгоритме метода ветвей и границ:
- Ветвление в глубину (Length) – при использовании данной стратегии на k-м шаге ветвления выбирается такой элемент разбиения, количество назначений ik→jk которого наибольшее (k=(1,n));
- Ветвление в ширину (Width) – при использовании данной стратегии на k-м шаге ветвления выбирается такой элемент разбиения, количество назначений ik→jk которого наименьшее (k=(1,n));
- Ветвление по минимальной верхней оценке (EffectiveHB) – при использовании данной стратегии на k-м шаге ветвления выбирается такой элемент разбиения s, верхняя оценка которого наименьшая по сравнению с верхними оценками элементов разбиения, полученных до k-го шага включительно (Вs=minВk, где Вk – множество верхних оценок элементов разбиения, известных на k-м шаге алгоритма (k=(1,n));
- Ветвление по минимальной нижней оценке (LowMax-Branch) – при использовании данной стратегии на k-м шаге ветвления выбирается такой элемент разбиения s, нижняя оценка которого наименьшая по сравнению с нижними оценками элементов разбиения, полученных до k-го шага включительно (Hs=minHk, где Hk – множество нижних оценок элементов разбиения, известных на k-м шаге алгоритма (k=(1,n));
- Ветвление по гибридной оценке (Gybrid) – при использовании данной стратегии на k-м шаге ветвления выбирается такой элемент разбиения s, отношение нижней оценки которого к верхней не менее 0,9 (Hs/Bs≥0,9). При этом на нижнюю оценку выбранного s-го элемента разбиения накладывается дополнительное условие: она должна отличаться от минимальной нижней оценки из множества, (Hk – множество нижних оценок элементов разбиения, известных на k-м шаге алгоритма (k=(1,n)) не более, чем на 10%. (Нижние оценки, удовлетворяющие данному условию, будем называть «хорошими»). Если нет элемента разбиения, удовлетворяющего данным условиям, то берется элемент с наименьшим количеством назначений ik→jk (k=(1,n));
- Ветвление по разностной оценке (Substraction) – при использовании данной стратегии на k-м шаге ветвления выбирается такой элемент разбиения s, разность между верхней и нижней оценкой которого минимальна (Bs–Hs→min);
- Ветвление по соотношению оценок (Ratio) – при использовании данной стратегии на k-м шаге ветвления выбирается такой элемент разбиения s, отношение нижней оценки которого к верхней максимально. (Hs/Bs→max). При этом на нижнюю и верхнюю оценки выбранного s-го элемента разбиения накладываются следующие дополнительные условия: они должны соответственно отличаться от минимальной нижней и верхней оценки из множеств Hk, Bk (где Hk, Bk – множество нижних и верхних оценок элементов разбиения, известных на k-м шаге алгоритма (k=(1,n)) не более, чем на 30%. Если нет элемента разбиения, удовлетворяющего всем данным условиям, то берется элемент с наименьшим количеством назначений ik→jk (k=(1,n)).
При подсчете верхней оценки листа используется жадный алгоритм (для каждого элемента ∀i∈I выбираются допустимые элементы ∀j∈J и ∀k∈K, при которых стоимость назначения минимальна).
Подсчитать нижнюю оценку листа, при реализации используемого алгоритма, можно двумя способами:
- Симплекс метод. Идея метода – избавиться от целочисленности и изменить (5) ограничение задачи на ограничение вида:
 (6) (6)
- Потоковый алгоритм (алгоритм поиска потока минимальной стоимости с двусторонними пропускными способностями). Данный алгоритм находит оптимальное решение трех двухиндексных задач о назначениях, которые получаются при декомпозиции исходной трехиндексной матрицы с учетом уже известных (полученных ранее) назначений i→j элемента разбиения. Оптимально назначаются исполнители на работы, оптимально выбираются орудия труда для работ и оптимально выбираются орудия труда для исполнителей. Далее, подсчитывается общая суммарная стоимость от решения всех трех двухиндексных задач, которая и представляет собой нижнюю оценку для вершины.
Вычислительный эксперимент
Для решения задач данного класса описанным алгоритмом было написано программное приложение в интегрированной среде разработки Visual Studio Professional 2017 (Windows Forms, язык программирования C#).
Вычисления проводились на вычислительной технике фирмы ASUS. Процессор: Intel® Core ™ i5 – 3230M CPU @ 2.60GHz. Тип системы: 64 – разрядная операционная система, процессор х64, операционная система: Windows 8.
На рис. 1 представлено диалоговое окно приложения, в котором выбираются параметры для решения задач. В реализации алгоритма предусмотрены выбор параллельного или последовательного подсчета верхних и нижних оценок для «потомков» вершины, а также последовательный или же параллельный запуск стратегий ветвления. Приложение позволяет генерировать задачи случайным образом или решать предложенные задачи.
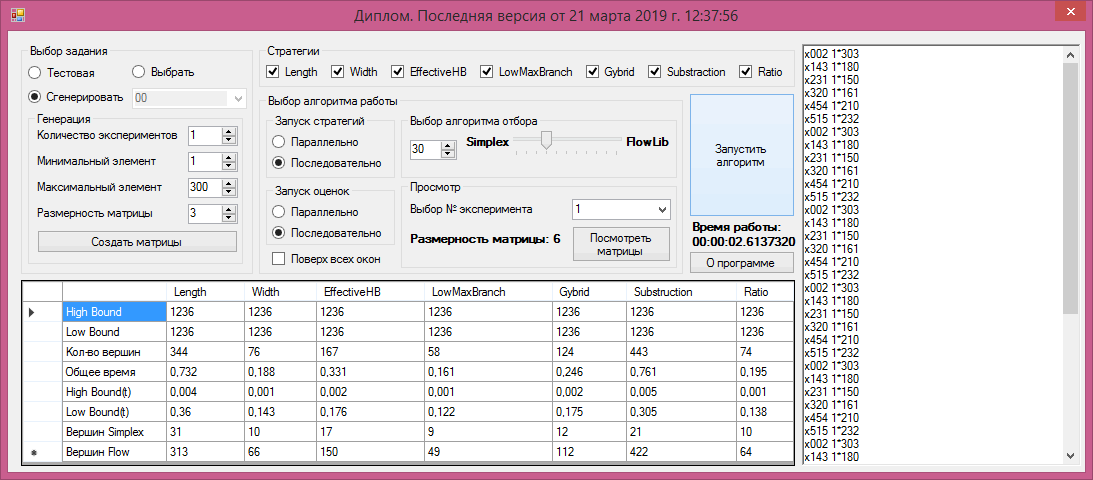
Рисунок 1. Диалоговое окно приложения, в котором выбираются параметры для решения задач
В ходе вычислительного эксперимента тестировались задачи размерностей (n) равных:
- 6 (2 задачи),
- 10 (2 задачи),
- 15 (2 задачи),
- 33 (задача с известным оптимумом и решением [10]).
Цели вычислительного эксперимента:
- путем вычисления задач с известными оптимальными решениями убедиться, что реализованный алгоритм работает верно;
- найти наилучшую, с точки зрения затраченного времени, комбинацию параметров алгоритма (стратегии ветвления, выбор алгоритма подсчета нижних оценок) для решения этого класса задач.
Стратегия подсчета нижней оценки для каждого листа выбиралась таким образом:
если у вершины «родителя» соотношение
 (7) (7)
(x=0%; 5%; 10%; 20%; 30%; 50%; 100%), то у всех «наследников вершины» нижняя оценка считается потоковым алгоритмом, иначе – симплекс методом.
Нижняя оценка начальной вершины всегда считается симплекс методом. Ниже представлен фрагмент таблицы с результатами вычислительного эксперимента.
Время работы алгоритма в зависимости от выбора параметров
В первом столбце таблицы 1 приведены размерности тестируемых задач. В следующих столбцах приведено время (мин_мин:сек_сек,мсек) работы алгоритма в зависимости от выбранных параметров, где первая строка – процент, меньше которого должно быть соотношение (8), чтобы нижняя оценка вершины «потомка» считалась потоковым алгоритмом.
Таблица 1.
| n |
0% |
5% |
10% |
20% |
30% |
50% |
100% |
| 6 |
00:00,948 |
00:00,868 |
00:00,984 |
00:01,947 |
00:02,614 |
00:04,880 |
00:06,565 |
| 6 |
00:03,271 |
00:03,228 |
00:03,352 |
00:03,582 |
00:05,719 |
00:11,840 |
00:13,252 |
| 10 |
01:18,890 |
01:15,256 |
01:24,010 |
01:59,669 |
12:15,877 |
>20 мин |
>20 мин |
| 10 |
00:44,207 |
00:43,532 |
00:48,158 |
01:13,416 |
05:43,865 |
>20 мин |
>20 мин |
| 15 |
04:26,672 |
04:31,905 |
04:37,223 |
>20 мин |
>20 мин |
>20 мин |
>20 мин |
| 15 |
04:46,914 |
04:51,590 |
04:59,800 |
09:01,099 |
>20 мин |
>20 мин |
>20 мин |
Задачи размерности, начиная с n=15 при параллельном запуске подсчета оценок, считаются дольше 30 мин, поэтому задачи размерностей выше 15 будем считать второй по эффективности (выявлено из предыдущих экспериментов) стратегией ветвления EffectiveHB, так как при решении самой эффективной стратегией LowMaxBranch при выборе процентов для соотношения (7) в диапазоне 5% – 30% разница времен выполнения задачи несущественна.
На рис. 2 представлено решение задачи размерностью 33 с известным оптимумом. Решение, полученное нашим алгоритмом, совпадает с известным оптимумом, что говорит о том, что реализованный алгоритм работает верно, ошибок в реализации нет.
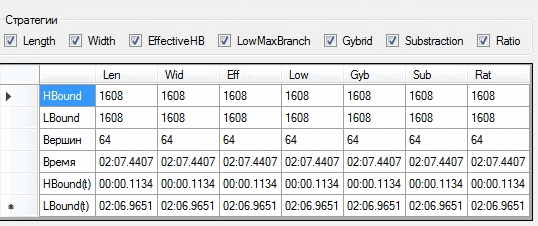
Рисунок 2. Решение задачи размерностью 33 с известным оптимумом
Заключение
В ходе исследования и вычислительного эксперимента было установлено:
- при решении задач с известными оптимальными решениями [10] вышеизложенным алгоритмом, решения совпали с известными решениями;
- выявлено, что при выполнении соотношения (8) в диапазоне 5% – 10%, тестировавшиеся задачи считаются наименьшее время. Однако при решении задач больших размерностей данный алгоритм не всегда находит решение за приемлемое время. Следовательно, чтобы сократить время решения задач больших размерностей, планируется усовершенствование данного алгоритма, например, реализация других алгоритмов подсчета верхней, нижней оценок, более детальное распараллеливание алгоритма и т.д.
- He Jiang, Shuwei Zhang, Zhilei Ren, Xiaochen Lai, and Yong Piao «Approximate Muscle Guided Beam Search for Three-Index Assignment Problem» Software School, Dalian University of Technology, Dalian,116621,China jiangle@dlut.edu.cn
- A. M. C. Ficker, L. G. Afraimovich, F. C. R. Spieksma The axial 3-Dimensional Problem with perimeter costs revisited. Proceedings of the 12th Workshop on Models and Algorithms for Planning and Scheduling Problems. MAPSP 2015. La Roche-en-Ardenne, Belgium. 8-12 June 2015. P. 83-85.
- Афраймович Л. Г. «Эвристические методы решения целочисленных декомпозиционных многоиндексных задач», Автоматика и телемеханика, 2014. № 8. С. 3–18.
- Афраймович Л. Г. «Многоиндексные транспортные задачи с 2-вложенной структурой», Автоматика и телемеханика, 2013. № 1. С. 116-134.
- Burkard R.E., Rudolf R., Woeginger G.J. Three-dimensional axial assignment problems with decomposable cost coefficients // Discrete Applied Mathematics. 1996. V. 65. P. 123–139
- Pusztaszeri J.F., Rensing P.E., Liebling T.M. Tracking elementary particles near their primary vertex: A combinatorial approach // Journal of Global Optimization. 1996. V. 9. P. 41–64.
- Alighanbari M., How J.P. Cooperative task assignment of unmanned aerial vehicles in adversarial environments // Proceedings of the American Control Conference. 2005. V. 7. P. 4661–4666.
- Афраймович Л.Г., Прилуцкий М.Х. Многоиндексные задачи оптимального планирования производства // Автоматика и телемеханика. 2010. № 10. C. 148-155.
- Афраймович Л.Г. Многоиндексные транспортные задачи с декомпозиционной структурой // Автоматика и телемеханика. 2012. № 1. С. 130-147.
- http://www.win.tue.nl/~fspieksma/instancesEJOR.htm
Ключевые слова: трехиндексная задача о назначениях, алгоритм метода ветвей и границ.
Investigation of the combined solution of the three-index assignment problem
Afraimovich L.G., Tyuntyaev A.S., Tyuntyaeva L.A., UNN them. N.I. Lobachevsky, Institute of Information Technologies, Mathematics and Mechanics, Department of "Informatics and automation of scientific research"
Abstract: The three-index axial assignment problem, which is discussed in detail in this article, is a special case of multi-index assignment problems and has a wide range of applications, which indicates its relevance. The article presents a study of the problem, during which: the algorithm of the branch and bound method is implemented with different branching strategies and the possibility of choosing an algorithm for counting lower bounds; a computational experiment was conducted with solving problems of different dimensions; The analysis of the obtained results. The purpose of the study is to find the best (in terms of elapsed time) combination of algorithm parameters (branching strategies, selection of a lower bound calculation algorithm) to solve the problem.
Keywords: three-index assignment problem, branch and bound algorithm.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|











 АФРАЙМОВИЧ Л.Г., ННГУ им. Н. И. Лобачевского, Институт Информационных Технологий, Математики и Механики, кафедра «Информатики и автоматизации научных исследований»
АФРАЙМОВИЧ Л.Г., ННГУ им. Н. И. Лобачевского, Институт Информационных Технологий, Математики и Механики, кафедра «Информатики и автоматизации научных исследований» ТЮНТЯЕВА Л.А., ННГУ им. Н. И. Лобачевского, Институт Информационных Технологий, Математики и Механики, кафедра «Информатики и автоматизации научных исследований»
ТЮНТЯЕВА Л.А., ННГУ им. Н. И. Лобачевского, Институт Информационных Технологий, Математики и Механики, кафедра «Информатики и автоматизации научных исследований»




