|
Рубрика:
Наука и технологии
|
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
 ПОВАЛЯЕВ П.П., Московский авиационный институт (национально исследовательский университет), инженер ПОВАЛЯЕВ П.П., Московский авиационный институт (национально исследовательский университет), инженер
 КАЛЁНОВА Н.В., Московский авиационный институт (национально исследовательский университет), доцент КАЛЁНОВА Н.В., Московский авиационный институт (национально исследовательский университет), доцент
 РОМАНЕНКОВ А.М., Московский авиационный институт (национально исследовательский университет), доцент РОМАНЕНКОВ А.М., Московский авиационный институт (национально исследовательский университет), доцент
 ШАРИКОВ Д.В., Московский авиационный институт (национально исследовательский университет), инженер ШАРИКОВ Д.В., Московский авиационный институт (национально исследовательский университет), инженер
Движения ступеней ракет-носителей
для уменьшения зон «отчуждения»
В данной работе, рассмотрен подход, который позволит исследовать движение ступеней ракет-носителей. Для примера был рассмотрен запуск ракеты-носителя «Союз», а точнее критическое падение второй ступени. Чтобы выработать рекомендации для уменьшения зоны «отчуждения», реализована методика численного моделирования свободных колебаний модели. Была доработана базовая программа, основанная на методе Годунова – Родионова интегрирования нестационарных уравнений Эйлера, путем дополнения блоком интегрирования обыкновенного дифференциального уравнения плоского движения тела (включающий в себя плоское угловое движение и движение центра масс) с учетом изменений параметров набегающего потока за счет изменения высоты. Для решения газодинамической задачи, разработана программа построения трехмерной структурированной вычислительной сетки, в прямоугольной системе координат. Обработаны полученные данные и визуализированы в специализированных программных пакетах такие как Tecplot и Grapher 2.0
При запуске ракеты-носителя образуются зоны падения отработанных ступеней и их обломков в различных районах площадью в сотни квадратных километров. Это приводит к тому, что возникают зоны «отчуждения», в которых невозможна хозяйственная деятельность и размещение населенных пунктов.
Рассмотрим запуск ракеты-носителя «Союз».
- Первая ступень совершает отделение в непосредственной близости к месту старта ракеты-носителя, где отсутствуют населенные территории.
- Вторая ступень, при падении с огромной скоростью разрушается в плотных слоях атмосферы, и обломками разносится на большие территории, тем самым создавая зону «отчуждения».
Задача данной работы – рассмотреть подход, который позволит исследовать движение ступеней ракет-носителей с целью выработок рекомендаций для уменьшения зоны «отчуждения».
Известны способы расчетов динамики падения ступеней ракет-носителей, в ходе которых заранее формировались массивы аэродинамических коэффициентов ступеней, в зависимости от числа Маха, высоты, углов атаки и набегающего потока. Далее с использованием интерполированных данных этих массивов решалась задача динамики.
Нужно реализовать методику комплексного расчета, решить одновременно уравнение газовой динамики и уравнение движения центра масс, а также и углового движения относительно центра масс.
Для интегрирования уравнения движения будет использован простейший метод Эйлера. Поскольку идет разработка методики, для ускорения времени счета используется простейший метод Эйлера, который позволяет интегрировать уравнение динамики, используя неравномерный шаг по времени.
В данной работе предлагается новая методика, в которой будет использоваться упрощенный расчет в рамках плоского гравитационного поля и производиться изменение параметров атмосферы на разной высоте. При этом не будет использоваться сложная динамика движения тела в центральном поле земли.
Исследование движения газообразной среды, т.е. определение в каждой точке пространства параметров, характеризующих это движение, состоит в решении соответствующих уравнений, которые связывают между собой эти параметры. Все эти уравнения независимы и составляют систему уравнений газодинамики. Число независимых уравнений системы определяем количеством отыскиваемых независимых параметров газа.
Рассмотрим движения идеального газа. Если скорости потока невелики, то можно пренебречь изменением удельных теплоемкостей от температуры и не учитывать излучения. В этом случае газовое течение представляет собой термодинамическую изолированную систему и является адиабатическим. Система уравнений газодинамики должна включать шесть независимых уравнений.

Запишем систему уравнений по осям прямоугольной системы координат X, Y, Z, и проекции вектора скорости u, v, w на данные оси.
Система уравнений Эйлера, записанная в дивергентной форме, имеет вид:
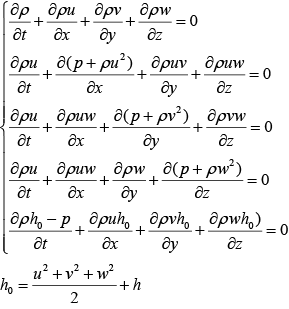 (1) (1)
В ряде случаев для определения характера движения системы требуется знать закон движения ее центра масс. Чтобы найти этот закон просуммируем левую и правую часть системы дифференциальных уравнений движения, система состоит из n материальных точек, точка системы с массой m, равнодействующая всех приложенных к точке внешних сил  , и равнодействующая всех внутренних сил , и равнодействующая всех внутренних сил  ,точка имеет ускорение an. ,точка имеет ускорение an.
 (2) (2)
Суммируя получаем
 (2) (2)
Преобразуем левую часть равенства. Из формулы (2) для радиуса-вектора центра масс получаем
 (3) (3)
Беря от обеих частей этого равенства вторую производную по времени и замечая, что производная от суммы равна сумме производных, найдем
 (4) (4)
Так как по свойству внутренних сил системы  , получим окончательно из равенства (2) учитывая (4) , получим окончательно из равенства (2) учитывая (4)
 (5) (5)
Уравнение (5) и выражает теорему о движении центра масс системы. Проектируя обе части равенства на координатные оси, получим
 (6) (6)
Эти уравнения представляют собой дифференциальные уравнения движения центра масс в проекции на оси декартовой системы координат.
Одним из наиболее эффективных методов численного решения уравнений газодинамики является метод С.К. Годунова. Годунов С.К. в 1957 году предложил численный метод решения уравнения газовой динамики, который основывается на использовании точного или приближенного решения задачи Римана.
Рассмотрим равномерную пространственную сетку с шагом ∆х. Значения сеточной функции будем обозначать, как Uki и Uki±1/2. Нижний целый индекс i=1,2,… обозначает значения функции, отнесенные к центру масс i-й дискретной ячейке. Полуцелые нижние индексы i±1/2 обозначают значения сеточной функции на границе между ячейками с номерами i и i±1. Верхний целый индекс k=0,1,2,... обозначает номер слоя (шага) по времени.
Положим, что все сеточные функции являются постоянными внутри каждой из дискретных ячеек. Тогда на границе с номером i±1/2 на каждом шаге по времени будем решать задачу Римана со следующими начальными данными:
Uki=const при x<xi+1/2 и Uki+1=const при x>xi+1/2.
Пусть Uki+1/2 – это решение такой задачи в точке x=xi+1/2. Аналогично, Uki–1/2 – это решение такой задачи в точке x=xi–1/2. Тогда явная конечно-объемная схема Годунова имеет вид:
 (7). (7).
Эта схема обладает первым порядком точности по времени и по пространству.
Схему (7) можно обобщить на неравномерные пространственные и подвижные сетки. Она также может применяться в расчетах с выделением разрывов. Рассмотрим, например, двумерную гиперболическую систему уравнений:
 (8) (8)
Конечно-объемная схема для этой системы на равномерной декартовой сетке записывается в виде:
 (9) (9)
 (10) (10)
Таким образом, для построения схемы следует решать задачу Римана на каждой из границ дискретных ячеек.
Схему Годунова (9) можно обобщить на произвольную пространственную сетку. Перепишем систему (10) в интегральной форме:
 (11) (11)
Построим явную конечно-объемную схему Годунова для уравнений в интегральной форме (13). Покроем для этого вычислительную область дискретной сеткой, состоящей из произвольных выпуклых конечных многоугольников с площадями Gi, где i=1,2,…, и с числом сторон m=m(i), каждая из которых имеет длину Sj и внешнюю нормаль nj, где j=1,2,…,m(i). Аппроксимируем интегральные уравнения на каждом из многоугольников следующим образом:
 (12) (12)
Явная конечно-объемная схема Годунова на произвольной движущейся сетке записывается в виде:
 (13) (13)
 (14) (14)
Уравнение (16) является уравнением изменения объема дискретной ячейки Gi. Оно играет роль дискретного условия совместности аппроксимаций для G и S. При заданной аппроксимации площадей S уравнение (16) можно использовать для определения объемов Gi(k+1). В ряде случаев это дает поправку к величине объема, вычисленного исходя только из геометрических соображений.
Выполнения уравнения (16) можно также добиться выбором подходящих величин Dj. Важнейшее свойство аппроксимаций G и S, которые удовлетворят соотношению (16), заключается в следующем. Решение системы уравнений (8) в виде состояния U=U0=const является также решением дискретных уравнений (15) и (16). Соблюдения этого условия следует добиваться при использовании движущихся и криволинейных систем координат.
Схема (14) устойчива на равномерной прямоугольной сетке при условии:
 (15) (15)
где Cx и Cy являются числами Куранта, соответственно, для осей х и у и определяются ∂F/∂U и ∂E/∂U. Аналогично строится, конечно-объемный метод Годунова для многомерного случая.
Рассмотрим метод Эйлера рассмотрим на примере простейшего дифференциального уравнения y'=f(x,y) с начальным условием y(x0)=y0. Подставив x0, y0, в уравнение, получим значение производной в точке x0:

При малом ∆x0 имеет место:

Обозначим f(x0,y0)=f0, перепишем последнее равенство в виде:
y1=y0+f0∙∆x
Принимая x1, y1 теперь за новую исходную точку, точно также получим:
y2=y1+f1∙∆x
В общем случае будем иметь:
y(i+1)=yi+fi∙∆x
Рассмотрим пример задачи.
Ступень со скоростью уходит вниз с высоты 80 км по вектору скорости. На нее действует сила тяжести, которая направлена по оси Y. Так же действует сила сопротивления, в результате первоначально имеем вектор скорости, который будет меняться за счет модуля скорости и направления.
Предполагается, что с высоты 80 км начинается интенсивное воздействие атмосферы на ступень ракеты-носителя со скорость ϑ0 и углом атаки α. Дальше движущая система координат двигается со скорость ϑ0 равномерно.
 (16) (16)
Строим местную систему координат, фиксируем под каким углом θ по оси Ох она войдет в атмосферу. Связываем первый момент времени с центром масс и строим систему координат x, y, так что вектор скорости ϑ направлен по оси Ох. Интегрируем систему уравнений в движущейся системе координат.
 (17) (17)
Система координат центра масс
 (18) (18)
Положение в земной системе координат
 (19) (19)
Высота будет равна  , по которой определяем параметры атмосферы на данной высоте. , по которой определяем параметры атмосферы на данной высоте.
Для интегрирования уравнения движения используем простейший метод Эйлера. При этом выполняется шаг интегрирования уравнения газовой динамики, а затем на этом же временном шаге производится расчет движения ступени. Определяется пространственное и угловое движение.
Расчетная область представляет собой сферу, в центре располагается исследуемое тело. Сфера выбрала с точки зрения, чтобы шел нормальный расчет, и формировалась поверхность ударной волны. Вокруг ступени выделяем вторую подобласть, которая со сферой образует единую область. Такая расчетная область позволит считать возле поверхности тела более точные данные, так как сетка более мелкая, и сгущена к поверхности ступени ракеты-носителя.
Для численной реализации программы используется модификация метода С.К. Годунова, предложенная в работах. Для сокращения выкладок его описание приводится на примере расчета двумерных течений. Обобщение метода на трехмерный случай, очевидно.
Численное решение системы
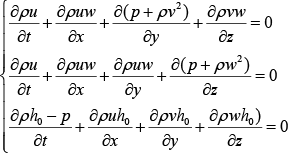 (20) (20)
осуществляется методом установления, при последовательном переходе от одного слоя t=const к другому.
Предположим, что задан алгоритм построения регулярной четырехугольной конечно-разностной сетки на каждом слое t=tl (l=1,2,3,…). Обозначим координаты узлов разностной сетки через  (j=1,...,J1; k=1,...,K1), а осредненные по элементарным плоским ячейкам параметры через ωlj–1/2,k–1/2 (ω=u,v,w,ρ,P,γ,h0). Проинтегрируем систему дифференциальных уравнений (31) по одной из элементарных ячеек от слоя х=xl до х=хl+1. В качестве примера выпишем конечно-разностный аналог уравнения: (j=1,...,J1; k=1,...,K1), а осредненные по элементарным плоским ячейкам параметры через ωlj–1/2,k–1/2 (ω=u,v,w,ρ,P,γ,h0). Проинтегрируем систему дифференциальных уравнений (31) по одной из элементарных ячеек от слоя х=xl до х=хl+1. В качестве примера выпишем конечно-разностный аналог уравнения:
 (21) (21)
Здесь ∆S – площадь элементарной ячейки в плоскости t=const, ∆t=tl+1–tl∙∏ – поток энтальпии через боковую грань ячейки, определяемый соотношением:

Где  и и  – осредненные параметры на боковых гранях ячейки: – осредненные параметры на боковых гранях ячейки:

 – площадь проекции четырехугольника с вершинами – площадь проекции четырехугольника с вершинами  на плоскость х=const. на плоскость х=const.
 – площадь проекции четырехугольника с вершинами – площадь проекции четырехугольника с вершинами  на плоскость х=const. на плоскость х=const.
Предположим, что известны осредненные параметры на l-ом слое и на четырех боковых гранях ячейки  , ,  , ,  и и  . Тогда разностные уравнения переписываются относительно неизвестных параметров . Тогда разностные уравнения переписываются относительно неизвестных параметров  : :

Уравнения сразу позволяют определить величины:

Для совершенного газа оставшиеся величины определяются по соотношениям:

Таким образом, определена процедура расчета параметров  : по известным параметрам на l-том слое и на четырех боковых гранях ячейки – : по известным параметрам на l-том слое и на четырех боковых гранях ячейки –  , ,  , ,  и и  . .
Прежде, чем перейти к описанию полной процедуры перехода от слоя t=tl к слою t=tl+1, сформулируем одно из основных предположений.
Будем полагать, что на каждом l-оме распределение параметров ω является кусочно-линейным с разрывами на линиях конечно-разностной сетки.
Для задания кусочно-линейного распределения кроме параметров, приписываемых центрам ячеек ωlj–1/2,k–1/2, будем использовать их приращения по двум направлениям:

Итак, полная процедура расчета параметров  по известным ωlj–1/2,k–1/2 ( переход от l-го слоя к l+1-му) состоит из следующих этапов. по известным ωlj–1/2,k–1/2 ( переход от l-го слоя к l+1-му) состоит из следующих этапов.
Этап I. Для каждой ячейки определяются приращения параметров [∆jῶ]lj–1/2,k–1/2 и [∆kῶ]lj–1/2,k–1/2 по известным параметрам в центрах четырех соседних ячеек и их координатам. Затем эти приращения корректируются для обеспечения монотонности кусочно-линейного распределения параметров:
[∆jῶ]lj–1/2,k–1/2=minmod{[∆jῶ]lj–1/2,k–1/2,2(ωlj+1/2,k–1/2–ωlj–1/2,k–1/2)–[∆jῶ]lj+1/2,k–1/2,2(ωlj–1/2,k–1/2–ωlj–3/2,k–1/2)–[∆jῶ]lj+1/2,k+3/2}
[∆kῶ]lj–1/2,k–1/2=minmod{[∆kῶ]lj–1/2,k–1/2,2(ωlj–1/2,k+1/2–ωlj–1/2,k–1/2)–[∆kῶ]lj–1/2,k+1/2,2(ωlj–1/2,k–1/2–ωlj–1/2,k–3/2)–[∆kῶ]lj+1/2,k+3/2}
Здесь функция minmod определяется следующим образом:

Этап II.(Шаг предиктор). Предварительно рассчитываются параметры  по описанной выше процедуре, в которой: по описанной выше процедуре, в которой:
 заменяется на заменяется на  , , заменяется на ωlj–1/2,k–1/2+([∆jω]lj–1/2,k–1/2)/2, заменяется на ωlj–1/2,k–1/2+([∆jω]lj–1/2,k–1/2)/2, заменяется на ωlj–1/2,k–1/2–([∆jω]lj–1/2,k–1/2)/2, заменяется на ωlj–1/2,k–1/2–([∆jω]lj–1/2,k–1/2)/2, заменяется на ωlj–1/2,k–1/2+([∆kω]lj–1/2,k–1/2)/2, заменяется на ωlj–1/2,k–1/2+([∆kω]lj–1/2,k–1/2)/2, заменяется на ωlj–1/2,k–1/2–([∆kω]lj–1/2,k–1/2)/2. заменяется на ωlj–1/2,k–1/2–([∆kω]lj–1/2,k–1/2)/2.
Этап III. Определяются параметры на боковых гранях ячеек из решения задачи Римана (распад разрыва) с начальными параметрами

для определения  и и

для определения  . .
Этап IV (Шаг корректор). Окончательный расчет  . .
Описанная разностная схема имеет второй порядок аппроксимации в областях в равномерной конечно-разностной сеткой и первый порядок – в местах сильной неравномерности сетки. Она обладает свойством монотонности при выполнении условий

где  – локально максимально допустимый расчетный шаг по условию Куранта-Фридрихса-Леви. – локально максимально допустимый расчетный шаг по условию Куранта-Фридрихса-Леви.
Для ускорения сходимости к стационарному решению можно использовать локальный шаг интегрирования  для каждой ячейки. В этом случае все уравнения и алгоритм расчета сохраняются за исключением задачи Римана. На подвижной разностной сетке из задачи Римана на каждой боковой грани необходимо выбирать два решения, соответствующие двум скоростям движения боковой грани. для каждой ячейки. В этом случае все уравнения и алгоритм расчета сохраняются за исключением задачи Римана. На подвижной разностной сетке из задачи Римана на каждой боковой грани необходимо выбирать два решения, соответствующие двум скоростям движения боковой грани.
Начальные условия определяются значениями параметров газа для некоторого момента времени и имеют смысл, очевидно, для неустановившегося движения. M∞=10, α=30°.
Граничное условие определяется характером течения газа на обтекаемой поверхности. Если газ невязкий и не проникает сквозь такую поверхность, то течение характеризуется условием безотрывного обтекания.
В соответствии с этим условием в каждой точке поверхности составляющая скорости, нормальная к ней, равна нулю, а вектор полно скорости совпадает с направлением касательной к поверхности.
При неустановившемся движении газа для некоторого момента t должны быть заданы значения всех искомых параметров движения vx, vy, vz, ρ, р, Т. Если движение газа установившееся, то начальные условия отпадают.
Граничные условия идеального газа. Если течение ограничено неподвижной границей, сквозь которую газ не проникает, то условием безотрывного обтекания границы газом будет равенство нулю нормальной составляющей скорости газа к поверхности границы. Если F(x,y,z)=0 – уравнение поверхности границы, то это условие запишется так:
 (23) (23)
Если же граница является подвижной поверхностью F(x,y,z,t)=0 и течение газа безотрывное, то нормальная составляющая скорости частицы в любой точке поверхности должна равняться нормальной скорости D точки самой поверхности. (20), выражается формулой:
 (24) (24)
нормальная составляющая скорости к стенке
 (25) (25)
Из равенства этих величин (поскольку G≠0) получаем:
 (26) (26)
Вычислительная сетка внутри расчетной области строится с помощью простого алгебраического генератора.
Программа для интегрирования систем уравнения, а также построение вычислительной сетки была написана на языке FORTRAN. Рассмотрим блок-схему программы (см. рис. 1).
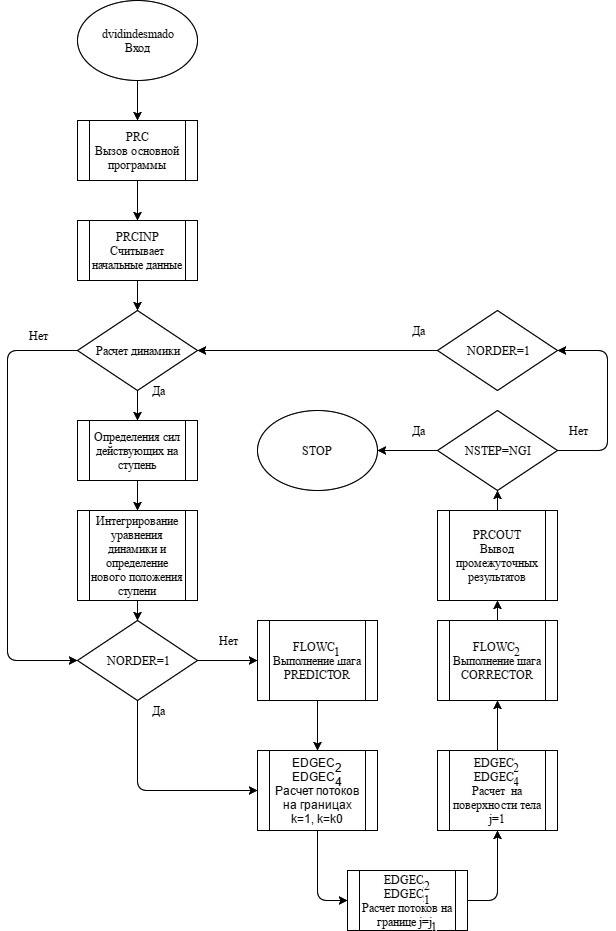
Рисунок 1. Блок-схема программы расчета
В блок схеме используется названия используемых подпрограмм и различные переменные, ниже рассмотрим подробнее, за что отвечает каждый блок в расчете. Приведем расшифровку данных из документа в таблице ниже (см. таблицу 1).
Таблица 1.
| № |
Обозначение в файле |
Идентификатор |
Описание |
| 1 |
Ipr |
Ipr |
A sign of the continuation of the calculation, 0 – the beginning of a new calculation, 1 – the continuation of the calculation |
| 2 |
Nlf |
Nlf |
Name of large M1 file |
| 3 |
Nsf |
Nsf |
Small file name M2 |
| 4 |
Cappa |
Cappa |
The shock adiabatic exponent |
| 5 |
Me |
Me |
Mach number |
| 6 |
Alf |
Alf |
Angle of attack in degrees |
| 7 |
Hf |
Hf |
Flight altitude in km |
| 8 |
J0 |
J0 |
The number of calculated intervals in the direction from the inner boundary to the outer |
| 9 |
K0 |
K0 |
Number of calculated intervals along the transverse direction |
| 10 |
I0 |
I0 |
Number of calculated intervals along the longitudinal axis of the body |
| 11 |
Sgl |
Sgl |
Shock Surface Smoothing Coefficient |
| 12 |
NST1 |
NST1 |
The number of integration steps performed with the first order of approximation |
| 13 |
NST2 |
NST2 |
The number of integration steps performed with the value of Courant number 0.4 |
| 14 |
NST3 |
NST3 |
The total number of steps of integration |
| 15 |
NST4 |
NST4 |
Interval of recording intermediate results |
| 16 |
NST5 |
NST5 |
The number of steps that determines the interval for recalculating the thermodynamic characteristics of air |
| 17 |
Rm |
Rm |
The typical size for calculating the area of the midsection |
| 18 |
NKOL |
NKOL |
Step number of the record |
Далее следуя по смоделированной блок-схеме, идет вызов подпрограммы PRC. PRC является основной подпрограммой в расчетном модуле, а для ввода данных и запись результатов используются такие подпрограммы, как PRCINP и PRCOUT.
Все три подпрограммы отвечают за ввод исходных данных и их преобразование к требуемому виду, построение конечно-разностной сетки, задание граничных условий и последовательное обращение к программам пошагового интегрирования уравнений газовой динамики, обработку и вывод результатов расчета. Решаемая задача – трехмерное обтекание осесимметричного тела совершенным газом.
PRС является основной в модуле.
SUBROUTINE PRC(DT,S1,S2,DSJ,DSK,DSI,R1,R2,FJD,FJU,FKD,FKU, FID,FIU,L0,J0,K0,I0,J1,K1,I1)
PRСINP определяет начальные данные.
SUBROUTINE PRCINP(NSTEP,DT,R,S,S0,L0,J0,K0,I0,J1,K1,I1)
PRСOUT выводит результаты расчета.
SUBROUTINE PRCOUT(NSTEP,S0,DT,R,S,L0,J0,K0,I0,J1,K1,I1,SBODY,EPS)
Файлы входных данных имеют фиксированную структуру, т.е. не допускается перестановка строчек и переменных в файле. Границы задания параметров ограничены угловыми скобками. Формат ввода целых и действительных чисел внутри скобок произвольный.
Координаты узлов исходной вычислительной сетки должны быть записаны в виде:
variables = "x", "y", "z"
zone f=point i= 17 j= 95 k= 66
//где на месте цифр должны стоять реальные размеры вычислительной сетки
Beginning (Ipr=0) or Continuation (Ipr=1) Ipr = <0>
Name of Large File Nlf = <M1>
Name of Small File Nsf = <M2>
Heat Ratio Cappa = < 1.4 >
Mach Number Me = <10.000>
Angle of Attack Alf = < 30.0 >
Altitude of Flight [km] Hf = < 0.0 >
Number of Intervals:
From Body to Shock Wave ( J0 <120 ) J0 = < 50>
Along the Rotation Angle ( K0 < 60 ) K0 = < 20>
Along the Body (Total) ( I0 <150 ) I0 = < 89>
Smoothness Coefficient of Shock Wave Surfase Sgl = < 0.25 >
Number of Steps with 1-nd Order Approximation Nst1 = < 9000000>
Number of Steps with Curant Number = 0.4 Nst2 = < 300>
Finish Step Number Nst3 = < 9000000>
Step Interval for Saving Record Nst4 = < 2000>
Body Sizes (Used for Cx, Cy, Cd, Mz Calculations Only). Middle Radius Rm = < 1.8>
Number of Steps with start Oscillate NKOL = < 2000>
Пример заполнения файла приведен ниже:
variables = "x", "y", "z"
zone f=point i= 17 j=95 k= 66
0.000000000000000E+000 0.000000000000000E+000 0.000000000000000E+000
-5.440973910234275E-002 0.000000000000000E+000 0.000000000000000E+000
-1.088194784046708E-001 0.000000000000000E+000 0.000000000000000E+000
-1.632292171070402E-001 0.000000000000000E+000 0.000000000000000E+000
-2.176389578092738E-001 0.000000000000000E+000 0.000000000000000E+000
-2.720486965116438E-001 0.000000000000000E+000 0.000000000000000E+000
-3.264584352140122E-001 0.000000000000000E+000 0.000000000000000E+000
-3.808681739163815E-001 0.000000000000000E+000 0.000000000000000E+000
-4.352779136186835E-001 0.000000000000000E+000 0.000000000000000E+000
-4.896876513211203E-001 0.000000000000000E+000 0.000000000000000E+000
-5.440973910234220E-001 0.000000000000000E+000 0.000000000000000E+000
-5.985071297257913E-001 0.000000000000000E+000 0.000000000000000E+000
-6.529168684281610E-001 0.000000000000000E+000 0.000000000000000E+000
-7.073266081304622E-001 0.000000000000000E+000 0.000000000000000E+000
Выходными данными программы являются файлы двух типов:
- графические файлы;
- файлы со значениями основных аэродинамических характеристик и координат узлов сетки.
0 1,20E+02 2,73E+00 -8,29E-01 2,96E-01 0,00E+00 1,56E+01 0,00E+00
0,004194 1,20E+02 2,73E+00 -8,29E-01 2,96E-01 8,00E+04 1,56E+01 -8,70E-05
0,00839 1,20E+02 2,73E+00 -8,29E-01 2,96E-01 8,00E+04 1,56E+01 -3,48E-04
0,012586 1,20E+02 2,73E+00 -8,29E-01 2,96E-01 8,00E+04 1,56E+01 -7,83E-04
0,016783 1,20E+02 2,74E+00 -8,30E-01 2,96E-01 8,00E+04 1,56E+01 -1,39E-03
0,020979 1,20E+02 2,74E+00 -8,31E-01 2,97E-01 8,00E+04 1,56E+01 -2,18E-03
0,029372 1,20E+02 2,74E+00 -8,32E-01 2,97E-01 8,00E+04 1,56E+01 -4,27E-03
0,033569 1,20E+02 2,75E+00 -8,33E-01 2,98E-01 8,00E+04 1,56E+01 -5,57E-03
0,037765 1,20E+02 2,75E+00 -8,33E-01 2,98E-01 7,99E+04 1,56E+01 -7,05E-03
0,041962 1,20E+02 2,75E+00 -8,34E-01 2,98E-01 7,99E+04 1,56E+01 -8,71E-03
0,046158 1,20E+02 2,75E+00 -8,35E-01 2,98E-01 7,99E+04 1,56E+01 -1,05E-02
0,050354 1,20E+02 2,76E+00 -8,36E-01 2,99E-01 7,99E+04 1,56E+01 -1,25E-02
0,058747 1,20E+02 2,76E+00 -8,37E-01 2,99E-01 7,99E+04 1,56E+01 -1,71E-02
0,062943 1,20E+02 2,76E+00 -8,38E-01 2,99E-01 7,99E+04 1,56E+01 -1,96E-02
0,06714 1,20E+02 2,77E+00 -8,39E-01 3,00E-01 7,99E+04 1,56E+01 -2,23E-02
0,071336 1,20E+02 2,77E+00 -8,39E-01 3,00E-01 7,99E+04 1,56E+01 -2,52E-02
0,079729 1,20E+02 2,77E+00 -8,41E-01 3,00E-01 7,99E+04 1,56E+01 -3,14E-02
0,083925 1,20E+02 2,78E+00 -8,42E-01 3,01E-01 7,99E+04 1,56E+01 -3,48E-02
0,088121 1,20E+02 2,78E+00 -8,42E-01 3,01E-01 7,99E+04 1,56E+01 -3,84E-02
0,092317 1,20E+02 2,78E+00 -8,43E-01 3,01E-01 7,99E+04 1,56E+01 -4,21E-02
0,096514 1,20E+02 2,78E+00 -8,44E-01 3,02E-01 7,99E+04 1,56E+01 -4,61E-02
0,10071 1,20E+02 2,79E+00 -8,45E-01 3,02E-01 7,99E+04 1,56E+01 -5,02E-02
…………………………………………………………………………
Здесь значения компонент скорости отнесены к модулю скорости набегающего потока, плотность – к плотности набегающего потока, давления – к удвоенному скоростному напору набегающего потока.
Пример содержания файла для визуализации PPROD:
VARIABLES = "X", "Y", "Ro", "P" "M"
ZONE F = POINT, I= 51 J= 179
9,08E+00 -8,62E+00 2,14E-02 1,15E+02 2,34E-01
9,07E+00 -8,63E+00 2,15E-02 1,15E+02 2,76E-01
9,06E+00 -8,66E+00 2,17E-02 1,15E+02 3,50E-01
9,05E+00 -8,67E+00 2,17E-02 1,15E+02 3,77E-01
9,03E+00 -8,68E+00 2,17E-02 1,14E+02 4,03E-01
9,01E+00 -8,72E+00 2,17E-02 1,13E+02 4,56E-01
8,99E+00 -8,74E+00 2,16E-02 1,12E+02 4,83E-01
8,98E+00 -8,76E+00 2,15E-02 1,11E+02 5,09E-01
8,96E+00 -8,78E+00 2,15E-02 1,11E+02 5,28E-01
Рассмотрим результаты программы.
Наши исходные данные для вычислений: α=30°, M=10, начальная высота 80 км.
На рис. 2-3 в качестве иллюстративного материала, представлены области распределения давления вблизи ступени при различных положениях относительно системы координат.
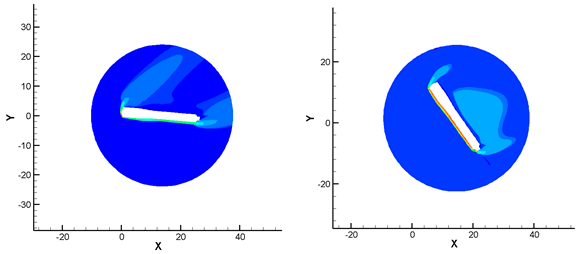
Рисунок 2. Распределение давление в расчетной области при числе Маха набегающего потока равное 10, при δ=5° и δ=55°
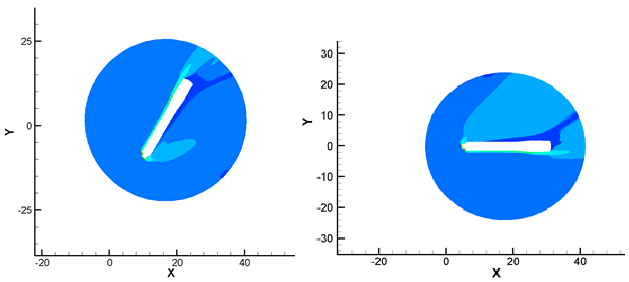
Рисунок 3. Распределение давление в расчетной области при числе Маха набегающего потока равное 10, при δ=120° и δ=180°
Результаты обработки t, δ, ρ, P, h, xc, yc представлены на рис. 4-6 в виде графиков зависимостей угла атаки от времени при колебании ступени при различных положениях ступени ракеты-носителя относительно системы координат (угла δ). Колебания несут затухающий характер.
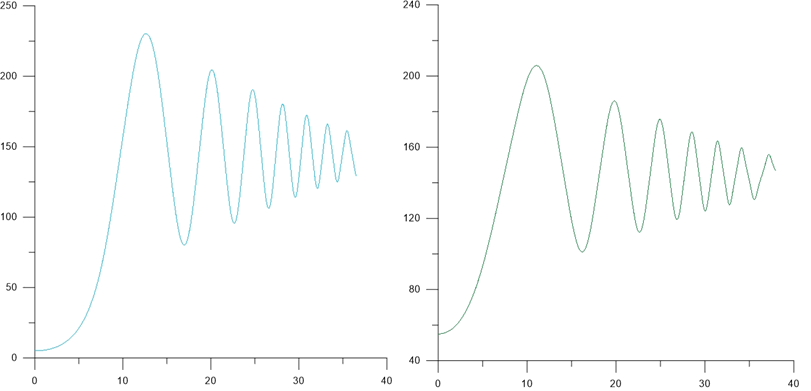
Рисунок 4. Зависимости δ от времени для угла δ=5° и δ=55°
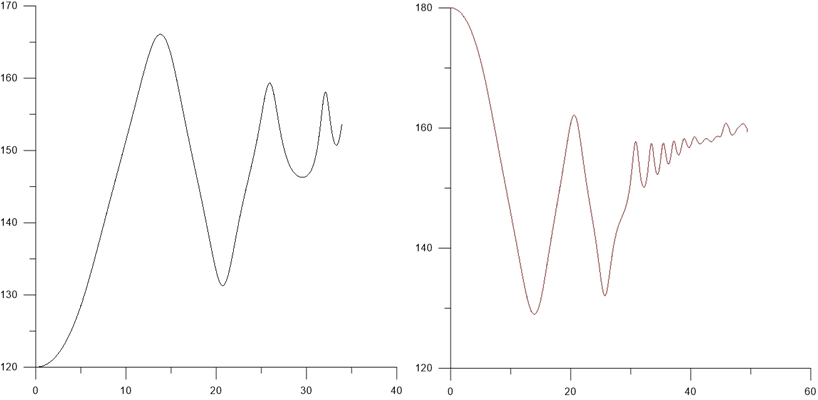
Рисунок 5. Зависимости δ от времени для угла δ=120° δ=180°
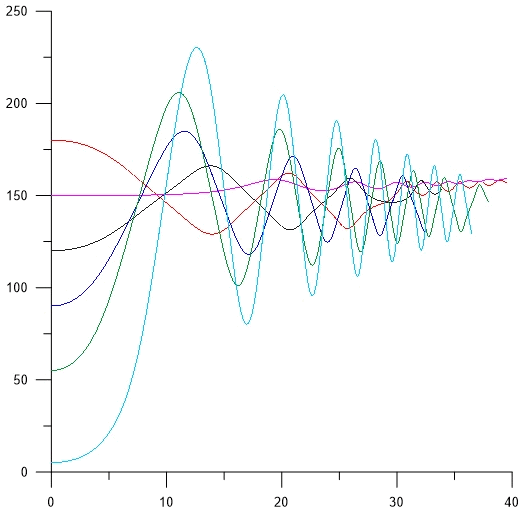
Рисунок 6. Зависимости угла отклонения δ от времени при колебаниях для различных углов δ
На рис. 7 ступень двигается относительно движущейся системы координат. Система координат движется с постоянной скоростью, а тело в этой системе обувается потоком. По оси Х видно, на какое расстояние относительно начало координат отдалилась ступень.
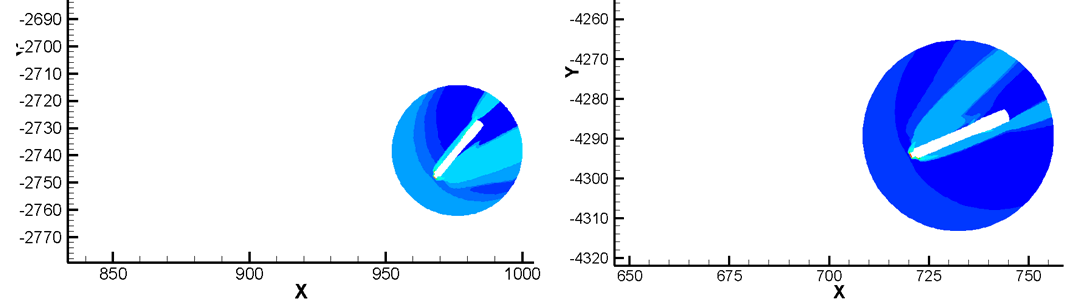
Рисунок 7. Движение относительно движущейся системы координат на высоте h=40 км, t=26.4сек и h=31,7 км, t=31сек
Ниже на рис. 8-9 показаны зависимости движение ступени по координате Xc от времени. Можно наблюдать как отклоняется ступень во время падения с высоты 80 км от начальной точки.
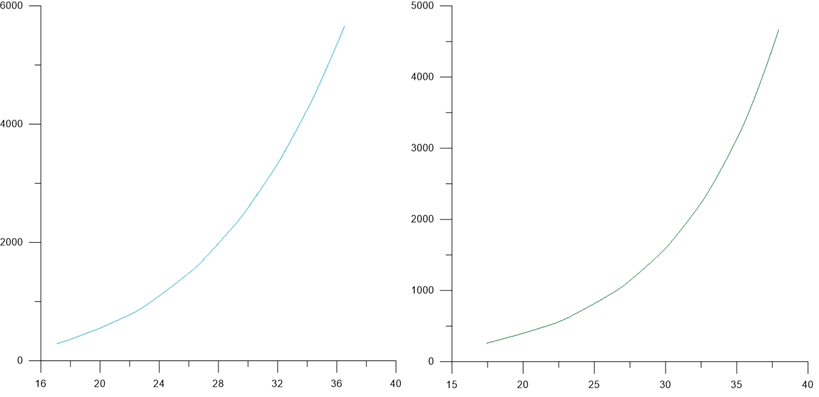
Рисунок 8. График движения зависимость Xc от t при начальном угле отклонение δ=5°и δ=55°
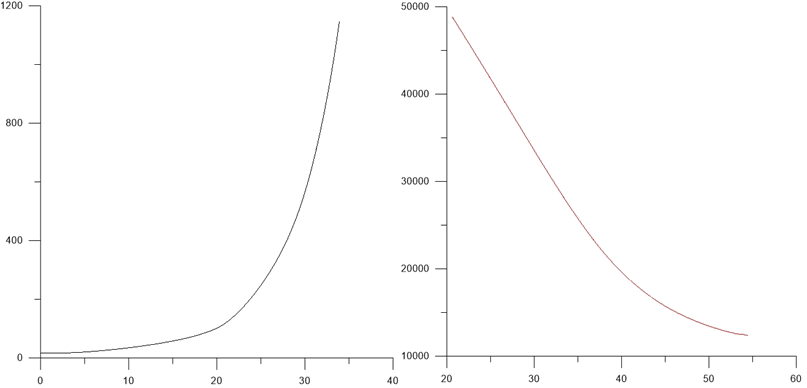
Рисунок 9. График движения зависимость Xc от t при начальном угле отклонение δ=120° и δ=180°
2-ая ступень в отличие от первой успевает за свое время работы набрать достаточно скорости и высоты, чтобы начать при падении разваливаться на десятки объектов. C помощью полученных результатов можно оценить размеры территории падения обломков ступени. Зона рассеивания обломков зависит от движения ступени и ее положении (угла отклонения δ).
Для определения области разброса обломков отработанных ступеней ракет-носителей, необходимо учитывать изменение плотности, за счёт того, что проседает система координат и движение относительно этой системы координат, которая движется с постоянной начальной скоростью.
Рассматривать ступень под разными углами ориентации (δ). Рассчитывать такие параметры, как t, δ, ρ, P, h, xc, yc с помощью которых, можно определить координаты падения и построить область разброса обломков.
Также вычислив давление, действующее при падении на ступень, можно определить аэродинамическую силу воздействующая на тело в любой момент его падения.
- Годунов С.К. и др. Численное решение многомерных задач газовой динамики. М.:"Hаука".1976.
- Родионов А.В. Численный метод решения уравнений Эйлера с сохранением аппроксимации на деформируемой сетке. ЖВМ и МФ. 1996. 36. №3. сс.117-129.
- Рахматулин Х. А., Сагомонян А. Я., Бунимович А.И., Зверев И. Н. Газовая динамика. Изд. «Высшая школа» 1965.
- J. Blazek. Computational Fluid Dynamics: Principles and Applications. Elsevier. 2005.
- Г. В. Липман, А. Рошко. Элементы газовой динамики. Перевод с английского В. П. Шидловского. Издательство иностранной литературы. Москва 1960.-505с.
- Липницкий Ю.М., Красильников А.В., Покровский А.Н., Шманенков В.Н. «Нестационарная аэродинамика баллистического полета», Москва, ФИЗМАТЛИТ, 2003.
- Дэниел Д. Мак-Кракен, Уильям С. Дорн. Численные методы и программирование на ФОРТРАНе. Ориг. название – Numerical Methods and Fortran Programming with Application in Engineering and Science, 1977.
Ключевые слова: Числа Маха, метода Эйлера, уравнение динамики, движение идеального газа, задачи Римана, схема Годунова, аппроксимация, Fortran, трехмерное обтекание, зона рассеивания.
Movement of launch vehicle stages for open alienation zones
Povalyayev P.P., Moscow Aviation Institute (National Research University), engineer
Kalenova N.V., Moscow Aviation Institute (National Research University), Associate Professor
Romanenkov A.M., Moscow Aviation Institute (National Research University), Associate Professor
Sharikov D.V., Moscow Aviation Institute (National Research University), engineer
Abstract: In this paper, we consider an approach that will allow us to investigate the movement of the stages of launch vehicles. For example, the launch of the Soyuz launch vehicle was considered, or rather the critical fall of the second stage. To develop recommendations for reducing the “alienation” zone, a method of numerical modeling of free oscillations of the model has been implemented. The basic program based on the Godunov – Rodionov method of integrating the non-stationary Euler equations was improved by adding the ordinary differential equation of plane body motion (including plane angular motion and center-of-mass motion) to the integration unit, taking into account changes in the parameters of the incident flow due to height changes. To solve the gas-dynamic problem, a program for constructing a three-dimensional structured computational grid, in a rectangular coordinate system, has been developed. Processed data and visualized in specialized software packages such as Tecplot and Grapher 2.0.
Keywords: Mach numbers, Euler method, dynamic equation, ideal gas motion, Riemann problem, Godunov scheme, approximation, Fortran, three-dimensional flow, scattering zone.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|











 ПОВАЛЯЕВ П.П., Московский авиационный институт (национально исследовательский университет), инженер
ПОВАЛЯЕВ П.П., Московский авиационный институт (национально исследовательский университет), инженер КАЛЁНОВА Н.В., Московский авиационный институт (национально исследовательский университет), доцент
КАЛЁНОВА Н.В., Московский авиационный институт (национально исследовательский университет), доцент
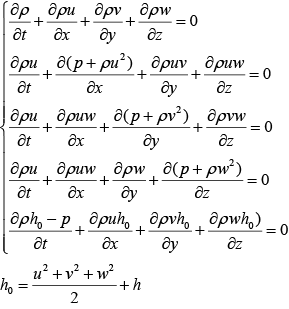 (1)
(1)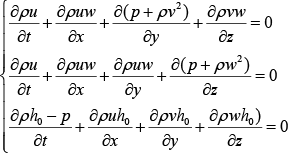 (20)
(20)













