|
Рубрика:
Наука и технологии /
Раздел для научных публикаций
|
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
 БОРИСОВ Н.И., д.т.н., профессор, Национальный исследовательский университет «Высшая школа экономики», Москва, nborisov@hse.ru
КАСАТКИН А.Д., инженер, Национальный исследовательский университет «Высшая школа экономики», Москва, adkasatkin@hse.ru
ПРЕСНЯКОВ С.А., ассистент, Национальный исследовательский университет «Высшая школа экономики», Москва, spresnyakov@hse.ru
Снижение трудоемкости вычислений
за счет настройки макромодели на диапазон расчета выходных характеристик схемы
Излагается формальный метод построения макромодели линейной эквивалентной электрической схемы, сформированной в однородном координатном базисе. По макромодели с одинаковой точностью, но с увеличенной на несколько порядков скоростью вычисления, могут проводиться те же расчеты, что и по исходной модели. Скорость многовариантного вычисления частотных характеристик может быть повышена за счет построения и редукции в каждой точке частотного диапазона системы линейных алгебраических уравнений
По модели схемы, построенной в расширенном координатном базисе
строится макромодель
 (1.1)
где Aij(p)=Cijp+Gij, i,j=1,2, X1 – (M×1)-вектор «внутренних» переменных; X2 – (m×1)-вектор «внешних» переменных схемы, отражающих соотношения типа «вход-выход» и, если необходимо, малое количество варьируемых параметров, содержащихся в малом количестве уравнений Q=(q1,...,qk)T, M>>m, m+M=N, p=jω,  , ω – круговая частота.
Ясно, что основной проблемой построения макромодели является вычисление в аналитическом виде матрицы A–111(p). Для этого необходимо вычислить все собственные значения и правые и левые собственные векторы матрицы A11(p)=C11p+G11.
При условии, что матрица C11p+G11 является регулярной, т.е. detG11≠0, вид обратной матрицы определяется следующим образом:
(C11p+G11)–1=B11(D11p+E11)–1ST11
где B11 – матрица правых собственных векторов, S11 – матрица левых собственных векторов, D11=–diag(λ–11,...,λ–1M), det(C11λi+G11)=0, i=1,M, E11 – единичная матрица соответствующего размера [1, 2, 3]. При этом длины правых илевых собственных векторов должны удовлетворять условию следующей нормировки:
ST11G11B11=E11
Подстановка вычисленной обратной матрицы в макромодель (1.1), а также перемножение окаймляющих обратную матрицу матриц на матрицы собственных векторов приводит к окончательному виду макромодели [4, 5]:
 (1.2)
Макромодель получена с учетом того, что rangC11=r<M. Вследствие этого левая верхняя диагональной матрицы (D11p+E11)–1 является единичной ранга r–M. Тогда U21, V21, U12, V12 – числовые вещественные (r×M) и (M×r)-матрицы соответственно, а матрицы V2, V1, V0 и векторы YM–r,1, YM–r,0 являются матрицами и векторами соответствующего размера.
Частотные характеристики могут вычисляться по макромодели (1.2) заменой буквы p на переменную Лапласа jω, а градиент выходной характеристики вычисляется тривиальным образом.
Трудоемкость построения макромодели примерно равна M4 вещественных мультипликативных операций (ВМО), т.е. трудоемкости вычисления собственных значений и векторов матрицы A11(p).
Трудоемкость вычисления одной точки частотных характеристик по макромодели состоит из двух частей:
- T1≈6mr+4m2r+3m2 ВМО – трудоемкость формирования числовой системы уравнений по макромодели;
- T2≈4m3/3+6m2 ВМО – трудоемкость решения комплексной системы линейных алгебраических уравнений с помощью нормализованного LQ – разложения с использованием матриц отражения.
Как видно из последних выражений, трудоемкость T1 существенно больше трудоемкости T2. В связи с этим по макромодели предлагается формировать и запоминать lx систем линейных алгебраических уравнений (СЛАУ) следующего вида:
 (1.3)
где Ai – числовая (m×m)-матрица с комплексными коэффициентами, Bi(Q) – (m×m)-буквенно-числовая матрица с комплексными коэффициентами, в которой буквами являются варьируемые параметры схемы. Вычисление функций чувствительности частотных характеристик осуществляется путем решения СЛАУ
Поскольку наиболее трудоемкие операции вычисления матриц проведены перед вычислением частотных характеристик, трудоемкость определения одной точки частотных характеристик по (1.3) становится пропорциональной только трудоемкости LQ-разложения комплексной (m×m)-числовой матрицы. Платой за резкое увеличение скорости вычислений является увеличение рабочего поля метода, поскольку необходимо хранить матрицы систем вида (1.3).
Рассмотренный численный метод был реализован в виде прикладных программ в рамках диалоговой системы моделирования, макромоделирования, анализа и оптимизации линейных эквивалентных электрических схем. Для тестового примера с характеристиками N=44, m=8, k=6, r=29, трудоемкость вычислений по макромодели по сравнению с (1.2) сократилась в 12 раз, а по сравнению с трудоемкостью вычисления частотных характеристик по модели – в 1200 раз. Значения вычисляемых по модели и макромодели характеристик совпадали в первых 16 цифрах после десятичной точки при использовании 20-разрядной десятичной мантиссы.
Дальнейшее снижение трудоемкости вычисления частотных характеристик может быть получено в результате преобразования СЛАУ (1,3), обеспечивающего снижение их размерности. Для этого модель, по которой строится макромодель, должна иметь вид, характеризующийся включением варьируемых параметров на диагонали матриц. Для объяснения сути преобразований, запишем какую-либо СЛАУ из (1.3) в блочном виде
 (1.4)
где XT2=(XT21,XT22,XT23), X21 – (nx×1)-вектор, содержащий выходные характеристики схемы, QT=(QT1,QT2), (k×1)-вектор варьируемых параметров схемы, m=nx+k, Q1, Q2 – ((k/2)×1)-подвекторы. Все подматрицы в матрице СЛАУ (1.8) – числовые комплексные, за исключением подматриц W22(Q1) и W33(Q2). Матрица W22(Q1)=T22+R22Q1 – ((k/2)×(k/2))-матрица, причем T22 – плотная комплексная числовая, R22 – диагональная комплексная, Q1 – диагональная буквенная, т.е. Q1=diag(q1,...,qk/2). Матрица W33(Q2) имеет аналогичный порядок и вид с той лишь разницей, что вместо матрицы Q1 используется матрица Q2.
Применяя к СЛАУ (1.4) для первых nx числовых столбцов преобразования Жордана-Гаусса, а для следующих k/2 столбцов операции исключения Гаусса снизу вверх, масштабируя матрицу на каждом шаге исключения по коэффициентам многочленов от qi, выбираемых по всей матрице, получим преобразованную СЛАУ в виде
где  – единичная (nx×nx)-матрица,  – (nx×(k/2))-матрица, V0, V1 – плотные комплексные матрицы,   – ((k/2)×(k/2))-матрица, U0, U1, U2, U3 – плотные комплексные числовые матрицы,  ,  и  – числовые векторы соответствующего размера.
Таким образом, для вычисления выходных характеристик X21 при каждом новом значении вектора варьируемых параметров Q необходимо вычислить и решить преобразованную СЛАУ вида
 (1.5)
 (1.6)
Определение функций чувствительности частотных характеристик проводится путем решения СЛАУ
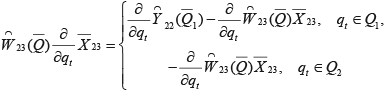
Для решения систем (1.5), (1.6) требуется примерно
вещественных мультипликативных операций, что существенно меньше, чем в ранее приведенных формулах. Трудоемкость вычислений по (1.5), (1.6) сокращается по сравнению с трудоемкостью вычислений по (1.3) не менее чем в 8r/m раз. Эффективность рассмотренного подхода тем больше, чем меньше величина отношения k/nx.
Так, для рассмотренного выше примера трудоемкость вычисления частотных характеристик по СЛАУ (1.5), (1.6) сократилась по сравнению с трудоемкостью решения СЛАУ (1.3) в 4 раза, а по сравнению с трудоемкостью аналогичного анализа модели – в 4800 раз. При этом точность вычисления частотных характеристик не снизилась. Их значения, вычисленные по модели и соответствующему множеству преобразованных СЛАУ вида (1.5), (1.6), совпадали по первым 16цифрам при использовании 20-разрядной десятичной мантиссы.
Трудоемкость преобразования систем (1.4) фактически пропорциональна их однократному решению. Для рассмотренного выше примера с помощью диалоговой системы моделирования, макромоделирования, анализа и оптимизации эквивалентных электрических схем решалась задача параметрической оптимизации в частотной области.
При вычислении 80 точек частотных характеристик для построения систем вида (1.5), (1.6) по макромодели (1.3) потребовалась примерно 1 секунда, после чего для проведения 100 шагов поиска локального экстремума целевой функции градиентным методом оптимизации Флетчера-Ривса потребовалась примерно 1 секунда машинного времени.
В заключение отметим, что переход от систем (1.3) к системам вида (1.5), (1.6) не только сокращает трудоемкость вычислений, но и уменьшает рабочее поле метода. По сравнению с (1.3) экономия составляет nx∙lx∙m ячеек памяти компьютера.
Статья подготовлена в ходе/в результате проведения исследования/работы (№ 19-04-005) в рамках Программы «Научный фонд Национального исследовательского университета „Высшая школа экономики“ (НИУ ВШЭ)» в 2019-2020 гг. и в рамках государственной поддержки ведущих университетов Российской Федерации «5-100».
- The Sixth China-Russia Conference on Numerical Algebra with Applications (CRCNAA 2017) (Москва). Доклад: Macromodeling of linear equivalent electrical circuits.
- Борисов Н.И., Малина А.С. Разработка методов определения частотных свойств линейных электрических эквивалентных с использованием макромоделирования. // «Качество. Инновации. Образование», № 3, 2013 г. – С. 44-49.
- Абрамешин А.Е., Борисов Н.И., Кравченко Н.П., Малина А.С. Метод иерархического макромоделирования в задачах анализа линейных электрических эквивалентных схем в САПР. // «Качество. Инновации. Образование», № 11, 2013 г.– С. 40-46.
- Борисов Н.И., Востриков А.В., Кравченко Н.П., Малина А.С. Разработка метода редукции модели линейной эквивалентной электрической схемы, построенной в однородном координатном базисе. // «Технологии электромагнитной совместимости», № 4, 2014 г. –С. 49-57.
- Борисов Н.И. Исследование и разработка методов снижения размерности и трудоемкости задач анализа и оптимизации линейных эквивалентных электрических схем на основе макромоделирования в САПР. Автореферат диссертации на соискание ученой степени доктора технических наук. – М., 1996.
Ключевые слова: макромодель, эквивалентная электрическая схема, частотные характеристики.
Reducing the complexity of calculations due to setting the macromodel on the calculation range of the scheme output characteristics
Borisov N.I., D.Sc., Professor, National Research University Higher School of Economics, Moscow, nborisov@hse.ru
Kasatkin A.D., Engineer, National Research University Higher School of Economics, Moscow, adkasatkin@hse.ru
Presnyakov S.A., Assistant, National Research University Higher School of Economics, Moscow, spresnyakov@hse.ru
Abstract: A formal method for constructing a macromodel of a linear equivalent electrical circuit formed in a uniform coordinate basis is described. The macromodel with the same accuracy, but with the calculation speed increased by several orders of magnitude, can be applied for the same calculations as the original model. The speed of multivariate calculation of frequency characteristics can be increased by building and reducing of a system of linear algebraic equations at each point of the frequency range.
The article was prepared within the framework of the Academic Fund Program at the National Research University Higher School of Economics (HSE) in 2019-2020 (grant № 19-04-005) and by the Russian Academic Excellence Project «5-100».
Keywords: macromodel, equivalent electrical circuit, frequency characteristics.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
Снижение трудоемкости вычислений за счет настройки макромодели на диапазон расчета выходных характеристик схемы
