|
Рубрика:
Наука и технологии /
Раздел для научных публикаций
|
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
 ТУМАНОВ М.П., к.т.н., профессор (НИУ ВШЭ, МИЭМ), Москва, miketum@mail.ru ТУМАНОВ М.П., к.т.н., профессор (НИУ ВШЭ, МИЭМ), Москва, miketum@mail.ru
Устойчивость распределенных систем
автоматического управления при нелинейном запаздывании
В статье показано, что в типовой системе автоматического управления, содержащей сетевую компоненту, возможно как падение запаса устойчивости за счет сетевого запаздывания, так и в некоторых случаях увеличение этого запаса. В статье рассмотрены типовые характеристические уравнения и вычислены их корни в зависимости от запаздывания. Результаты вычислений подтверждены моделированием в среде Matlab
Рассмотрим следующую модель распределенной системы автоматического управления, сигналы в которой передаются по сети, расположенной в значительном по протяженности пространстве через множество узлов (коммутаторов) (см. рис. 1).
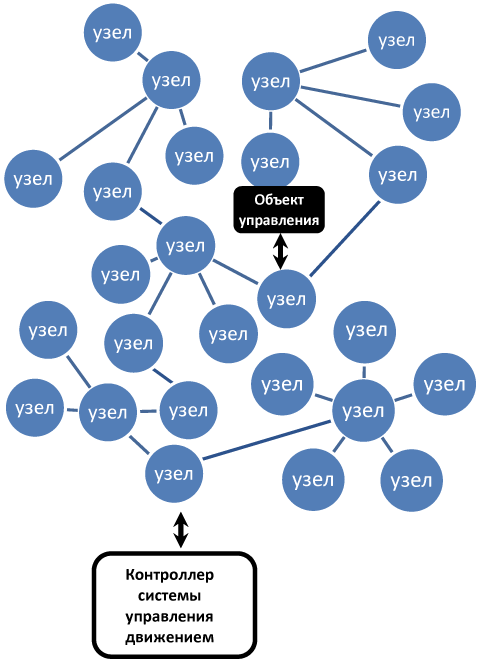
Рисунок 1. Распределенная система управления с движущимся в сети объектом
Между контроллером и объектом управления установлено сетевое соединение, по которому передается вся телеметрия и сигналы управления.
При движении объекта управления (ОУ) происходит передача точки подключения ОУ к сети и изменяется при этом основной рассматриваемый в статье параметр – время доставки сообщений.
Будем считать также (для простоты), что функция, выражающая зависимость времени доставки сообщения от положения в физическом пространстве детерминирована и хорошо определена. В частности, просто линейно зависит от длины пути. Таким образом, двигаясь в физическом пространстве, объект также перемещается и в виртуальном сетевом пространстве. Система управления неизбежно должна это учитывать.
С точки зрения теории управления имеется система с переменным запаздыванием, зависящим от координат объекта. Далее рассмотрим одну из простейших, но вполне правдоподобных моделей, в которой время запаздывания линейно зависит от расстояния от начала координат, которое соответствует невозмущенному движению:
τ(t,x)=τ0+d∙|x(t)| (1)
Здесь:
- τ(t,x) – текущее запаздывание, неотрицательно;
- τ0 – постоянное запаздывание, может быть нулевым;
- d – числовой коэффициент.
Рассмотрим типовую систему, уравнение состояния которой записаны относительно величины x(t). Без учета помех и возмущений имеем вид:
 (2) (2)
Это уравнение нелинейно, так как аргумент x зависит от него самого. Если бы даже эта зависимость была линейной, все равно в целом уравнение было бы нелинейным дифференциальным уравнением. В контексте систем управления такие уравнения практически не изучены, кроме, пожалуй, [1].
В то же время известно, что в настоящих нелинейных системах (например, с гистерезисом или переменной структурой) возможны сложные, чисто нелинейные эффекты, которые никогда не возникают в линейных системах.
Среди таких эффектов – предельные циклы и квазихаос.
Отдельный интерес представляют методы расчета устойчивости и качества в подобных системах с уравнениями типа (2). В частности, нахождение границ устойчивости, для чего при этом неприменимы обычные методы (кроме методов функций Ляпунова) вследствие нелинейности.
Промоделируем систему третьего порядка, чтобы изучить характерные случаи. На рис. 2 приведена схема Matlab/Simulink для моделирования этой системы. Это позволяет изучить влияние на устойчивость:
- коэффициентов модели;
- величин запаздывания;
- диапазона и знака изменения запаздывания;
- начального состояния.
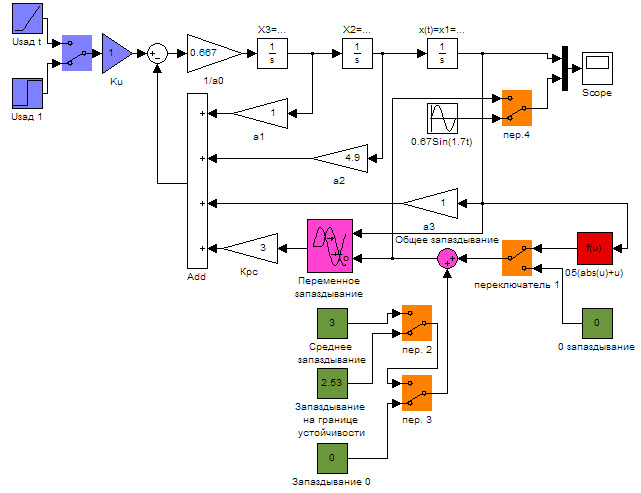
Рисунок 2. Моделирование системы с запаздыванием в Matlab/Simulink
Выбраны следующие коэффициенты (3) для модели (2):
1.5x(t)(3)+1.0x(t)(2)+4.9x(t)(1)+1.0x(t)=3.0(Uзад(t)–x(t–τ(t,x)))=K(Uзад(t)–x(t–τ0–d∙|x(t)|)) (3)
При заданных коэффициентах характеристическое уравнение (без учета переменного запаздывания) имеет вид (4).
Pзс(p)=1.5p3+p2+4.91p+1+3exp(–τ0p) (4)
Общий вид этого уравнения: Pn(p)=Qm(p)exp(–τ0p).
При этом переключатель 1 находится в нижнем положении, а переключатели 0 и 1 задают постоянное запаздывание. Переменного запаздывания при этом нет.
При 0 запаздывании система неустойчива, корни характеристического уравнения (4) при этом: p1=–0.792, p2,3=+0.063±1.834i. Устойчивость не зависит от начального состояния, при выбранном начальном состоянии: x(0)=1; ẋ=1; ẍ=–1 имеет переходный процесс, см. рис. 3.
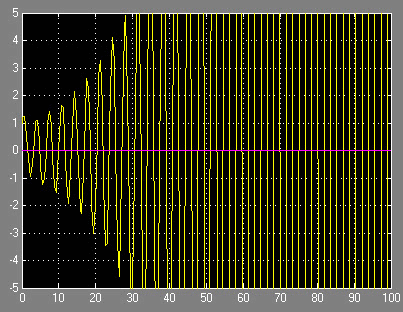
Рисунок 3. Замкнутая система при 0 запаздывании
Данная система интересна тем, что у нее есть область устойчивости, наступающая при τ0≈0.85 с корнями p2,3≈±1.37i и третьим вещественным корнем: p3≈–1.953, продолжающаяся до τ0≈2.5 с корнями p2,3≈±0.71i. Далее система снова неустойчива. Частоты колебаний на границе устойчивости уменьшаются при этом примерно в 4 раза, что хорошо видно на рис. 4-6.
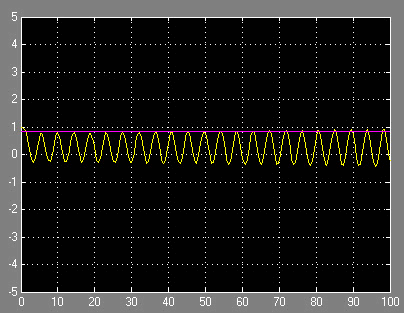
Рисунок 4. Замкнутая система при τ0≈0.85
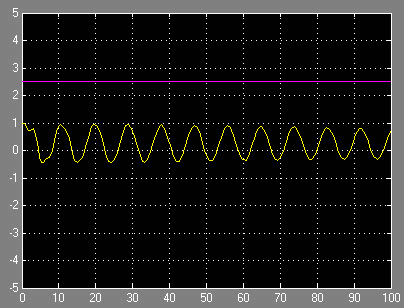
Рисунок 5. Замкнутая система при τ0≈2.5
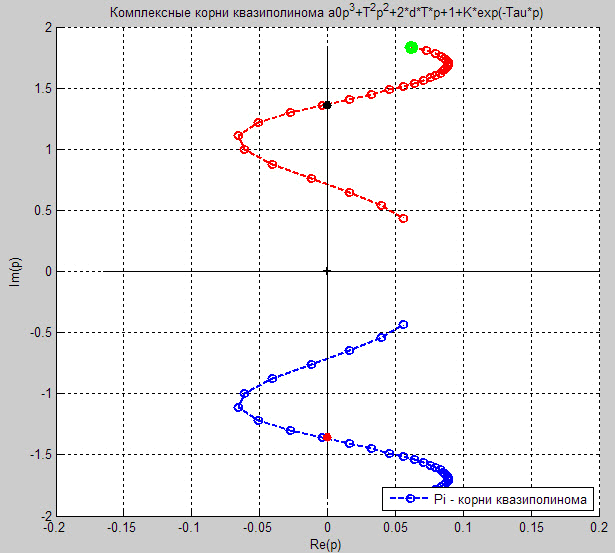
Рисунок 6. Корневой годограф при возрастании τ0. Жирная точка: τ0=0
Во всех этих случаях устойчивость не зависит от начального состояния и/или задающего воздействия. В линейной системе с постоянным запаздыванием может быть не более n – порядок системы частот на границе устойчивости [2]. Все они удовлетворяют полиномиальному уравнению порядка 2n вида:
|Pn(iω)|2=|Qm(iω)|2 (5)
которое в нашем случае имеет вид:
0.25ω6–13.7300ω4+22.1081ω2–8.000=0
Частоты на границе устойчивости (частота ω1 не реализуется ни при каком τ0):
ω1=1.9274; ω2=1.3703; ω3=0.71397
Вычислим граничные значения постоянного запаздывания из условия баланса фаз:
φ(iω*)–iω*τ0=–π
Теперь введем в систему переменное запаздывание (1) по формуле (6):
τ(t,x)=τ0+|x(t)| (6)
Сразу обнаруживается автоколебательный режим с амплитудой колебаний и частотой: а≈0.6; ω≈1 при τ0=0 (см. рис. 7). То, что это действительно автоколебания, очевидно при изменении начального условия (см. рис. 8-9).
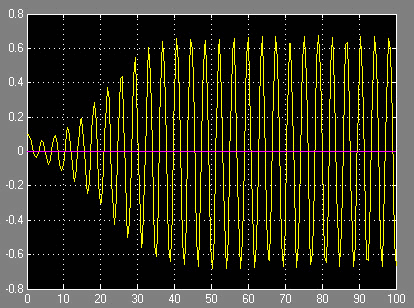
Рисунок 7. Автоколебательный режим при нелинейном запаздывании. x(0)=0.1
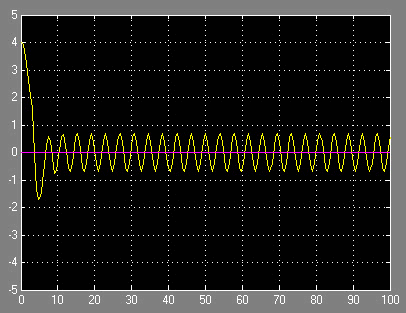
Рисунок 8. Автоколебательный режим при нелинейном запаздывании. x(0)=4
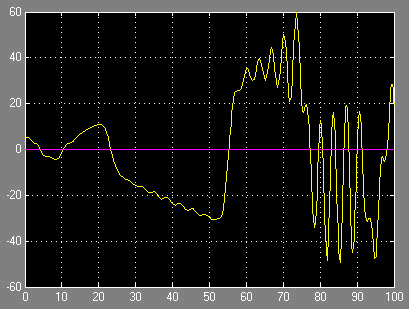
Рисунок 9. Автоколебательный режим при нелинейном запаздывании. x(0)=5.5
Также нелинейные свойства системы проявляются при подаче задающего воздействия в совокупности с нелинейным запаздыванием. На рис. 9 видно, что при начальном условии ~5 и более система теряет устойчивость и переходит к хаосу.
На рис. 10 также видна потеря устойчивости и переход к квазислучайным колебаниям при линейно-нарастающем задающем воздействии.
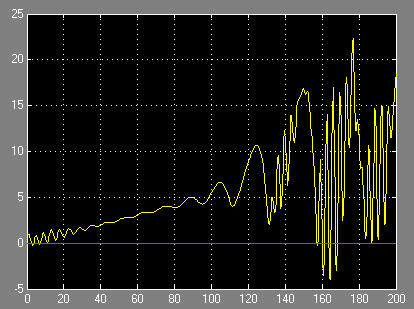
Рисунок 10. Потеря устойчивости при линейно-нарастающем воздействии
Оставшаяся часть статьи посвящена вычислению амплитуды и частоты автоколебаний в такой системе. Применим для этого метод гармонической линеаризации нелинейного запаздывания [3]. Для систем подобного вида ранее этот метод, по-видимому, не применялся, хотя он эффективно используется применительно к схожим системам с гистерезисом. Заметим, что в нашем случае применение метода сулит быть эффективным, так как форма сигнала на выходе нелинейного элемента действительно близка к гармонической.
Выделим первую гармонику на выходе нелинейного элемента с учетом постоянной составляющей.
Так как
 (7) (7)
то можно выделить основную (первую) гармонику:
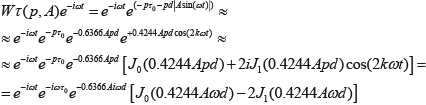 (8) (8)
Здесь Jn(z) – функции Бесселя 1-го рода.
Оценим погрешность отбрасывания части ряда:
R2<4/(3.1416*1.41*15)≈0.045
здесь R2 – оценка отбрасываемых членов ряда (7) начиная с номера k=2.
Таким образом, нелинейное запаздывание оказывается эквивалентным дополнительному запаздыванию, зависящему от амплитуды и частоты.
Теперь возможно вычислить амплитуду автоколебаний из условия гармонического баланса:
W(iω*)Wτ(iω*,A,τ0)=–1 (9)
Это есть необходимое условие, при котором система попадает на границу устойчивости и из этого условия получена связь между A, d и ω*. Эти А и ω* следует трактовать, как амплитуду и частоту автоколебаний.
Попытаемся ограничиться лишь 0 членом приближения (8). В этом приближении эффект нелинейности отграничивается дополнительным постоянным запаздыванием e–0.6366Adiω.
Так как |Wτ(iω*,A,τ0)|≡1, то частота будет зависеть только от линейной части системы и определяться тем же уравнением (5). Амплитуда определится из условия фазового сдвига –π (необходимое условие):
φ(iω*)–0.6366Adω*=–π (10)
Вычисление в среде Matlab дает три возможных решения:
- ω1=1.9274; A1=4.7626;
- ω2=1.3703; A2=1.4604;
- ω3=0.71397; A3=3.8172
Ошибка вычисления амплитуды автоколебания слишком высока, расчеты не достоверны. Нет соответствия рис.7-8. Используем полное уравнение (8-9). При этом его проблематично решить численным методом относительно неизвестных A и ω. Причина – недостаточная острота пика функции модуля АФЧХ, что видно на рис. 11. Поэтому воспользуемся 3D-графикой и логарифмическими координатами.
На рис. 11-13 приведены трехмерные графики логарифма модуля (ЛАЧХ, условие Найквиста нахождения на границе устойчивости).

Рисунок 11. Условие (9) при нелинейном запаздывании и обычном масштабе

Рисунок 12. Условие (9) при линейном запаздывании

Рисунок 13. Условие (9) при нелинейном запаздывании
Поворачивая 3D-график в пространстве, найдем его положение, при котором расположение минимумов становится очевидным. Например, на рис. 14 приведено положение графика для определения амплитуды возможных автоколебаний.
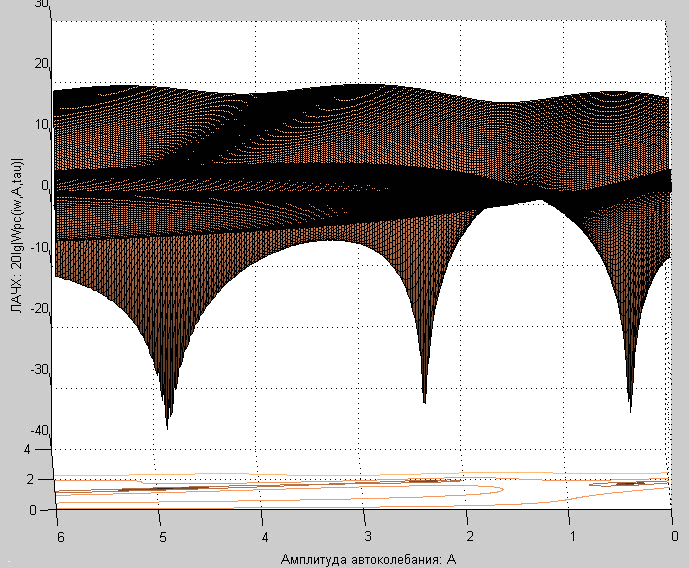
Рисунок 14. Удобный поворот графика рис. 13
Обнаруживаем возможность возникновения автоколебаний с A≈0.5; A≈2.4; A≈4.9. В силу того, что условия (9) лишь необходимые, надо отобрать реальные режимы. Их два: A≈0.5 есть устойчивый предельный цикл и A≈4.9 – неустойчивый цикл с переходом в квазихаос. Амплитуда реальных колебаний несколько выше, так как форма колебаний лишь приближена к гармонической. На рис. 15 сравнены синус соответствующей амплитуды и автоколебания.
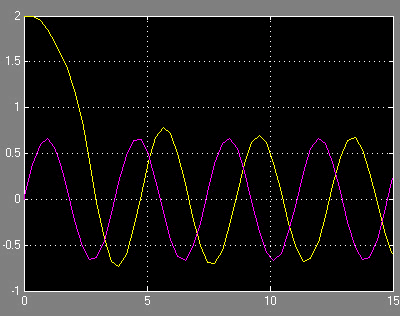
Рисунок 15. Синус соответствующей амплитуды и автоколебания
При наличии постоянного запаздывания τ0>0 амплитуда предельного цикла уменьшается до 0 при τ0→~1. Это легко увидеть при моделировании в Simulink. Но это также четко видно и из (8-9). На рис. 16 приведен график (9) при τ0=1. Очевидно, что амплитуда колебания равна 0.

Рисунок 16. Условие (9) при нелинейном запаздывании и τ0=0
Замечание: все графики построены в результате вычислений в среде Matlab численным методом Ньютона и методом Рунге-Кутта 4-го порядка с проверкой сходимости и точностью вычислений (абсолютной) 1е-6. Для гарантирования нахождения далеко расположенных корней квазиполинома использовано изменение начального приближения в комплексной плоскости в широких пределах.
- Системы с авторегулируемым запаздыванием. / С.Б.Норкин./ Монография на правах рукописи. – М., 2001, – 134 с.
- Эльсгольц Л.Э., Норкин С.Б. Введение в теорию дифференциальных уравнений с отклоняющимся аргументом. – М.: Наука, 1971. – 296 с.
- Попов Е.П. Прикладная теория процессов управления в нелинейных системах. М.: Наука, 1973. – 584 с.
Ключевые слова: распределенная система управления, запаздывание, компенсация.
The stability of the distributed automatic control systems with nonlinear delay
Tumanov M.P., Cand. of Techn. Sciences, professor (MIEM HSE), Moscow, miketum@mail.ru
Abstract: The article shows that in a typical automatic control system containing a network component, it is possible both to reduce the stability margin due to network lag and, in some cases, to increase this margin. The article deals with typical characteristic equations and their roots are calculated depending on the delay. The results of calculations are confirmed by simulation in Matlab.
Keywords: distributed control system; delay compensation.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
