|
Рубрика:
Наука и технологии /
Раздел для научных публикаций
|
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
 ОРУДЖЕВ Э.Г., доктор физико-математических наук, профессор, заведующий кафедрой математической экономики Бакинского государственного университета, Азербайджанская Республика, elsharorucov63@mail.ru ОРУДЖЕВ Э.Г., доктор физико-математических наук, профессор, заведующий кафедрой математической экономики Бакинского государственного университета, Азербайджанская Республика, elsharorucov63@mail.ru
 АЛИЕВ С.А., Нахичеванский институт учителей, кафедра высшей математики и информатики, старший преподаватель, Азербайджанская Республика, sahil.liyev83@mail.ru АЛИЕВ С.А., Нахичеванский институт учителей, кафедра высшей математики и информатики, старший преподаватель, Азербайджанская Республика, sahil.liyev83@mail.ru
Исследование спектра и резольвенты
одного дифференциального пучка четвертого порядка с трехкратным характеристическим корнем
В работе в пространстве L2(0;∞) исследуются спектр и резольвента пучка дифференциальных операторов четвертого порядка, когда главный характеристический полином имеет один трехкратный корень. Показано, что пучок может иметь воткрытой нижней и открытой верхней полуплоскостях конечное или счетное число собственных значений, а непрерывный спектр заполняет всю действительную ось, где могут находиться спектральные особенности. Доказано, чторезольвента пучка является ограниченным интегральным оператором, определенным на всем пространстве L2(0;∞), с ядром типа Карлемана
В проcтранстве L2(0;∞) рассмотрим пучок дифференциальных операторов Lαλ, порожденный дифференциальным выражением:
 (1) (1)
и граничным условием:
 (2) (2)
где λ – спектральный параметр, r(x), p(x), q(x) – комплекснозначные функции, определенные и непрерывные на [0;∞), соответственно имеют непрерывные производные до порядка 3, 4, 5 включительно, сходятся интегралы
 (3) (3)
αvk, v=1,3, k=0,3 – фиксированные комплексные числа, такие, что формы Uv(Y) линейно независимы, число граничных условий меняется в зависимости от местонахождения параметра λ в комплексной плоскости.
Спецификой пучка Lαλ является то, что главный характеристический многочлен уравнения (1) имеет трехкратный корень i и простой корень i. В общем случае кратных корней этого многочлена формальные решения уравнения сполиноминальным вхождением λ могут содержать дробные степени параметра как в показателе экспоненты, так и при множителе экспоненты, и сама структура асимптотических представлений не только зависит от старших коэффициентов, но и алгебраических комбинаций при низких степенях параметра [1]. Здесь учтены эти свойства таким образом, что формальные решения не содержали дробные степени параметра.
Прямые спектральные аспекты обыкновенных дифференциальных операторов на конечном отрезке в случае различных корней главного характеристического многочлена изучены достаточно хорошо. Наиболее полные исследования различных спектральных аспектов проведены в работах Г.Д. Биркгофа, Я.Д. Тамаркина, М.А. Наимарка, М.В. Келдыша, А.Г. Костюченко, В.А. Ильина, В.А. Марченко, М.Г. Гасымова, М.Л. Расулова, А.А. Шкаликова и др.
В частности, вопросы кратной полноты системы собственных и присоединенных функций подобных пучков решены в зависимости от расположения этих корней. При этом существенным условием кратной полноты является расположение характеристических корней на различных лучах, исходящих из начала координат. При нарушении этого условия данная система присоединенных функций обладает бесконечным дефектом в смысле кратной полноты [2, 3, 4].
Дифференциальные пучки, заданные на бесконечных интервалах, также изучены довольно хорошо в случае различных характеристических корней. И здесь обнаружен такой эффект, что число граничных условий на левом конце в случае полуоси также зависит от местонахождения параметра λ и связано с расположением корней характеристического полинома, и соответствующий несамосопряженный пучок не является аналитической функцией параметра λ во всей комплексной плоскости [5, 6], но является аналитической функцией от λ в верхней и нижней полуплоскостях с разрезом вдоль вещественной оси.
Ввиду того, что рассматриваемый здесь пучок имеет один трехкратный характеристический корень, а это означает, что все они лежат на одном луче, выходящем из начала координат, а второй корень на противоположном луче относительно начала координат, надо провести специальное исследование этого пучка.
Когда имеются характеристические кратные корни, но они симметрично расположены относительно начала координат, соответствующие результаты о разложении по собственным функциям непрерывных и дискретных спектров получены вработах [7, 8, 9].
В работах [10, 11] исследовано уравнение (1) и построены операторы преобразования, переводящее решения уравнения:

на решения уравнения (1).
В частности, в [11] получено, что уравнение (1) имеет фундаментальную систему решений Yj(x,λ), j=1,4, которые удовлетворяют условиям:
 (4) (4)
существуют ядра K±j(x,t), такие, что
 (5) (5)
При этом K±j(x,t), j=1,4 удовлетворяют уравнениям
 (6) (6)
и имеет место
 (7) (7)
кроме того, функции K±j(x,t) и их производные удовлетворяют определенным интегральным условиям на характеристике t=x.
В данной работе исследуется структура спектра пучка Lαλ, строится ядро ее резольвенты и изучаются аналитические свойства ядра.
Заметим, что для пучка Lαλ не удается применить технику работы [5] в том отношении, что применяемый там подход предельного перехода при b→∞ для оператора Lαλ, порожденного дифференциальным выражениям (1) в конечном интервале (0,b) и некоторыми регулярными распадающимися краевыми условиями на концах этого интервала. Ввиду того, что эти краевые условия являются нерегулярными в смысле работы [1] для пучка Lαλb с привлечением тонких свойств оператора Lαλb, таких как, например, поведение ядра резольвенты (Lαλb)-1 при b→∞ вне малой окрестности спектра, не позволительно использовать этот подход при выводе интегрального представления резольвенты пучка Lαλ.
Сначала изучим структуру дискретного спектра пучка Lαλ. Обозначим через D совокупность всех функций Y(x,λ)∈L2(0,∞), таких, что:
- производные Y(v)(x,λ), v=0,3 существуют и абсолютно непрерывны в каждом конечном интервале [0,b], b>0 при каждом λ:±İmλ≥0;
- l(x,d/dx,λ)Y∈L2(0,∞)
Далее через Dα обозначим совокупность тех функций из D для которого выполняются условия (2). Определим Lαλ так: его область определения есть Dα и Lαλ=l(x,d/dx,λ)Y при Y∈D.
Обозначим A(λ)=det||Ui(Yk)||3i,k=1 и рассмотрим верхнюю полуплоскость λ:±İmλ≥0. В открытой ее части решения Yk(x,λ), k=1,3 принадлежат пространству L2(0,∞), а Y4(x,λ)∈L2(0,∞).
Если λ находится в открытой нижней полуплоскости, ни одно из решений Yk(x,λ), k=1,3 не принадлежит этому пространству, а Y4(x,λ)∈L2(0,∞).
Тогда собственные значения пучка Lαλ в открытой верхней полуплоскости определяются из уравнения A(λ)=0.
Собственные значения этого пучка в открытой нижней полуплоскости могут определяться одним краевым условием Uv(Y4)=0 где v может быть одно из чисел 1, 2, 3. А на действительной оси ни одно из решений Yk(x,λ), k=1,4 непринадлежит пространству L2(0,∞), следовательно, при İmλ=0 не одно из краевых условий не входит в Dαλ. Значит, на действительной оси пучок дифференциальных операторов Lαλ не имеет собственных значений. Действительно, если фиксируем λ0 с İmλ=0 и будем считать, что оно является собственным значением, тогда для решений из İmλ≥0 будем иметь  и Y(x,λ0)∈L2(0,∞), при этом хотя бы одно из чисел Ck, k=1,3 должно быть отлично от нуля. Но при x→∞ имеем и Y(x,λ0)∈L2(0,∞), при этом хотя бы одно из чисел Ck, k=1,3 должно быть отлично от нуля. Но при x→∞ имеем

Поэтому
 (8) (8)
Если Y(x,λ)∈L2(0,∞) тогда все Ck, k=0,2 должны равняться нулю, т.е. Y(x,λ0)=0, а это означает, что соответственно к λ0 не существует нетривиального решения.
Приближаясь к действительной оси из открытой нижней полуплоскости и при условии, что Y4(x,λ)∈L2(0,∞), Yk(x,λ)∈L2(0,∞), k=1,3, İmλ<0, подобным образом проверяется, что на действительной оси не имеются собственные значения.
Теперь предположим, что λ0 является точкой открытой верхней и открытой нижней полуплоскостей.
Теорема 1. Для того чтобы λ:±İmλ>0 являлась собственным значением пучка Lαλ, необходимо и достаточно, что A(λ0)=0.
Доказательство. Необходимость. Предположим, что число λ0 из открытой верхней полуплоскости является собственным значением оператора Lαλ. Тогда решение уравнения (1), принадлежащего пространству L2(0,∞), является линейной комбинацией решений Yk(x,λ0), k=1,3:
 (9) (9)
здесь Ci, i=1,3 – определенные коэффициенты. С другой стороны, Y(x,λ0), как решение уравнения (1) из L2(0,∞), должен удовлетворить краевые условия (2).
Подставляя (9) в (2) получаем:
 (10) (10)
Для того чтобы (10) имело ненулевое решение относительно Ck, k=1,3 должно быть A(λ0)=0.
Достаточность. Предположим, что A(λ0)=0. Тогда система (10) имеет нетривиальную систему решений {C1,C2,C3} причем |C1|+|C2|+|C3|≠0. Разрешая систему (10), затем подставляя найденные решения в (9), находим функцию Y(x,λ0)∈Dλ, для которой l(x,d/dx,λ)Y=0, т.е. является собственным значением пучка Lα. Теорема доказана.
Подобным образом получаем, что в открытой нижней полуплоскости имеются собственные значения, которые являются корнями уравнения B(λ)≡Uv(Y4)=0, где v – одно из чисел 1, 2, 3.
Теорема 2. Оператор Lαλ в открытой верхней и в открытой нижней полуплоскостях имеет собственные значения, которые являются соответственно корнями уравнения A(λ)=0 и B(λ)=0. Этот оператор не имеет собственных значений на действительной оси. Если числа λ0 и λ1 с İmλ0=0 и İmλ1=0, соответственно корни уравнения A(λ)=0 и B(λ)=0, тогда эти числа являются спектральными особенностями пучка Lαλ.
Доказательство. Предположим, что λμ является собственным значением пучка Lαλ. Тогда соответствующая собственная функция определяется из формулы

Положим, C3=1. Тогда из краевых условий (2) находим:
 (11) (11)
Ввиду того, что мы ищем ненулевые решения, ранг этой системы должен быть меньше 3. Пусть rang=2.
Тогда при условии, что

можно из системы
 (12) (12)
определить Ci, i=1,2. Для них Ci=–Δi(λ)/Δ0(λ), i=1,2. Здесь Δi(λ) получается из Δ0(λ) заменой элементов столбца с номером i на элементы {–U1(Y3),–U2(Y3)}'.
Таким образом, собственная функция, отвечающая собственному значению λμ, выражается формулой
 (13) (13)
Непосредственным вычислением с использованием формулы Лейбница для дифференцирования производных из формул (5) перенумерацией Y1, Y2, Y3, Y4 на Y+0, Y+1, Y+2, Y–0 получаем
 (14) (14)
где
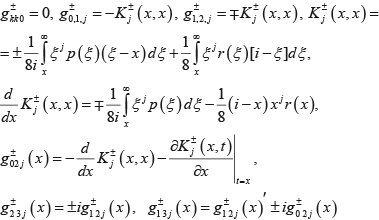
Используя оценки

из [11], подставляя (14) в (2), убеждаемся, что функции A(λ) и B(λ) соответственно являются регулярными функциями в верхней и нижней полуплоскостях, следовательно, нули этих функций образуют конечное или счетное множество.
Теорема 3. Операторный пучок Lαλ может иметь лишь конечное или счетное число собственных значений, образующих ограниченное множество в комплексной λ-плоскости с разрезом вдоль вещественной оси. Предельные точки этого множества могут находиться только на вещественной оси.
Доказательство. Теперь построим явный вид резольвенты R(±)αλ дифференциального пучка L(±)αλ в каждой полуплоскости İmλ>0 в отдельности.
Предположим, что область определения резольвенты R(±)αλ содержит функции f(x), равные нулю вне произвольного конечного интервала [0,a].
Положим, R+αλf=Y, т.е. LλY=f. Это означает, что Y(x,λ) есть решение уравнения
 (15) (15)
для любой функции f(x)∈L2(0,∞). Это решение принадлежит L2(0,∞) и удовлетворяет краевым условиям (2).
Имея фундаментальные системы решений Yi(x,λ), i=1,4 однородного дифференциального уравнения (1), методом вариации произвольных постоянных находим общее решение неоднородного дифференциального уравнения (15).
Общее решение ищем в виде
 (16) (16)
Согласно этому методу предположим, что C1, C2, C3, C4 являются функциями от x. Вычисляя все производные до четвертого порядка включительно, выражения (16) и подчиняя дополнительным условиям, получаем некоторую систему уравнений относительно Ci'(x), i=1,4.
Решая полученные системы, относительно Ci'(x) имеем
 (17) (17)
где
 (18) (18)
Здесь W(x,λ) – определитель Вронского от Y1(x,λ), Y1(x,λ), Y3(x,λ), Y4(x,λ), а Wi(x,λ) – алгебраическое дополнение элемента Y(3)i(x,λ) в вронскиане W(x,λ).
Из общей теории обыкновенных дифференциальных уравнений известно, что функции Z+i(x,λ), i=1,4 являются решениями уравнения l*(x,d/dx,λ)Z=0 транспонированного к уравнению (1).
Из (17) получаем
 (19) (19)
Подставляя (19) в (16), имеем
 (20) (20)
В открытой верхней полуплоскости Yi(x,λ)∈L2(0,∞), i=1,3, Y4(x,λ)∈L2(0,∞), Z+1(x,λ)∈L2(0,∞), Z+i(x,λ)∈L2(0,∞), i=2,4. Поэтому Y(x,λ)∈L2(0,∞) возможно лишь тогда, когда сумма коэффициентов при Y4(x,λ) равна нулю, т.е. когда

Подобное равенство можно также записать в виде

ибо f(x)=0 при x>a. С учетом этого выражение (20) имеет вид
 (21) (21)
Отсюда

Поскольку из определения функции Z+i(x,λ), i=1,4 следует, что

С помощью граничных условий имеем:

т.е.

Решая эту систему уравнений относительно Ci, i=1,3 получим что
 (22) (22)
где A(λ)=det||Uv(Yk)||3v,k=1≠0, Ai(λ) – определитель, полученный из A3(λ) заменой Uv(Yi) на Uv(Y4).
Обозначая через
 (23) (23)
можем записать:
 (24) (24)
Подставляя эти значения в (21) имеем:
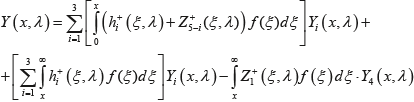
Обозначая через K+(x,ξ,λ) ядро резольвенты R+αλ в верхней полуплоскости
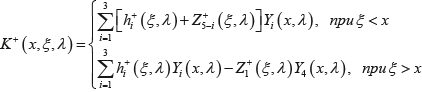 (25) (25)
и введя переобозначения Z+5–i(ξ,λ)=ω+i(ξ,λ), i=1,4, имеем
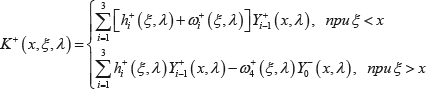 (26) (26)
где

Из последнего выражения можем написать:
 (27) (27)
Теперь рассмотрим открытую нижнюю полуплоскость. В этой полуплоскости Y–0(x,λ)∈L2(0,∞), Y+i(x,λ)∈L2(0,∞), i=1,3. А для решений сопряженного уравнения Z–i(x,λ)∈L2(0,∞), i=1,3; Z–4(x,λ)∈L2(0,∞). В этом случае, перенумеруя Y–0,Y+0, Y+1, Y+2 соответственно через Y1, Y2, Y3, Y4 имеем, что Y1(x,λ)∈L2(0,∞), Yi(x,λ)∈L2(0,∞), i=2,4. Тогда функция Y(x,λ) выраженная в виде
 (28) (28)
принадлежит L2(0,∞) тогда и только тогда, когда сумма коэффициентов функций Yi(x,λ), i=2,4 равна нулю, т.е.
 (29) (29)
где f(x)=0 при x≥a.
С учетом (29) выражение (28) имеет вид
 (30) (30)
Отсюда

Учитывая, что

для фиксированного граничного условия имеем

Отсюда

Обозначая
 (31) (31)
можем написать
 (32) (32)
Подставляя это значение в (30), получаем:
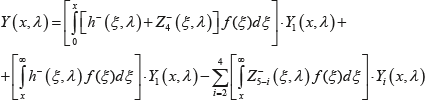 (33) (33)
Обозначая через K–(x,ξ,λ) выражение
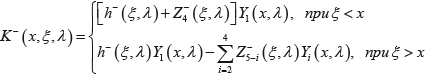 (34) (34)
и снова введя обозначения Z–5–i(ξ,λ)=ω–i(ξ,λ), i=1,4, получаем:
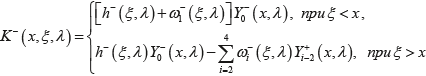 (35) (35)
где

Введенное обозначение удобно для записи ядра в компактном виде, и мы имеем следующее представление:
 (36) (36)
Теорема 4. Для всех значений спектрального параметра λ из открытой верхней и открытой нижней полуплоскостей, не являющихся корнями уравнения A(λ)=0 и B(λ)=0 резольвента оператора Lαλ определена на всем пространстве L2(0,∞), в нем является ограниченным интегральным оператором с ядрами типа Карлемана. При приближении λ к действительной оси норма резольвенты неограниченно возрастает, и вся действительная ось принадлежит непрерывному спектру пучка Lαλ.
Доказательство. В представлениях (25) и (34) ядра резольвенты, в верхней полуплоскости Yj(x,λ)∈L2(0,∞), j=1,3, Y4(x,λ)∈L2(0,∞), Z+1(x,λ)∈L2(0,∞), Z+j(x,λ)∈L2(0,∞), j=1,3, а в нижней полуплоскости Yj(x,λ)∈L2(0,∞), j=1,3, Y4(x,λ)∈L2(0,∞), Z–1(x,λ)∈L2(0,∞), Z–j(x,λ)∈L2(0,∞), j=1,3.
Учитывая, что xjξjeiλ(x–ξ), xjξje–iλ(x–ξ) являются доминантными членами в соответствующих выражениях, с привлечением неравенства

получается оценка

где

А это означает, что K(x,ξ,λ) является ограниченным интегральным оператором на всем пространстве L2(0,∞). Ввиду того, что ядро является ядром Гильберта-Шмидта, оно порождает вполне непрерывный оператор.
Оценки

типа Карлемана получаются из асимптотических разложений функций Yi(x,λ), Zi(x,λ), i=1,4 из представлений (25) и (34).
Теперь возьмем a>0, так что при x>a>0 выполнялось неравенство 0(1)<1/2.
Из оценки
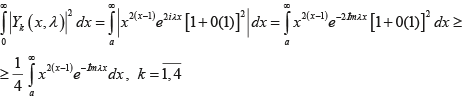
частично интегрируя правую часть, имеем следующую оценку:

где C±λ является многочленом третьей степени относительно 1/İmλ.
Из этой формулы вытекает, что при приближении λ к действительной оси норма резольвенты неограниченно растет.
Теперь покажем, что при λ∈(–∞;∞) область определения оператора Rαλ плотна в L2(0;∞), т.е. область значений Lαλ является плотной в L2(0;∞).
Предположим противное. Тогда в L2(0;∞), существует отличная от нуля функция f(x) что равенство (LαλY,f)=0 (т.е. (f,L*αλf)=0 ) должно выполняться для всех Y(x,λ)∈D(Lαλ). А это означает, что L*αλf=0, т.е. λ является собственным оператора (Lαλ)*. Но тогда λ стала бы собственным значением оператора Lαλ. Получили противоречие. Поэтому предположение f≠0 не имеет места.
Таким образом, вся действительная ось принадлежит непрерывному спектру оператора Lαλ. Если A(λ)=0, B(λ)=0 имеют действительные корни, тогда эти числа являются спектральными особенностями пучка Lαλ. Теорема доказана.
- Оруджев Э.Г. Прямые спектральные задачи для обыкновенного дифференциального уравнения четвертого порядка, полиноминально зависящего от спектрального параметра // Доклады АН Азербайджана, Т. LIV, № 1, 1998, стр. 9-15.
- Вагабов А.И. Квадратичные пучки обыкновенных дифференциальных операторов // Математические заметки, Т. 42, № 3, 1987, стр.381-393.
- Богомолова Е.П., Печенцов А.С. О базисных свойствах системы собственных функций краевой задачи с кратным корнем характеристического многочлена // Вестник Московского университета, сер. 1, математика, механика, 1989, № 4, стр.17-22.
- Гасымов М.Г., МагеррамовА.М. Исследование одного класса операторных пучков четного порядка // ДАН СССР, 1982, Т. 265, № 2, стр.277-280.
- Фунтаков В.Н. О разложении по собственным функциям несамосопряженно дифференциального пучка произвольного порядка на полуоси . I-II // I-II Известия АН Азерб. ССР, сер.физ-матем. и техн.наук, I:1960, № 6, стр.3-19; II:1961, № 1, стр.3-21.
- Максудов Ф.Г., Магеррамов А.М., Мамедов М.З. Спектральный анализ пучков дифференциальных операторов специального вида // ДАН СССР, 1990, Т.310, №1, стр.24-28.
- Оруджев Э.Г. Спектральный анализ дифференциальных операторов с кратными характеристиками на полуоси // Успехи математических наук, 1999, Т. 54, №2 (326), стр.181-182.
- Оруджев Э.Г. Резольвента и спектр одного класса несамосопряженных дифференциальных операторов с кратными характеристиками // Труды Института матем. и мех. АН Азербайджана, 1997, Т. VI(XII), стр.148-160.
- Мирзоев С.С., Оруджев Э.Г., Алиев А.Р. Спектральный анализ одного дифференциального пучка четвертого порядка на всей оси // Доклады РАН, 2012, Т. 442, № 3, стр.312-314.
- Sahil A.Aliyev On the existence of transformation operator for a fourth order differential equation with triple characteristics // Proceedings of IMM of NAS of Azerbaijan, 2013, vol. XXXIX, pp.3-8.
- Elshar G.Orudzhev and Sahil A.Aliyev Construction of a kernel of the transformation operator for a fourth order differential bundle with multiple charac-teristics // Proceedings of the Institute of Mathematics and Mechanics, National Academy of Sciences of Azerbaijan, vol. 40, Special Issue, 2014, pp.351-358.
Ключевые слова: спектр, собственная функция, резольвента, сопряженный оператор, ядро типа Карлемана.
Investigation of the spectrum and resolvent of a 4th order differential beam with a threefold characteristic root
Orujev E.G., Doctor of Physical and Mathematical Sciences, Professor, Head of the Department of Mathematical Economics, Baku State University, Republic of Azerbaijan, elsharorucov63@mail.ru
Aliev S.A., Nakhichevan Institute of Teachers, Department of Advanced Mathematics and Informatics, Senior Lecturer, Azerbaijan Republic, sahil.liyev83@mail.ru
Abstract: The article is considered that, the spectrum and the resolvent of a structure of fourth-order differential operators are investigated in space L2(0;∞), when one triple root is the main characteristic polynomial. It is shown that, a beam can have a finite or countable number of eigenvalues in theopen lower and open upper half-planes, and the continuous spectrum fills the entire real axis, where spectral features can be located. It is proved that, the resolvent of a structure is a bounded integral operator, defined on the whole space L2(0;∞), with a Carleman type.
Keywords: spectrum, eigen function, resolvent, ad joint operator, Carleman type.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
