 |
|
|
|
Генерируемая ASCII-графика в 1С
Генерируемая ASCII-графика в 1СРассматривается программа на языке 1С, позволяющая генерировать ASCII-изображение известного религиозного символа. Приводятся алгоритм, исходный код, результаты работы
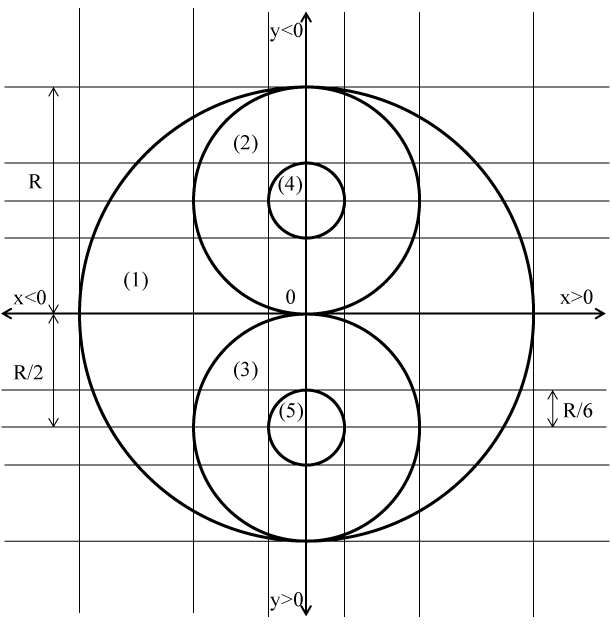
Одним из видов современного искусства является ASCII-графика [1]. В основном ASCII-графика играет вспомогательную, оформительскую, служебную роль. Несомненным ее преимуществом является возможность применения такой графики без наличия графических средств отображения информации. Например, построение изображений для сохранения их в текстовые файлы и вывода на печать. Для примера такого изображения можно выполнить текстовую генерацию религиозного символа, известного под названием Инь и Ян [2]. Генерация начнется с описания функциональных соотношений, которые ограничивают окружности, входящие в этот символ. Всего в символ входит пять окружностей, которые изображены на рис. 1.
Рисунок 1. Иллюстрация для формул Стоит отметить, что в отличие от общепринятой декартовой системы координат на рис. 1 и далее для удобства компьютерных расчетов предполагается, что условно верхняя полуось y содержит отрицательные величины (y < 0), в то же самое время нижняя – положительные (y > 0). Также в дальнейшем полагается, что рисунок генерируется на некотором двумерном текстовом поле, ячейки которого имеют целочисленные координаты (x, y). Согласно [3] уравнение окружности с центром в точке (x0,y0) и радиусом R имеет вид:
На основании (1), чтобы определить принадлежность точки окружности и кругу с центром в точке (x0,y0) и радиусом R необходима истинность выражения:
Наибольшая окружность получает номер 1, средние – 2 и 3, наименьшие – 4 и 5. Из рис. 1 следует, что для всех окружностей координаты x одинаковы:
С другой стороны, координаты y разнятся:
Очевидно, что радиусы окружностей равны, соответственно:
Удобно ввести формулу по (2) для определения принадлежности точки окружности и кругу с центром в точке (x0,y0) и радиусом R:
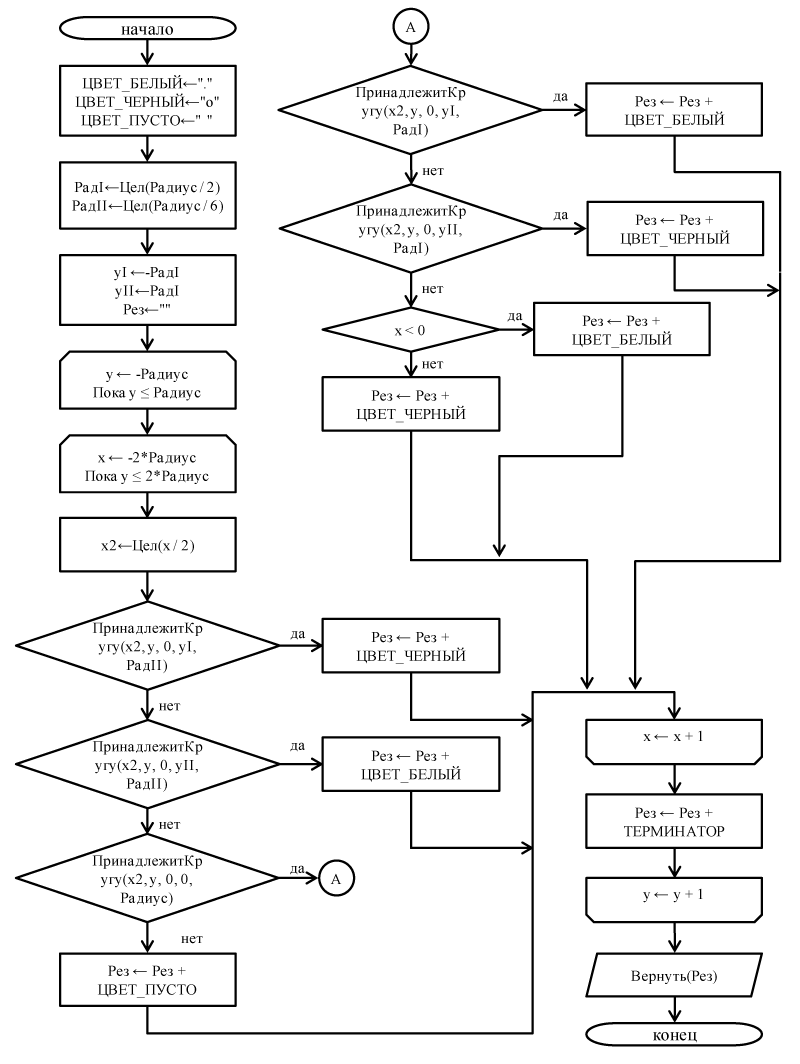
На основании (1)-(6) можно определить цвет ячейки двумерного текстового поля с координатами (x, y): Подставив в этот алгоритм значения (3)-(5), получаем: По этому алгоритму уже возможно формировать ячейки двумерного текстового поля и, соответственно, приступить к написанию программы, которая для выполнения расчетов будет располагаться в модуле управляемого приложения. Вначале определяется служебная функция, которая возвращает квадрат аргумента: Затем определяется функция, определяющая принадлежность точки с координатами (x, y) окружности и кругу с центром в точке (x0,y0) и радиусом Радиус: Расчет ведется по формулам (2), (6). Непосредственное построение ASCII-рисунка происходит в функции ИньЯн. Единственный аргумент этой функции – Радиус – это радиус большой окружности. Функция начинается с определения переменных: В переменных ЦВЕТ_БЕЛЫЙ, ЦВЕТ_ЧЕРНЫЙ, ЦВЕТ_ПУСТО сохраняются символы, которые будут в результирующей строке играть роль цветной точки. Переменные x и y – это счетчики циклов, указывающих координаты на поле рисунка. Для хранения результатов целочисленного деления величины радиуса на 2 и на 6 служат РадI и РадII. Центры средних и малых окружностей размещаются в yI и yII. Результат целочисленного уменьшения координаты x в два раза помещается в x2. Наконец, строка с ASCII-картинкой помещается в Рез. Устанавливаются символы, соответствующие цветам ячейки: Рассчитываются радиусы средних и малых окружностей: Определяются координаты y центров средних и малых окружностей: Результирующая выходная строка пуста: По всем координатам y, которые могут принадлежать большей окружности и кругу: По всем координатам y, которые могут принадлежать большей окружности и кругу, причем применяется масштабирование для учета распространенных соотношений сторон символов: Масштабирование отменяется: Если точка принадлежит малому верхнему кругу, то устанавливается черный цвет: Если точка принадлежит малому нижнему кругу, то устанавливается белый цвет: Если точка принадлежит большому кругу: И при этом принадлежит верхнему среднему кругу, то устанавливается белый цвет: И при этом принадлежит нижнему среднему кругу, то устанавливается черный цвет: Если же находится слева, то цвет нужно выставлять белый: Если находится справа, то цвет черный: Иначе к результирующей строке добавляется символ пустой ячейки: Внутренний цикл повторяется: К результирующей строке добавляется терминатор и повторяется внешний цикл: Результат возвращается и функция завершается: Пользователю сообщаются результаты расчетов ASCII-рисунков для радиусов 8 и 16: Схема соответствующего программе алгоритма приводится на рис. 2.
Рисунок 2. Схема алгоритма Полный текст программы доступен на сайте журнала http://samag.ru. Результаты работы – см. рис. 3.
Рисунок 3. Результаты работы программы Полученные алгоритм и программа позволят глубже взглянуть на простейшие, элементарные управляющие конструкции языка 1С. Многократное повторение и использование этих важных конструкций позволит закрепить знание основ языка 1С.
Ключевые слова: 1С, ASCII. |
КИРИЛЛ ТКАЧЕНКО, инженер 1-й кат., ФГАОУ ВО «Севастопольский государственный университет», 
Изучение алгоритмических языков программирования должно начинаться с наиболее простых примеров. В частности, необходимо уделить особое внимание базовым элементам языка, таким как операторы цикла и условные операторы. Безих знания во многих случаях невозможно будет правильно и полноценно программировать. Поэтому кажется разумным уделить особое внимание им. Необходимо совместить как рассмотрение указанных операторов, так и манипулирование графикой в текстовом режиме, для которой стоит продолжить рассмотрение.
(1)
(2)
(3)
(4)
(5)
(6)
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
