ШАРИКОВ Д.В., Московский авиационный институт (национальный исследовательский университет), 812-я кафедра, инженер

 ПОВАЛЯЕВ П.П., Московский авиационный институт (национальный исследовательский университет), 812-я кафедра, инженер

 ЕГОРОВА М.В., Московский авиационный институт (национальный исследовательский университет), 812-я кафедра, ведущий инженер

Оценка построения индивидуальной траектории обучения
английскому языку при помощи математических методов

В рамках данной статьи было спроектировано приложение на языке программирования С++. Создана программа, позволяющая успешно определить индивидуальную траекторию обучения для последующей подготовки к сдаче экзамена уровня FCE или выявить недостатки развития на данный момент. Пользователь может анализировать свои показатели, которые приведены как в виде результирующей матрицы, так и в виде диаграмм. Был проведен анализ разных типов экзаменов по английскому языку и разных математических аппаратов, которые нашли свое применение в модели для данной работы. Предложенная здесь модель является универсальной: ее можно применить не только для экзаменов типа FCE, но и даже в иных сферах (необязательно это может быть только английский язык). Это могут быть самые разные виды тестов по самым разным предметам: экзамены по математике, русскому языку, экономике, вузовским дисциплинам; экзамены типа ЕГЭ, ОГЭ, внутренние вузовские испытания и т.д., что говорит о необходимости продолжения применения данной модели под самый разный спектр задач

Обучение – целенаправленный педагогический процесс организации и стимулирования активной учебно-познавательной деятельности учащихся по овладению знаниями, умениями и навыками, развитию творческих способностей инравственных этических взглядов.

В рамках данной работы предлагается специальная программа, с помощью которой можно не только сверить свои навыки английского языка, но и выявить для каждого субъекта свою собственную траекторию обучения, то есть определить, является ли уровень навыков достаточным для успешной подготовки к прохождению экзамена по английскому языку типа FCE или требует направления для улучшения этих самых навыков. Это приложение будет полезным не только длястудентов и желающих сдать экзамен, но и для преподавателей: если они занимаются в группах, то с помощью этого приложения можно гораздо удобнее оформить учебный процесс: дать нужные советы и методические указания испытуемому.

Чтобы обосновать актуальность данной работы, необходимо принять к сведению следующее:

• актуальность с научной точки зрения. Возможность объединения двух столь, казалось бы, полярно противоположных по смыслу направлений, как гуманитарные и технические науки (в нашем случае это социально-педагогическая сторона обучения и техническая сторона математического моделирования стратегии обучения), всегда привлекала как ученых, так и обывателей. Данную работу можно назвать очередной попыткой этого самого объединения, так что, стеоретической точки зрения, актуальность видна. Как будет указано далее, данная модель является довольно универсальной, что говорит о необходимости поиска вариантов ее применения и в прочих сферах жизни.
• актуальность с практической точки зрения. Выбор оптимальной стратегии обучения человека – очень серьезный и трудный процесс: в детских садах имеется тенденция недостаточности формирования мышления, необходимого для комфортного дальнейшего развития ребенка; в школах далеко не каждый ученик получает исключительно отличные оценки и, в зависимости от ситуации, имеет разные сложности в понимании и усвоении получаемого материала: то ли это определенный склад ума, то ли это анатомические отклонения человека. Понятно и естественно, что в нынешнем, быстро развивающемся мире необходимо постоянное обновление получаемых знаний, и как раз для этого особую ценность и актуальность имеют приобретение и развитие умений самостоятельной учебной деятельности и способности выстраивать индивидуальные образовательные траектории. В рамках данной работы была создана программа на языке С++, с помощью которой можно легко выявить, в каком направлении следует развивать свои навыки испытуемому.

Для проведения успешной работы по созданию индивидуальной траектории обучения и получения соответствующих высоких результатов впоследствии необходимо достижение конкретных результатов:

• Личностных, как готовность и способность обучающихся к саморазвитию и личностному самоопределению, сформированность их мотивации к обучению и целенаправленной познавательной деятельности, системы значимых социальных и межличностных отношений, ценностно-смысловых установок, отражающих личностные и гражданские позиции в деятельности, правосознании, способность ставить цели и строить жизненные планы.
• Метапредметных, которые включают в себя освоенные обучающимися межпредметные понятия и универсальные учебные действия (регулятивные, познавательные, коммуникативные), способность их использования в познавательной и социальной практике, самостоятельность в планировании и осуществлении учебной деятельности и организации учебного сотрудничества с педагогами и сверстниками, способность к построению индивидуальной образовательной траектории, владение навыками учебно-исследовательской, проектной и социальной деятельности.
• Предметных, которые включают в себя освоенные обучающимися в ходе изучения учебного предмета умения, специфические для данной предметной области. Одной из основных целей обучения иностранному языку наряду сразвитием и воспитанием выступает формирование иноязычной коммуникативной компетенции во всем многообразии ее компонентов.

При формировании обучающимися индивидуальных образовательных траекторий хорошо помогают когнитивные стили, т.е. устойчивые индивидуальные особенности познавательных процессов: восприятие, запоминание информации, мышление и т.д.

Подопечным невольно создается личный стиль обучения: то ли это аудиал (который лучше воспринимает информацию в виде звука слухом), визуал (который лучше воспринимает информацию глазами) или кинестетик (которому полезнее совершить определенное действие для наилучшего результата).

Надо также понимать, что людей с единственным стилем обучения чрезвычайно мало, т.е. обучающиеся склонны обычно применять все три стиля восприятия информации, хотя преобладает обычно какой-либо один.

Личностно-ориентированный подход к обучению предполагает построение такой образовательной модели, которая была бы ориентирована на конкретного ученика с его индивидуальными способностями, особенностями восприятия, получения и овладения материалом, интересами и потребностями.

Именно поэтому выстраивание индивидуальных образовательных траекторий позволит в полном объеме учитывать индивидуальные способности и возможности каждого ученика и поможет достичь ему наиболее эффективных результатов.

Научившись выстраивать индивидуальные образовательные траектории в период обучения в школе или вузе, обучающийся сможет самостоятельно использовать данную способность на протяжении всей жизни.

Целью данной работы является выявление оптимальной стратегии обучения для конкретного субъекта (человека, студента, испытуемого и т.д.) на примере тестов FCE (на выявление уровня подготовки к изучению английского языка).

Разработанная в ЕС система уровней владения иностранным языком под названием CEFR (Common European Framework of Reference) предусматривает общеевропейские компетенции владения иностранным языком, из которой выделяются3 категория, имеющие по 2 уровня соответственно:

• A – основной уровень использования языка (basic)
  • А1) Начинающий (beginner)
  • А2) Элементарный (elementary)
• В – уровень уверенного использования языка (independent)
  • В1) Средний (intermediate)
  • В2) Выше среднего (upper intermediate)
• C – уровень умелого использования языка (proficient)
  • С1) Продвинутый (advanced)
  • С2) Профессиональный (mastery/proficient)

Имеется пять уровней экзаменов по английскому языку по Кембриджской системе (Cambridge ESOL examinations):

• KET (Key English Test) – экзамен, подтверждающий базовый уровень владения английским языком.
• PET (Preliminary English Test) – экзамен, подтверждающий средний уровень владения английским языком.
• FCE (First Certificate in English) – экзамен, подтверждающий высокий уровень владения английским языком.
• CAE (Certificate in Advanced English) – экзамен, подтверждающий уровень владения английским языком, достаточный для обучения/работы за границей.
• CPE (Certificate in Proficiency English) – экзамен, сдача которого подтверждает максимальный уровень владения английским языком.

Далее будет представлен математический аппарат, который будет использован для построения индивидуальной траектории обучения. Чтобы выявить общий уровень развития английского языка, достаточно взять среднее арифметическое изсуммы баллов, полученных за все задания. Для этого воспользуемся критериями Лапласа, Вальда, Гурвица и Сэвиджа, которые обычно используются при формировании стратегии в играх с природой.

Критерий Лапласа – наибольшее значение математического ожидания выигрыша в условиях неопределенности состояний природы, т.е. наибольшее среднее арифметическое значение выигрыша.

• m – число стратегий
• n – число состояний природы
• a_ij – выигрыш при i-ой стратегии при j-ом состоянии природы
• p_j – вероятность j-ого состояния природы
• L(X*) – критерий Лапласа

В рамках данной модели стратегиями будем называть направления деятельности по обучению (лексика, чтение и др.) и обозначать латинской буквой R с индексами 1, 2 и т.д., а состояниями будут являться порядковые номера заданий (1, 2 и т.д.), обозначим буквой S с соответствующими индексами.

Критерий Лапласа основан на гипотезе равновероятности и содержательно может быть сформулирован так: «поскольку мы ничего не знаем о состояниях среды, их надо считать равновероятными».

Пример: рассмотрим таблицу 1.

Таблица 1. Некоторая таблица значений, имеющая 3 задания по 2 направлениям

В данной таблице имеются некоторые значения в соответствии с двумя стратегиями (R) и тремя состояниями (S). Для выявления оценки по каждой из стратегий воспользуемся формулой выше и получим следующие значения:

Так как в нашей работе требуется определить те позиции, по которым на данном этапе выявлены недостатки, нас будут интересовать только L такие, что L → min, следовательно, искомая стратегия в данном примере R₂.

Критерий Вальда – это числовая характеристика стратегий в играх с природой, значением которой является наибольшее значение выигрыша, причем пессимистический критерий – это гарантированный выигрыш, а оптимистический критерий – это максимально возможный выигрыш.

Пессимистический критерий:

Оптимистический критерий:

• m – число стратегий;
• n – число состояний природы;
• a_ij – выигрыш при i-ой стратегии при j-ом состоянии природы;
• W(X*) – критерий Вальда.

Будем пользоваться пессимистическим критерием. Критерий Вальда основан на гипотезе крайней осторожности (крайнего пессимизма), которую можно сформулировать таким образом: «При выборе той или иной стратегии надо рассчитывать на худший из возможных вариантов».

Пример: воспользуемся данными из таблицы 1 для применения критерия Вальда, тогда получим следующие значения:

Аналогично решению задачи с помощью критерия Лапласа используем значение W такое, что W → min. Видим, что искомая стратегия также R₂.

Критерий Гурвица – это числовая характеристика стратегий в играх с природой, значением которой является наибольшее средневзвешенное значение выигрыша, причем доля пессимизма задается с помощью коэффициента.

• m – число стратегий
• n – число состояний природы
• a_ij – выигрыш при i-ой стратегии при j-ом состоянии природы
• λ – доля пессимизма, 0 ≤ λ ≤ 1
• 1–λ – доля оптимизма
• G(X*) – критерий Гурвица

Значение коэффициента λ весьма условное, но берется обычно λ = 0.8. В рамках данной модели будем придерживаться именно этого значения. Для удобства записи долю оптимизма (1 – λ) иногда обозначают буквой α. При λ = 1 критерий Гурвица становится критерием Вальда.

Пример: воспользуемся данными из таблицы 1 для применения критерия Гурвица. Тогда получим следующие значения:

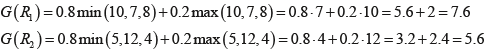
По смыслу задачи используем G такое, что G → min. Видим, что искомой стратегией и на сей раз является R₂, как и по предыдущим критериям.

Стоит отметить, что при разных значениях коэффициента критерий ведет себя по-разному.

Критерий Сэвиджа – это числовая характеристика стратегий в играх с природой, значением которой является наименьшее значение риска, т.е. гарантированное значение минимальных потерь.

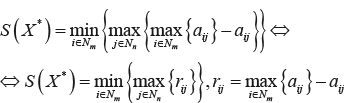
• m – число стратегий;
• n – число состояний природы;
• a_ij – выигрыш при i-ой стратегии при j-ом состоянии природы;
• r_ij – потери при выборе i-ой стратегии по сравнению с наибольшим выигрышем при j-ом состоянии природы;
• S(X*) – критерий Сэвиджа.

В отличие от предыдущих критериев оптимальная стратегия – та, что минимизирует значение S(X*), таким образом, нас будут интересовать максимальные значения. Этот критерий – мера сожаления о незнании истинного состояния среды.

Пример: воспользуемся в очередной раз данными из таблицы 1 для применения критерия Сэвиджа и получим следующие данные:

Сопоставим эти данные в новую таблицу 2.

Таблица 2. Таблица сожалений для наглядного представления сути критерия Сэвиджа

Значения по R₁ и R₂ в данном случае оказались идентичными, однако при решении других подобных задач используем S только такие, что S → min.

Как вы успели заметить, даже в рамках такого несложного примера может случиться так, что в зависимости от выбора критерия искомые стратегии могут отличаться: в рамках критериев Лапласа, Вальда и Гурвица искомой стратегией является строго R₂, однако, воспользовавшись критерием Сэвиджа, получаем, что развитие требуется также и в R₁. Тогда испытуемому будет рекомендовано развитие, прежде всего по R₂, однако R₁ тоже будет указано в рекомендациях вкачестве второстепенного пункта для улучшения навыков.

Нетрудно догадаться, что возможно получение таких решений, при которых мажоритарными будут являться сразу несколько стратегий. Тогда в зависимости от ситуации будут рекомендованы соответствующие пожелания.

Таблица 3. Некоторая таблица значений, имеющая 6 заданий по 6 направлениям

Пример: воспользовавшись данными из таблицы 3, выявим искомую стратегию R с помощью использованных ранее методов.

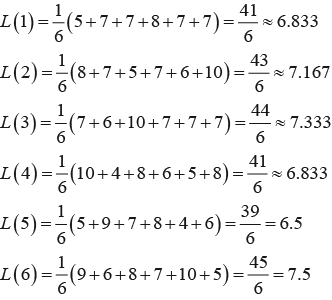
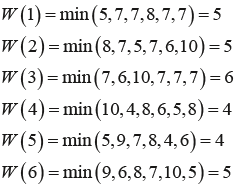
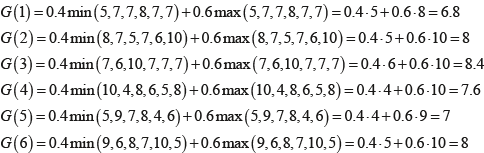
Таблица 4. Таблица сожалений, выражаемая из таблицы 3

Выполнив необходимые вычисления, получим, что по критерию Лапласа и Сэвиджа искомой стратегией является R₅, по критерию Вальда – R₄ и R₅, а по критерию Гурвица – R₁. Полученные результаты говорят о том, что улучшение требуется сразу по нескольким направлениям: R₁, R₄ и R₅.

Важное замечание. Воспользуемся данными из таблицы 3 и высчитаем средний балл за прохождение теста:

А теперь высчитаем среднее арифметическое значений по критерию Лапласа:

Можно сделать вывод, что средний балл за весь тест можно рассчитывать двумя способами: либо взять среднее арифметическое по всем элементам матрицы, либо взять среднее арифметическое значений всех критериев Лапласа. Это утверждение справедливо, потому что критерий Лапласа, по сути, высчитывает среднее арифметическое по строке (одной стратегии), а общее количество используемых элементов одинаково как для вычисления одним, так и другим способом.

Докажем это утверждение. Рассмотрим общий вид получаемой матрицы:

тогда

Среднее арифметическое элементов выглядит следующим образом:

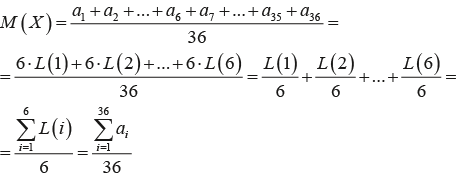
Следовательно, утверждение действительно справедливо: общий средний балл за тест можно считать как средним арифметическим всех объектов, так и средним арифметических полученных значений критериев Лапласа. Следует обратить внимание на разницу между получением одной или нескольких искомых стратегий. Если ответом являются несколько R, это необязательно говорит о том, что общий уровень навыка английского языка низкий, просто соответствующее улучшение в таком случае следует провести сразу по нескольким направлениям.

В рамках данной работы приложение, написанное на языке С++, на основе полученных на вопросы ответов строит матрицу 6х6 (6 направлений по 6 заданий на каждое). Значениями в этой матрице являются целые числа от 1 до 10, причем при правильном ответе на вопросы в матрицу заносятся значения от 8 до 10, а в случае неверного ответа – от 1 до 7 соответственно. Оценка зависит также от длительности и качества выполнения задания. На основе этой матрицы можно выявить:

• средний балл испытуемого
• значения критериев по каждому из направлений
• направление, по которому следует дальше развиваться

Учитывая, что максимальный балл за правильное решение задания равен 10, а минимальный 8, то в рамках данной модели можно считать значение среднего балла выше 8.5 очень хорошим результатом прохождения теста, выше 7 – хорошим, выше 5.5 – приемлемым. Если средний балл участника теста оказался меньше 5.5, необходимо всеобъемлющее развитие навыков (особенно по стратегиям, которые будут указаны в соответствующих критериях).

Пример: произвести анализ следующих результатов теста.

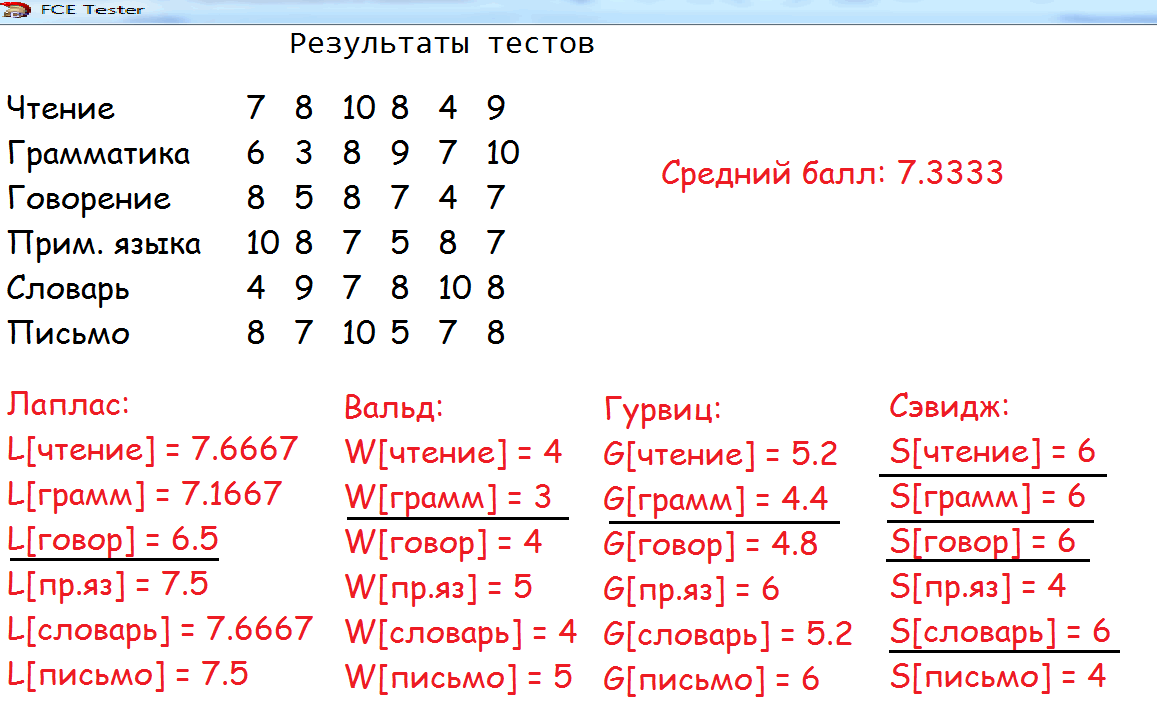
На рис. 1 указан экран приложения, на котором изображены результаты прохождения тестов в соответствии со стратегиями. Черным цветом подчеркнуты искомые стратегии по каждому из критериев: например, по Лапласу требуется развитие в стратегии «Говорение», а по Сэвиджу – сразу по 4 направлениям. «Грамматика» получила худшие результаты по 3 из 4 критериев. Это означает, что именно «Грамматика» требует максимальной проработки для участника теста.

Рисунок 1. Описание результатов теста

В рамках данной дипломной работы было спроектировано приложение на базе языка программирования С++, который представляет собой тестер экзамена по английскому языку типа FCE. Главный экран предлагает на выбор начать тест сразу, увидеть автора работы, получить справку о данной программе или закрыть приложение.

Рисунок 2. Главный экран приложения

При нажатии кнопки «Начать тест» появляется первый вопрос (по теме «Чтение»), и так поочередно появляются остальные из шести вопросов при выборе ответов и нажатии кнопки «Принять ответы и перейти к следующему вопросу».

После того как участник теста дал ответы на все вопросы, появится окно результатов.

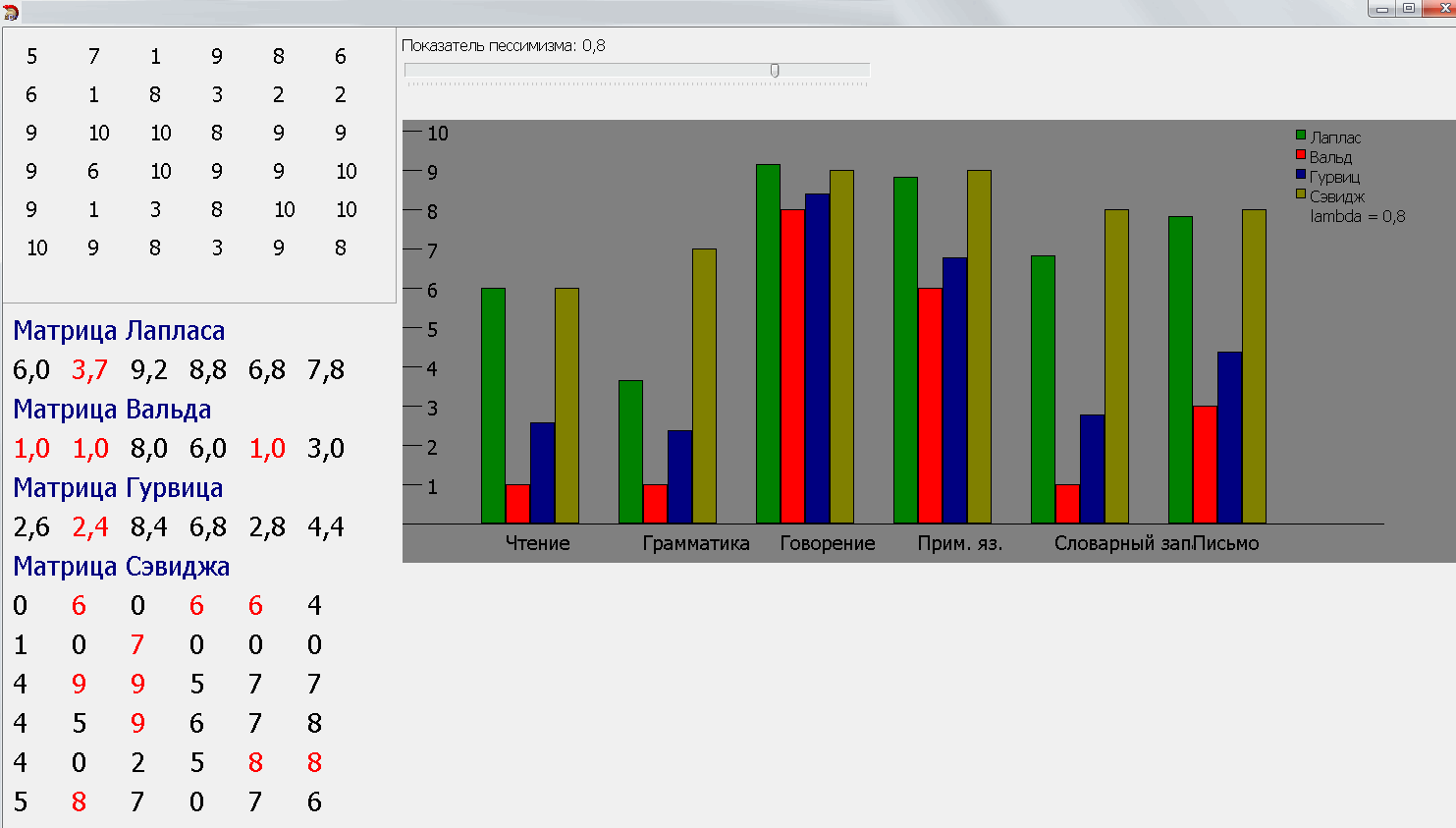
Рисунок 3. Показ результатов теста

Экран результатов теста наглядно демонстрирует полученную матрицу элементов в соответствии с правильностью выполнения заданий, численные значения применяемых критериев, а также наглядно демонстрирует индивидуальную траекторию с помощью диаграммы. По данным можно сделать вывод, что самую большую работу по улучшению навыков следует провести по стратегии R₂ (в нашей модели это грамматика), однако, обратив внимание на значения покритерию Гурвица, полезно развить также R₁ и R₅ (подтянуть чтение и словарный запас соответственно).

Можно также увидеть изменения значений критерия Гурвица с помощью полоски выбора «Показателя пессимизма», а также сохранять отдельно изображения диаграмм. Для этого необходимо щелкнуть мышью по диаграмме и сохранить изображение в формате *.png.

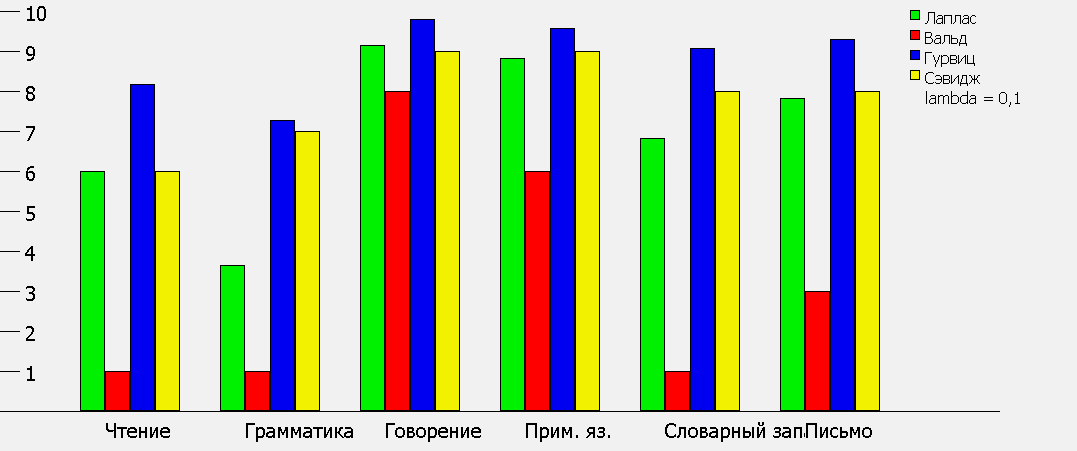
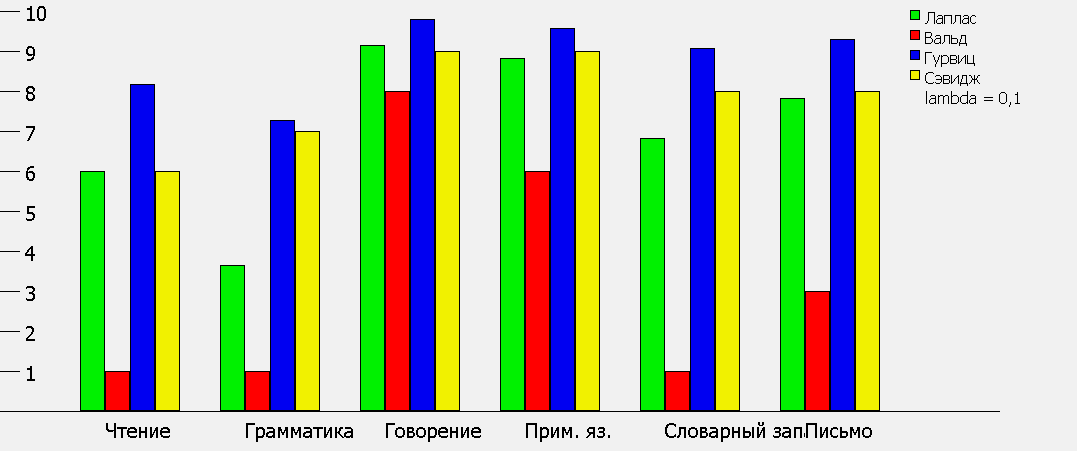
Рисунок 4. Диаграмма, описывающая результат теста при lambda = 0.1

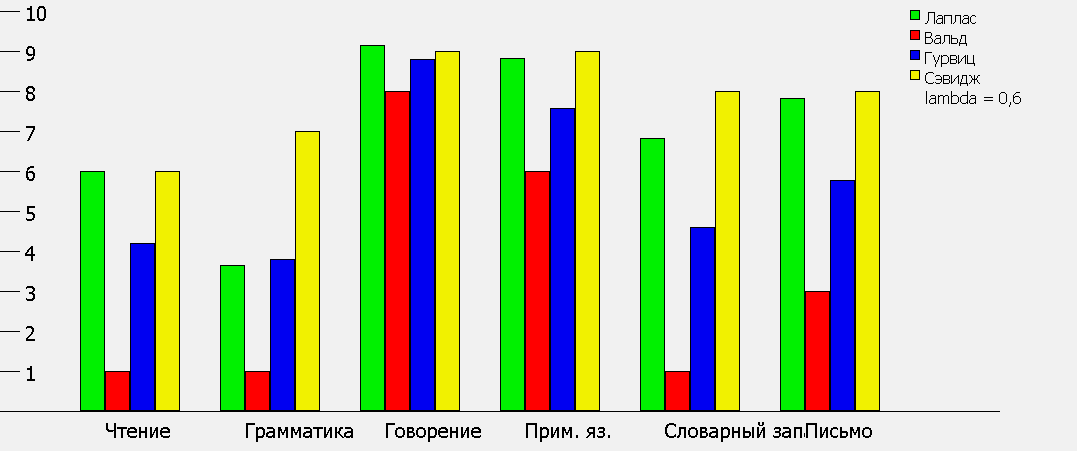
Рисунок 5. Диаграмма, описывающая результат теста при lambda = 0.6

Рисунок 6. Диаграмма, описывающая результат теста при lambda = 0.95

Как можно заметить, значения критерия Гурвица в данной программе выделены синим цветом. При разных значениях доли пессимизма lambda можно наблюдать, каким образом изменяются значения критериев: чем ближе значение lambda кединице, тем ближе значение критерия Гурвица к критерию Вальда, о чем говорилось выше.

Говоря о данном приложении, можно его улучшить путем увеличения базы данных тестовых вопросов и постепенного приведения программы в вид, наиболее близкий к реальному по экзамену FCE. В процессе решения разного рода задач были выявлены полезные закономерности при подсчете среднего балла за весь тест, а также выявления зависимости значения критерия Гурвица от доли пессимизма λ.

Рассмотрим небольшие кусочки кода программы. Файл с описанием стартового окна:

#include 
#pragma hdrstop
#include "Unit1.h"
#include "Unit2.h"
#include "Unit3.h"
#pragma package(smart_init)
#pragma resource "*.dfm"
TStartForm *StartForm;

void __fastcall TStartForm::ExitButtonClick(TObject *Sender)
{
	Close();
}

void __fastcall TStartForm::AuthorButtonClick(TObject *Sender)
{
	AuthorForm->ShowModal();
}

void __fastcall TStartForm::StartButtonClick(TObject *Sender)
{
	TestForm->ShowModal();
}

void __fastcall TStartForm::HelpButtonClick(TObject *Sender)
{
	ShowMessage (“Приложение представляет собой 
	тренажер для прохождения экзаменов типа FCE.
	\nПользователю следует пройти задания в следующем 
	порядке: Чтение (Reading), Грамматика (Grammar), 
	Устная речь (Speaking), Применение языка (Use 
	of English), Лексика (Vocabulary), Письмо (Writing).
	\nПо результатам выполнения заданий будет 
	сформирована таблица, по значениям элементов которой 
	строится индивидуальная траектория обучения.\nПо ней 
	можно наглядно выявить, в каком направлении следует 
	развивать навыки испытуемому.”);
}

Файл с описанием окна прохождения заданий:

#include 
#pragma hdrstop
#include "Unit1.h"
#include "Unit2.h"
#include "Unit3.h"
#include "Unit4.h"
#pragma package(smart_init)
#pragma resource "*.dfm"
TTestForm *TestForm;
int nOffset = 0, nBlockIdx = 0;
int Correct[] = {0,1,3,1,1,3, 2,1,2,0,2,2, 3,0,1,1,3,2, 3,0,1,0,2,3, 3,1,0,3,2,1, 1,0,2,2,2,1} ;
extern int A[36];

void __fastcall TTestForm::ExitButtonClick(TObject *Sender)
{
	Close();
}

void __fastcall TTestForm::TestButtonClick(TObject *Sender)
{
	TestButton -> Visible = false;
	QuestLabel -> Caption = ("Read the text carefully, and for questions 1-6, choose the answer which you think fits best, according to the text. ");
	Image1 -> Picture ->LoadFromFile("task1.jpg");
	Label1 -> Visible = true;
	RadioGroup1 ->Visible = true;
	Label2 -> Visible = true;
	RadioGroup2->Visible = true;
	Label3 -> Visible = true;
	RadioGroup3 ->Visible = true;
	Label4 -> Visible = true;
	RadioGroup4 ->Visible = true;
	Label5 -> Visible = true;
	RadioGroup5 ->Visible = true;
	Label6 -> Visible = true;
	RadioGroup6 ->Visible = true;
}
int rangeValue(int nFrom, int nTo)
{
   return nFrom+random(nTo-nFrom+1);
}

void doRadioButton (TRadioGroup *nItem, TLabel *nLabelItem, int lOffset)
{
 bool isCorrect = false;
 int nQuestionIdx = (int)lOffset*0.25;
 isCorrect =  (nItem->ItemIndex == Correct[nQuestionIdx]);
 A[nQuestionIdx] = (isCorrect?rangeValue(8,10):rangeValue(1,7));
nItem->Items->Clear();
  for (int i = lOffset; i < lOffset + 4; i++) {
	  nItem->Items->Add(TestForm->Memo1->Lines->Strings[i]);
 }
  nLabelItem->Caption = TestForm->Memo2->Lines->Strings[nQuestionIdx]; //номер вопроса
}

void __fastcall TTestForm::Button1Click(TObject *Sender)
{
 Button1->Enabled = false;
 TestForm->QuestLabel->Caption = TestForm->Memo3->Lines->Strings[nBlockIdx];
 doRadioButton(RadioGroup1, Label1, nOffset); nOffset+=4;
 doRadioButton(RadioGroup2, Label2, nOffset); nOffset+=4;
 doRadioButton(RadioGroup3, Label3, nOffset); nOffset+=4;
 doRadioButton(RadioGroup4, Label4, nOffset); nOffset+=4;
 doRadioButton(RadioGroup5, Label5, nOffset); nOffset+=4;
 doRadioButton(RadioGroup6, Label6, nOffset); nOffset+=4;
 nBlockIdx++
 if (nBlockIdx == 6)
 {
  Form4->ShowModal();
 }}
void __fastcall TTestForm::RadioGroup1Click(TObject *Sender)
{
 Button1->Enabled = (RadioGroup1 ->ItemIndex != -1) && (RadioGroup2 ->ItemIndex != -1) && (RadioGroup3 ->ItemIndex != -1) && (RadioGroup4 ->ItemIndex != -1) && (RadioGroup5 ->ItemIndex != -1) && (RadioGroup6 ->ItemIndex != -1);
}
void __fastcall TTestForm::Button2Click(TObject *Sender)
{
 Form4->ShowModal();
}

1. Paul A. Davies & Tim Falla – Revised FCE Result: Student’s Book.
2. http://cyclowiki.org/wiki/Критерий_Лапласа.
3. http://cyclowiki.org/wiki/Критерий_Сэвиджа.
4. http://cyclowiki.org/wiki/Критерий_Вальда.
5. http://cyclowiki.org/wiki/Критерий_Гурвица.
6. Сысоев П.В. Обучение по индивидуальной траектории.

Ключевые слова: индивидуальная траектория обучения, FCE, язык С++, когнитивный стиль, личностно-ориентированный подход, CEFR, критерий Лапласа, критерий Вальда, критерий Гурвица, критерий Сэвиджа.

Evaluation of the construction of an individual trajectory teaching English with mathematical methods

Sharikov D.V., Moscow Aviation Institute (National Research University), 812 department, engineer

Povalyaev P.P., Moscow Aviation Institute (National Research University), 812 department, engineer

Egorova M.V., Moscow Aviation Institute (National Research University), 812-th Department, Lead Engineer

Abstract: In the framework of this article, an application in the programming language C ++ was designed. A program has been created that allows to successfully determine the individual trajectory of training for the subsequent preparation for the FCE level examination or to identify the development shortcomings at the moment. The user can analyze his indicators, which are given both in the form of the resulting matrix, and in the form of diagrams. An analysis was made of different types of exams in English and various mathematical devices, which found their application in the model for this work. The model proposed here is universal: it can be applied not only for exams of the FCE type, but also in other spheres (it can not be English only). It can be avariety of types of tests in a variety of subjects: examinations in mathematics, the Russian language, economics, university disciplines; exams such as the Unified State Examination, OGE, internal high school tests, etc., which indicates the need to continue to use this model for a wide range of tasks.

Keywords: individual trajectory of learning, FCE, C ++ language, cognitive style, personality-oriented approach, CEFR, Laplace criterion, Wald criterion, Hurwitz criterion, Savage criterion.

Комментарии могут оставлять только зарегистрированные пользователи