|
Рубрика:
Наука и технологии
|
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
 ТРОЕНКО С.Ю., Московский авиационный институт (национальный исследовательский университет), бакалавр, 813-я кафедра ТРОЕНКО С.Ю., Московский авиационный институт (национальный исследовательский университет), бакалавр, 813-я кафедра
 ПОВАЛЯЕВ П.П., Московский авиационный институт (национальный исследовательский университет), 812-я кафедра, инженер ПОВАЛЯЕВ П.П., Московский авиационный институт (национальный исследовательский университет), 812-я кафедра, инженер
Разработка методов демпфирования колебаний
с помощью точечных стационарных демпферов. Часть 2. Колебания плоской мембраны
В данной статье рассматривается задача гашения колебаний плоской мембраны с использованием нескольких точечных демпферов. Предложены методы гашения колебаний плоской мембраны с использованием нескольких точечных стационарных демпферов для произвольных начальных возмущений. В качестве краевых условий рассмотрены условия закрепления. Разработан численный алгоритм решения задачи гашения колебаний плоской мембраны сиспользованием координатного метода. Разработано программное приложение, реализующее численные методы и визуализирующие основные результаты данной работы при различных значениях начальных данных. Приложение написано на языке С#
Задачи гашения колебаний актуальны в силу многочисленных технических приложений. Например, случай с двухкилометровым мостом в Волгограде, на котором 20 мая 2010 года по неизвестным причинам возникли колебания амплитудой до 1 метра, угрожавшие разрушением моста и остановившие движение транспорта.
Основной целью является разработка методов демпфирования колебаний тонкой мембраны с помощью нескольких точечных стационарных демпферов. В качестве граничных условий для мембраны рассматривается случай, когда оба конца мембраны закреплены. Также целью данной статьи является выбор наилучшего численного метода, позволяющего найти оптимальное управление, сводящее энергию колеблющейся мембраны к нулю за конечное время T. При этом необходимым является нахождение оптимальных параметров сходимости численного метода решения.
Колебания плоской мембраны
Колебания плоской мембраны описываются гиперболическим уравнением:
 (1.1) (1.1)
с начальными условиями:
 (1.2) (1.2)
которые будем считать начальными возмущениями и граничными условиями (условиями закрепления):
 (1.3) (1.3)
Энергия колебаний мембраны в момент времени t выражается следующим интегралом:
 (1.4) (1.4)
Поставим задачу гашения колебаний мембраны следующим образом: необходимо найти функцию g(t, x, y) из класса L2(0 ≤ t ≤ T, 0 ≤ x ≤ l1, 0 ≤ y ≤ l2), позволяющую перевести мембрану из состояния (1.2) в состояние покоя:
 (1.5) (1.5)
за минимальное время T > 0. Заметим, что условие (1.5) равносильно обращению интеграла энергии мембраны в ноль в момент времени T с учетом условий (1.3):
 (1.6) (1.6)
Основная идея заключается в использовании нескольких точечных демпферов. Будем искать функцию g(t, x, y) в виде:
 (1.7) (1.7)
где Wi – управляющие функции, δ – дельта-функция Дирака, xi, yj – точки, в которые помещаются демпферы.
Потребуем также, чтобы функции Wi(t) были ограничены некоторым значением Wmax:
 (1.8) (1.8)
Рассмотрим численный метод решения задачи гашения колебаний.
Численный алгоритм решения начально-краевой задачи для волнового уравнения
Для численного решения дифференциального уравнения (1.1) применяется метод сеток или разностный метод.
Рассмотрим задачу о приближенном вычислении производных функции u(x, y, t), определенной и имеющей непрерывные вторые частные производные uxx, uyy на отрезке x ∈ [0; l1], y ∈ [0; l2] и utt на отрезке [0; T].
Зададим натуральные числа M1, M2 и N, разобьем рассматриваемые отрезки {0 ≤ x ≤ l1, 0 ≤ y ≤ l2, 0 ≤ t ≤ T} на промежутки точками xm, yk и tn соответственно:
 (2.2) (2.2)
где hx = l1/M1, hy = l2/M2 и τ = T/N – шаги сетки по переменным x, y и t соответственно. В качестве сетки  используем совокупность точек пересечения плоскостей используем совокупность точек пересечения плоскостей  . Искомой сеточной функцией является таблица . Искомой сеточной функцией является таблица  значений. значений.
Обозначим:
ukm = 0(xk, ym, t) (2.3)
un = u(x, y, tn) (2.4)
Вторую производную uxx можно приближенно заменить второй разностной производной в точке  : :
 (2.5) (2.5)
Аналогичный вид примет вторая производная uyy:
 (2.6) (2.6)
Аппроксимация второй частной производной utt осуществляется аналогично и также имеет второй порядок:
 (2.7) (2.7)
Введем вместо точного решения u(xk, ym, tn) сеточную функцию  , которая будет удовлетворять следующему конечно-разностному соотношению: , которая будет удовлетворять следующему конечно-разностному соотношению:
 (2.9) (2.9)
Данное соотношение аппроксимирует уравнение (1.1) со вторым порядком по hx, hy и τ.
Выразим  : :

Аппроксимируем начальные условия (1.2). Первое начальное условие запишется в виде:

Для того чтобы аппроксимировать второе начальное условие (1.2), введем фиктивный слой t = -τ. Будем полагать, что уравнение (1.1) справедливо на промежутке [-τ; 0]. Решение на этом слое обозначим  . Аппроксимируем начальные условия со вторым порядком аппроксимации и выпишем разностную схему на слое n = 0: . Аппроксимируем начальные условия со вторым порядком аппроксимации и выпишем разностную схему на слое n = 0:
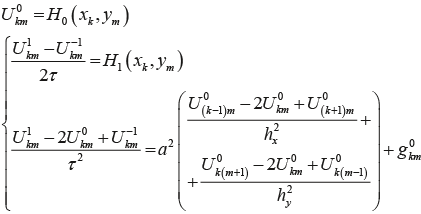
-110-115-web-resources/image/Eqn022.png) Выразим из первого уравнения Выразим из первого уравнения  и подставим во второе уравнение: и подставим во второе уравнение:

Получим выражение для  : :
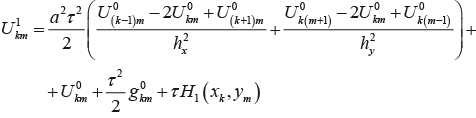
Краевые условия имеют вид:
 (2.10) (2.10)
В результате конечно-разностная аппроксимация уравнения (1.1) и начальных условий (1.2) имеет второй порядок аппроксимации.
Покажем, что составленная разностная схема (2.9) устойчива по Нейману. Будем искать решение (2.9) в виде:

Условие устойчивости по Нейману имеет вид |λ(p)|≤1 для всех p,q∈R. Тогда разностная схема будет иметь вид:
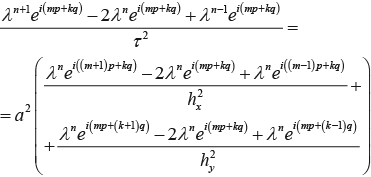 -110-115-web-resources/image/Eqn028.png) (2.11) (2.11)
После простейших математических преобразований получим следующее выражение:

Применяя формулу Эйлера:

получим квадратное уравнение следующего вида:

или
 (2.12) (2.12)
Если

то уравнение имеет различные вещественные корни λ1 ≠ λ2, поэтому модуль одного из корней будет больше 1. Этот случай нас не устраивает.
Если
 (2.13) (2.13)
то корни уравнения будут комплексно-сопряженными, причем |λ1| = |λ2| = 1.
Запишем неравенство (2.13) в виде:

Правое неравенство выполняется при любых p, q. Из левого неравенства следует:
 (2.14) (2.14)
Следовательно,
 (2.15) (2.15)
 (2.16) (2.16)
а значит, схема устойчива, если шаг по времени удовлетворяет неравенству (2.16).
Численный алгоритм выбора оптимального управления
Для численного расчета интеграла энергии мембраны воспользуемся следующей аппроксимацией:
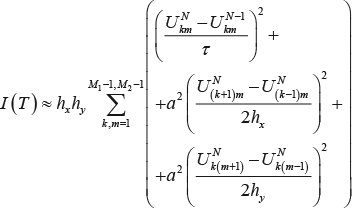 -110-115-web-resources/image/Eqn039.png) (2.17) (2.17)
Условием гашения будем полагать выполнение неравенства I(T) ≤ ε, где ε – заданная точность вычислений.
Аппроксимируем управляющие функции Wi(t) кусочно-постоянными функциями, такими что ∀t ∈ [tn, tn+1]
 (2.18) (2.18)
Тогда интеграл энергии (2.17) будет являться функцией переменных  : :
 (2.19) (2.19)
Оптимальные значения  , минимизирующие интеграл энергии с заданной точностью ε и являющиеся искомым решением задачи, будем искать методом координатного спуска. Алгоритм метода координатного спуска для функции многих переменных Ф(x1, x2, …, xm) заключается в следующем: , минимизирующие интеграл энергии с заданной точностью ε и являющиеся искомым решением задачи, будем искать методом координатного спуска. Алгоритм метода координатного спуска для функции многих переменных Ф(x1, x2, …, xm) заключается в следующем:
- Задаем начальные приближения
 . .
- Рассматриваем функцию
 . Она является функцией одной переменной x1. Будем искать локальный минимум этой функции методом парабол. . Она является функцией одной переменной x1. Будем искать локальный минимум этой функции методом парабол.
Описание метода. Метод квадратичной параболы, суть которого состоит в следующем: задается шаг h и вблизи выбранной точки x0 берутся точки x0-h, x0+h. Вычисляются значения функции f(x0), f(x0-h), f(x0+h) в этих точках. Через этиточки проводится квадратичная парабола:
 (2.21) (2.21)
 (2.22) (2.22)
 (2.23) (2.23)
Окончательно выражения для коэффициентов параболы выглядят следующим образом:
 (2.24) (2.24)
 (2.25) (2.25)
Если a > 0, то имеет место соотношение P2(x1) = 2a(x1 – x0) + b = 0, поэтому x1 = x0 – b/2a, где x1 является точкой минимума параболы. Далее вычисляем значения f(x1-h), f(x1), f(x1+h) и проводим новую параболу, то есть повторно вычисляем коэффициенты a, b, получаем x2 = x1 – b/2a. В случае если a < 0, находим минимальное среди полученных значений функций на предыдущем этапе: f(x0-h), f(x0), f(x0+h) и значению xi присваиваем соответствующее значение аргумента.
В результате применения метода парабол к функции f1(x1) находим  такую, что такую, что  . .
Далее рассматриваем функцию  . Эта функция является функцией одной переменной x2. Применяя метод парабол, находим . Эта функция является функцией одной переменной x2. Применяя метод парабол, находим  такую, что такую, что  . .
Далее повторяем эту процедуру для остальных переменных x3,…,xm. В результате мы получим следующее приближение  . .
Затем повторяем процесс 2 до тех пор, пока  . Затем уменьшаем переменную h в два раза и опять повторяем пункт 2. Процесс останавливаем, когда . Затем уменьшаем переменную h в два раза и опять повторяем пункт 2. Процесс останавливаем, когда  . .
Метод координатного спуска нахождения локального минимума функции многих переменных заключается в многократном применении метода парабол для различных искомых переменных. Метод сходится очень быстро и является одним из наилучших методов спуска.
Опишем программное приложение. Приложение реализовано средствами объектно-ориентированного языка C#. Основной функцией программы является расчет оптимального управления для задачи гашения колебаний мембраны. Вкачестве входных параметров программа использует размеры сетки M1, M2 и N. В качестве выходных параметров представлены файлы формата .txt, содержащие оптимальные значения.
Программа реализует следующие функции:
- прямой расчет – получение значений функции U;
- вычисление интеграла энергии колебаний мембраны;
- минимизация интеграла энергии колебаний методом координатного спуска.
Приложение не имеет значительных функциональных ограничений, однако предназначена для использования лишь на некоторых операционных системах семейства Windows и не подходит для реализации на операционных системах семейства Unix.
Алгоритм программной реализации выглядит следующим образом:
- Проводим прямой расчет значений функции U.
- Вычисляем значение интеграла энергии колебаний мембраны.
- Проводим расчеты коэффициентов метода парабол по формулам (2.23) – (2.25).
- Вычисляем оптимальные значения.
- Сравниваем значение полученного нового интеграла энергии с его старым значением по абсолютной величине. Если значение нового интеграла меньше старого значения, запоминаем полученные значения
 и проводим расчеты снова. и проводим расчеты снова.
Прямой расчет значений функции U осуществляется функцией GetU(). Для программной реализации сеточная функция  интерпретируется как трехмерный массив U[k, m, n], поэтому заполнение ее значений осуществляется за счет цикла for(). Начальные условия, которые воспринимаются в качестве начальных возмущений колебаний мембраны, заданы в функциях GetH0() и GetH1(). Программный код функции GetU() представлен в листинге 1. интерпретируется как трехмерный массив U[k, m, n], поэтому заполнение ее значений осуществляется за счет цикла for(). Начальные условия, которые воспринимаются в качестве начальных возмущений колебаний мембраны, заданы в функциях GetH0() и GetH1(). Программный код функции GetU() представлен в листинге 1.
Листинг 1. Прямой расчет в функции GetU()
for (int n = 0; n <= N; n++)
for (int k = 0; k <= M1; k++)
for (int m = 0; m <= M2; m++) {
if (k == 10 && m == 10) G[k, m, n] = W1[n] + h;
else G[k, m, n] = 0; }
for (int n = 0; n <= N; n++)
for (int m = 0; m <= M2; m++) {
U[0, m, n] = 0;
U[M1, m, n] = Math.Sin(l1) * Math.Sinh(m * hy); }
for (int n = 0; n <= N; n++)
for (int k = 0; k <= M1; k++) {
U[k, 0, n] = 0;
U[k, M2, n] = Math.Sin(k * hx) * Math.Sinh(l2); }
for (int k = 1; k <= M1 - 1; k++)
for (int m = 1; m <= M2 - 1; m++)
U[k, m, 0] = GetH0(k * hx, m * hy);
for (int k = 1; k <= M1 - 1; k++)
for (int m = 1; m <= M2 - 1; m++)
U[k, m, 1] = a * a * tau * tau / (2.0 * hx * hx) * (U[k - 1, m, 0] - 2 * U[k, m, 0] + U[k + 1, m, 0]) + a * a * tau * tau / (2.0 * hy * hy) * (U[k, m - 1, 0] - 2 * U[k, m, 0] + U[k, m + 1, 0]) + U[k, m, 0] + tau * GetH1(k * hx, m * hy);
for (int n = 1; n <= N - 1; n++)
for (int k = 1; k <= M1 - 1; k++)
for (int m = 1; m <= M2 - 1; m++)
U[k, m, n + 1] = a * a * tau * tau / (hx * hx) * (U[k - 1, m, n] - 2 * U[k, m, n] + U[k + 1, m, n]) + a * a * tau * tau / (hy * hy) * (U[k, m - 1, n] - 2 * U[k, m, n] + U[k, m + 1, n]) + tau * tau * G[k, m, n] + 2 * U[k, m, n] - U[k, m, n - 1];
for (int k = 1; k <= M1 - 1; k++)
for (int m = 1; m <= M2 - 1; m++)
E += ((U[k, m, N] - U[k, m, N - 1]) / tau) * ((U[k, m, N] - U[k, m, N - 1]) / tau) + U[k, m, N] * U[k, m, N]; E *= hx * hy;
Console.WriteLine("E = " + E);
return E;
}
Код функции, вычисляющей минимум интеграла и предназначенной для поиска значений оптимального управления, представлен в листинге 2.
Листинг 2. Код функции Minimize()
if (Math.Abs(W1_old - w1[n]) < 0.0001) {
Console.WriteLine("W1_old = " + W1_old + " , w1[n] = " + w1[n]);
while (h > 0.0001) {
Minimize(w1, n);
};
result[n] = w1[n];
h = 0.1;
return; }
}
W1_old = w1[n];
E2 = func(ref U, 0, w1);
E1 = func(ref U, -h, w1);
E3 = func(ref U, h, w1);
a = (E1 - 2 * E2 + E3) / (2.0 * h * h);
if (a > 0) {
b = (E3 - E1) / (2.0 * h);
w1[n] = W1_old - b / (2.0 * a);
Minimize(w1, n);
}
else {
if (min(E1, E2, E3) == E1)
w1[n] = W1_old - h;
else if (min(E1, E2, E3) == E2)
w1[n] = W1_old;
else
w1[n] = W1_old + h;
Minimize(w1, n);
}
Оптимальные значения  интерпретируются как одномерные массивы W1[n], W2[n], … Для каждого из них существует массив копий W1_old[n], W2_old[n], …, в котором хранятся оптимальные значения, полученные на предыдущем шаге алгоритма. Новые значения оптимальных управлений при уменьшении шага h вычисляются в программной реализации, представленной в листинге 3. интерпретируются как одномерные массивы W1[n], W2[n], … Для каждого из них существует массив копий W1_old[n], W2_old[n], …, в котором хранятся оптимальные значения, полученные на предыдущем шаге алгоритма. Новые значения оптимальных управлений при уменьшении шага h вычисляются в программной реализации, представленной в листинге 3.
Листинг 3. Уменьшение шага h
for (int q = 0; q <= N - 1; q++) {
h = h / 2.0;
for (int n = 0; n <= N - 1; n++) {
Minimize(W1, n);
W1[n] = result[n];
}
}
После нахождения оптимальных управлений  программное приложение осуществляет запись полученных значений массивов W1[n], W2[n], … в соответствующие файлы «W1.txt», «W2.txt», … для дальнейшего их использования припостроении графиков в пакете прикладных программ математического моделирования. программное приложение осуществляет запись полученных значений массивов W1[n], W2[n], … в соответствующие файлы «W1.txt», «W2.txt», … для дальнейшего их использования припостроении графиков в пакете прикладных программ математического моделирования.
Сравним практические результаты прямого расчета с аналитическим решением задачи. Для проверки правильности кода результаты прямого расчета сравнивались с аналитическим решением с точностью ε = 10-4. В качестве примера взяты следующие исходные параметры: l = 1, a = 1, M1 = 20, M2 = 20, N = 40.
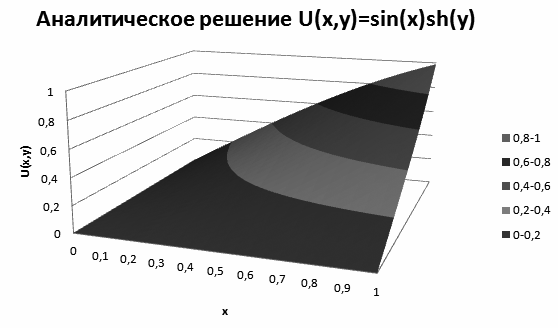
Рисунок 1. Аналитическое решение
На рис. 1 представлен график значений сеточной функции  , который полностью совпадает с графиком аналитического решения однородной задачи, которое имеет вид: , который полностью совпадает с графиком аналитического решения однородной задачи, которое имеет вид:

Примеры расчетов
Пример 1. В качестве примера рассматривается задача гашения колебаний мембраны с использованием одного точечного демпфера. В расчете принималось a = 1, l = 1, начальное положение демпфера (x1, y1) = (1/2, 1/2), hx = hy = 1/20, τ = 1/40. Начальные возмущения представлены функциями H0 = 4x(l1 – x)y(l2 – y).
Точность вычислений ε = 10-4. График строился в сечении y = 0,5 (см. рис. 2). Оптимальное управление W1(t), позволяющее погасить начальные колебания за время T = 2, показано на рис. 3.
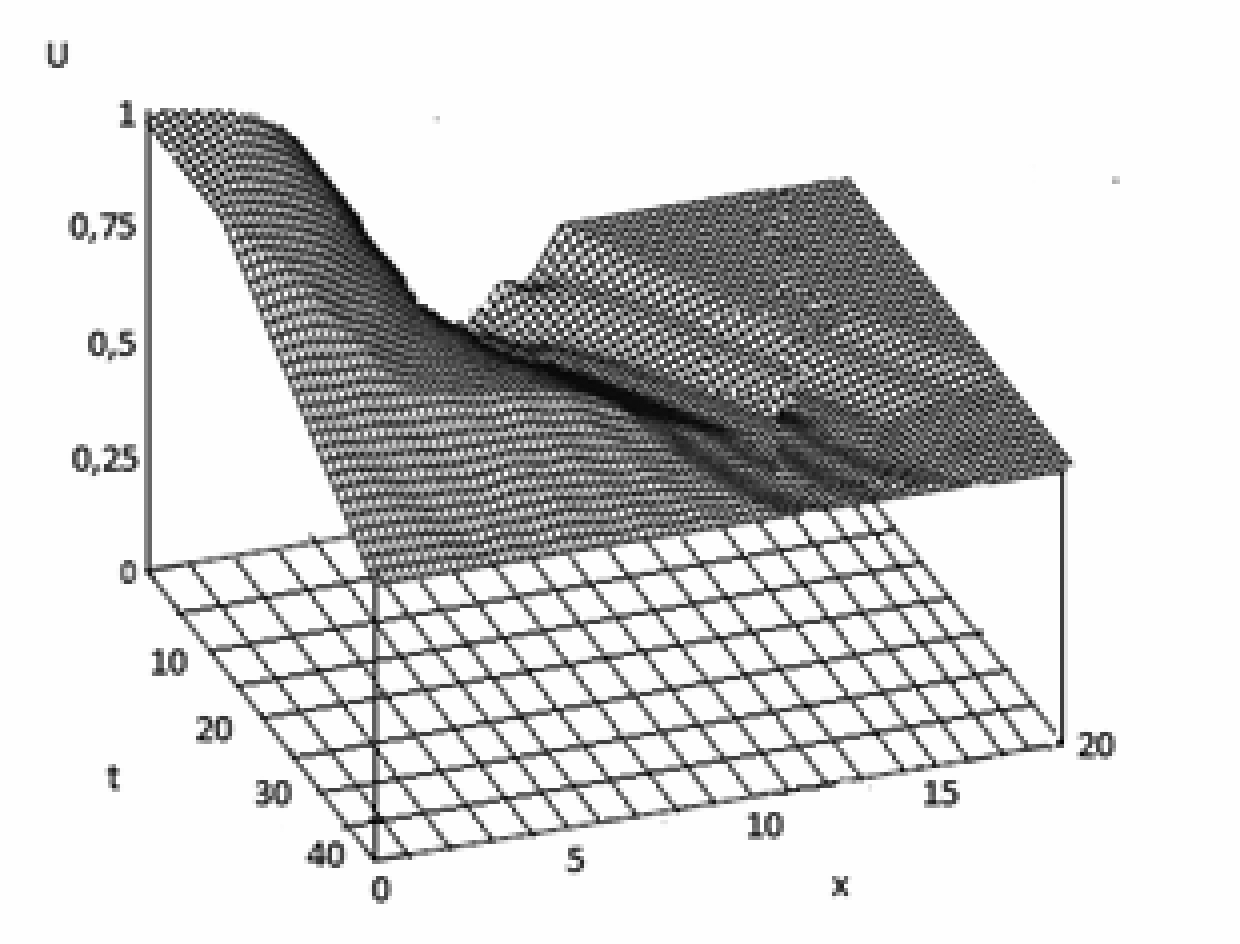
Рисунок 2. Процесс колебаний в сечении y = 0,5
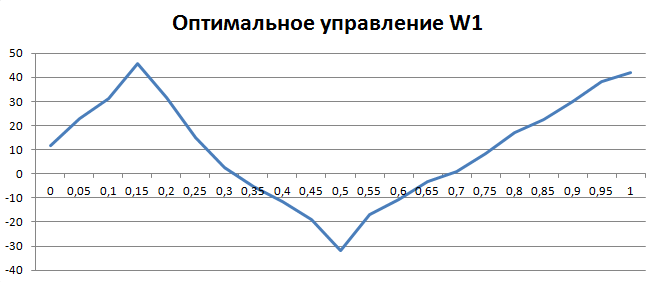
Рисунок 3. Оптимальное управление W1(t). T = 2
Пример 2. В данном примере были проведены расчеты с использованием одного точечного демпфера, но для более крупной сетки. Начальное положение демпфера (x1, y1) = (1/2, 1/2), hx = hy = 1/40, τ = 1/80. За время T = 1.8 происходит практически полное гашение колебаний. График строился в сечении y = 0,5 (см. рис. 4). График оптимального управления W1(t) представлен на рис. 5.
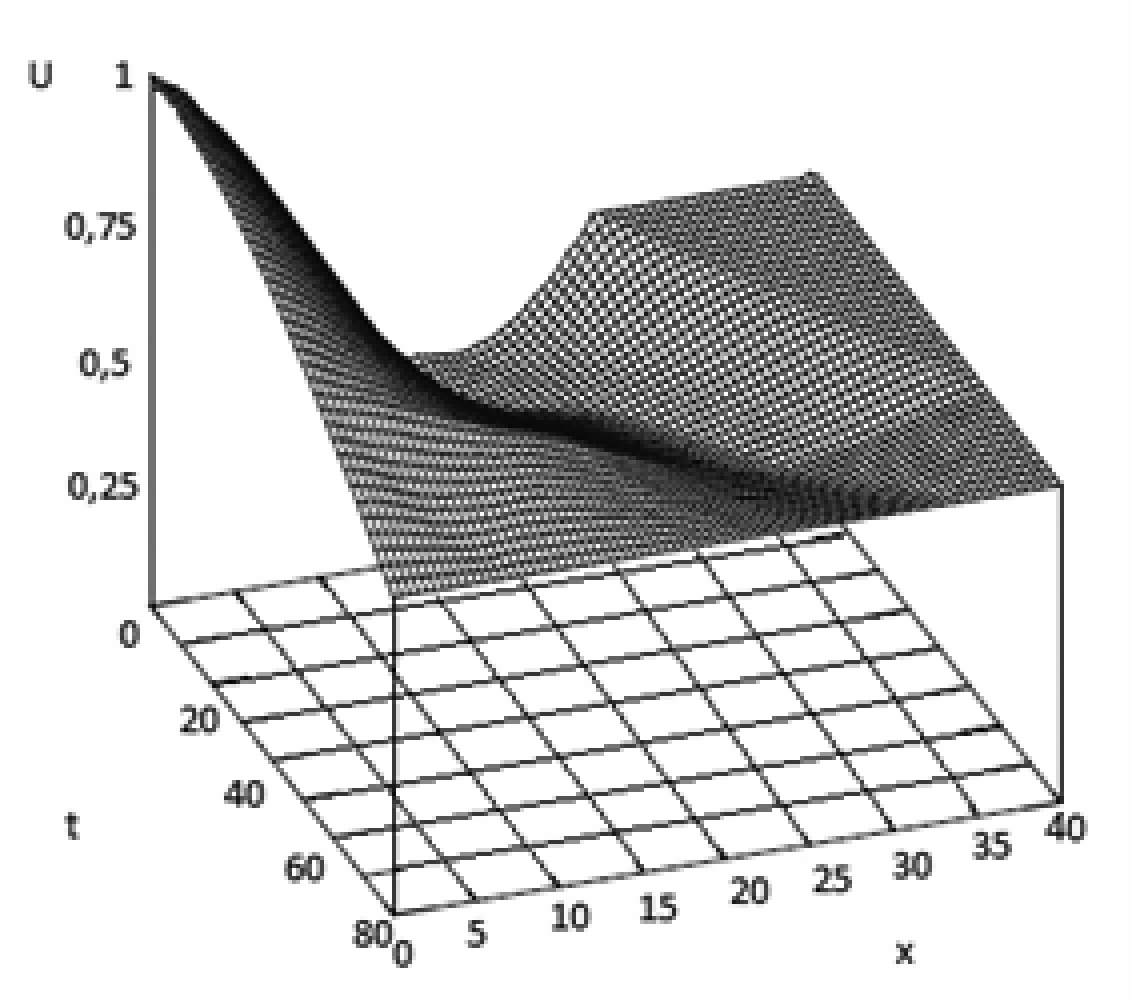
Рисунок 4. Процесс гашения в сечении y = 0,5
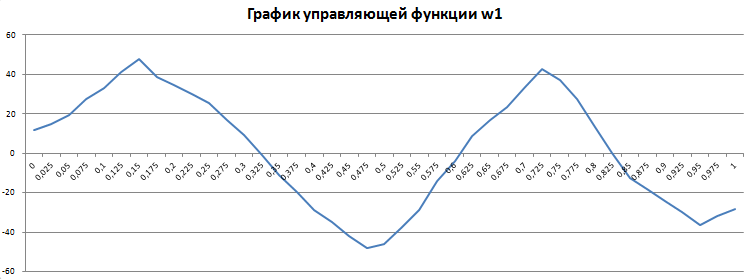
Рисунок 5. Оптимальное управление W1(t). T = 1.8
Рассмотрим аналитическое решение однородного уравнения для тестирования программного приложения решения задачи (1.1) – (1.3).
Для нахождения функции H0 из условий (1.2) решим следующую задачу:
 (П 1.1) (П 1.1)
при наличии условий начальных:
 (П 1.2) (П 1.2)
граничных:
 (П 1.3) (П 1.3)
Для этого воспользуемся методом Фурье, который базируется на разделении переменных в уравнении (П 1.1). Будем искать решение задачи в виде:
u(t, x) = T(t)X(x) (П 1.4)
Подставим вид функции u(t, x), представленный в виде (1.4), в исходное уравнение, получим следующее дифференциальное уравнение второго порядка:
 (П 1.5) (П 1.5)
Разделив переменные, получим:
 (П 1.6) (П 1.6)
Поскольку в уравнении (П 1.6) левая часть предполагает зависимость от t, а правая зависит только от x, то знак равенства между ними может иметь смысл при условии, что обе части равны постоянной:
 (П 1.7) (П 1.7)
В этом случае можно записать два дифференциальных уравнения:

Решим первое из этих уравнений с учетом начальных условий:
 (П 1.8) (П 1.8)
Общее решение дифференциального уравнения (П 1.8) будет иметь вид: X(x) = Acosλx + Bsinλx
Постоянные A, B находим из начальных условий в системе (П 1.8): A = 0, B = 1.
Таким образом, собственными числами задачи (П 1.8) будут λn = πn/l, а соответствующие им собственные функции Xn(x) = sin(λnx), n=1, 2, …
Задача
 (П 1.9) (П 1.9)
имеет решение вида: T(t) = Ccos(λnat) + Dsin(λnat).
С учетом начальных и граничных условий (П 1.2) и (П 1.3) соответственно общее решение задачи будет иметь вид:

- Марченко В.М. Температурные поля и напряжения в конструкциях летательных аппаратов. – Москва. Машиностроение, 1965.
- Lagness J. Control of wave process with distributed controls supported on a subregion // SIAM Journ. Control and Optim. 1983. Vol. 1, no. 1. Pp. 68-85.
- Russel D.L. Controllability and stabilization theory for linear partial differential equations // SIAM Review. 1978. Vol. 20, no. 5. Pp. 639-739.
- Бутковский А.Г. Методы управления системами с распределенными параметрами. – Москва. Наука, 1975. – 366 с.
- Бутковский А.Г. Приложение некоторых результатов теории чисел к проблеме финитного управления и управляемости в распределенных системах // ДАН СССР. 1976. Т. 227, № 2. – С. 309-311.
- Muravey L.A. Mathematical problems on the damp of vibration // Preprint of IFAC Conference «Identification and system parameter estimations». 1991. Vol. 1. Pp. 746-747.
- Levinson N. Gap and density theorem // Amer. Math. Soc. Colog. Publ. 1940. Vol. 26.
- Ильин В.А., Моисеев Е.И. Оптимизация граничных управлений колебаниями струны // Успехи математических наук. 2005. Т. 60, № 6. – 89 с.
Ключевые слова: колебания, демпфер, мембрана, краевая задача, волновое уравнение, метод сеток, метод аппроксимации, градиент, метод Лагранжа, С#, условие устойчивости на Нейману, метод квадратичной параболы, метод координатного спуска, метод Фурье, дельта-функция Дирака.
Development of vibration damping methods using point stationary dampers. Part 2. Fluctuations of a flat membrane
Troenko S.Yu., Moscow Aviation Institute (National Research University), bachelor, 813 department
Povalyaev P.P., Moscow Aviation Institute (National Research University), 812 department, engineer
Abstract: In this paper we consider the problem of damping vibrations of a plane membrane using several point dampers. Methods for damping vibrations of a plane membrane using several point stationary dampers for arbitrary initial perturbations are proposed. As the boundary conditions, the fastening conditions are considered. A numerical algorithm for solving the problem of damping vibrations of a plane membrane using a coordinate method is developed. A software application has been developed that implements numerical methods and visualizes the main results of this work for different values of the initial data. The application is written in C #.
Keywords: oscillations, damper, membrane, boundary value problem, wave equation, grid method, approximation method, gradient, Lagrange method, C #, Neumann stability condition, quadratic parabola method, coordinate descent method, Fourier method, Dirac delta function.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
