ЗИМИНА Е.Ю., Национальный исследовательский университет «Высшая школа экономики», Московский институт электроники и математики им. А.Н. Тихонова, Таллинская, 34, Москва, Россия, 123458; ЗАО «ЕС-Лизинг», Варшавское шоссе, 125, с.1, Москва, Россия, 117405

 НОВОПАШИН М.А., ЗАО «ЕС-Лизинг», Варшавское шоссе, 125, с.1, Москва, Россия, 117405

 ШМИД А.В., Национальный исследовательский университет «Высшая школа экономики», Московский институт электроники и математики им. А.Н. Тихонова, Таллинская, 34, Москва, Россия, 123458; ЗАО «ЕС-Лизинг», Варшавское шоссе,125, с.1, Москва, Россия, 117405

Кластеризация медицинских больших данных
как инструментарий систем поддержки принятия решений в математической кардиологии с использованием облачных технологий

Массовое использование мобильных устройств для съема электрокардиограмм (ЭКГ) приводит к количественному росту доступных для исследования ЭКГ пациентов. Таким образом, появляются новые возможности исследования колебательных процессов долговременной динамики индивидуального состояния сердечно-сосудистой системы (ССС) любого пациента

В статье демонстрируются новые возможности долговременного постоянного наблюдения за состоянием ССС массы пациентов, позволяющие выявить закономерности динамики ССС, которые приводят к выдвижению гипотезы осуществовании адекватной модели ССС как распределенной нелинейной автоколебательный системы класса моделей возвратов Ферми – Паста – Улама (ФПУ).

Наличие содержательной математической модели ССС возврата ФПУ, как уточнение традиционной модели изучения вариабельности сердечного ритма (ВСР), далее позволяет предложить новые вычислительные методы анализа ЭКГ ипрогнозирования динамики ССС для более детальной диагностики и оценки эффективности проводимого лечения

I. Введение

В применяемой модели сердца на основе явления возврата ФПУ базовыми традиционно являются понятия «состояния» сердца как регистрируемого колебательного процесса. Однако поскольку сердце является автоколебательной системой и ему не требуется для начала колебаний получения энергии «возмущения», то при исследовании сердца вводится понятие автовозврата ФПУ [1].

Идеальная ЭКГ в гипотетическом случае отсутствия любых внешних воздействий представляет собой периодически появляющийся автовозврат ФПУ, который характеризует состояние пациента.

В реальной же жизни различные физические и эмоциональные нагрузки, терапия и другое являются для модели сердца внешними «возмущениями» и эпизодически высвечиваются в картине автовозврата [2]. Их влияние на автовозврат теоретически может быть выявлено, давая возможность устанавливать биологически значимые параметры уравнений модели ФПУ, диагностируя фактическое биологическое состояние сердца.

Теоретически в модели ФПУ допускается бесконечное число состояний сердца. Реализация процесса кластеризации представляется конструктивным, так как из-за бесконечного числа состояний модели ФПУ сердца следует, что дляпрактического кардиолога все бесконечное множество картин автовозвратов состояний сердца должно укладываться в конечное число предполагаемых диагнозов.

Однако из модели ФПУ также следует, что реальная картина поведения сердца может оказаться несколько сложнее: в составе ЭКГ могут оказаться такие варианты поведения сердца, которые «не вписываются» ни в один из известных кластеров, а отражают процессы перехода сердца из состояния в состояние.

II. Выдвигаемая гипотеза

В данной работе сердце рассматривается как распределенная автоколебательная система, которая теоретически имеет бесконечное число автовозвратов ФПУ [3]. Так вводится понятие кластера, получаемого в процессе серии сравнений собственных спектров ЭКГ между собой и обнаружении повторяющихся. Это позволяет выделять схожие кластеры у разных пациентов: как у здоровых, так и у пациентов, которые имеют различные сердечные патологии. Гипотеза состоит втом, что предлагаемые кластеры могут быть использованы как для анализа различный патологий у пациентов, так и для оценки кардиологического статуса здоровых людей.

III. Понятие автовозврата ФПУ

Введем понятие автовозврата ФПУ на математическом уровне. Явление канонического возврата ФПУ в пассивных системах было впервые описано в результате численного исследования решений дифференциально-разностных уравнений, описывающих цепочку нелинейно связанных вибраторов [4].

В этих модельных цепочках явление затухания не было представлено. Для описания же реальных динамических процессов, таких как сердечная деятельность, требуется более подходящая модель, способная описать возвраты в автономно функционирующих или автоколебательных системах.

Значительным вкладом в этом направлении явилась работа американских исследователей Забуски и Крускала, которые предложили описать возврат ФПУ в рамках уравнения Кортевега де Вриза (КдВ) с периодически меняющимися граничными и начальными условиями [5]. Используя результаты данной работы, можно упростить решения уравнений КдВ в виде кноидальных волн, заменив их решениями уравнения Ван дер Поля, близкими к гармоническим, анизкочастотные периодические изменения граничных и начальных условий на релаксационные решения уравнения Ван дер Поля.

При этом если применить теорему о возможности замены волновых связей на запаздывающие [6], то можно в простейшем приближении представить математическую модель электрической активности сердца (ЭКГ) в виде автовозврата ФПУ, описываемого в рамках связанных уравнений Ван дер Поля с запаздыванием [7] в следующем виде:

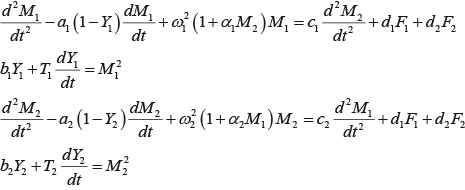
где:

• M₁ – величина, пропорциональная динамическому электрическому потенциалу всего миокарда;
• M₂ – величина, пропорциональная динамическому электрическому потенциалу небольшой локальности миоцитов на поверхности миокарда;
• Y₁ – величина, пропорциональная запаздыванию при распространении электрического импульса в миокарде;
• Y₂ – величина, пропорциональная запаздыванию при распространении электрического импульса в локальности миоцитов;
• b₁ – величина, пропорциональная площади поверхности миокарда;
• b₂ – величина, пропорциональная площади поверхности локальности миоцитов;
• T₁ – величина, пропорциональная времени сокращения миокарда;
• T₂ – величина, пропорциональная периоду колебаний в локальности миоцитов;
• F₁ – функция резонансного воздействия внешней среды на сердце на частоте сердцебиений (около 1 Гц);
• F₂ – функция резонансного воздействия внешней среды на сердце на высокой частоте около 20 Гц;
• c₁, c₂, d₁, d₂ – константы.

IV. Результаты исследований

A. Материал и методы исследований

В ходе исследования было проанализировано 14 500 кардиограмм пациентов в возрасте 42-60 лет со стенокардией напряжения (СН) различного функционального класса (ФК), из них 36 человек с типичным болевым синдромом и эпизодами безболевой ишемии миокарда (ББИМ) (мужчин – 25, женщин – 11) и 30 человек (мужчин – 18, женщин – 12) с типичным болевым синдромом, без эпизодов ББИМ.

Пациенты с постоянной формой фибрилляции предсердий исключались из исследования, а также исключались следующие пациенты:

• с полной атриовентрикулярной (а-в) блокадой,
• полной блокадой левой ножки пучка Гиса,
• техническими причинами ложно-негативной или ложно-позитивной детекции при идентификации ишемии миокарда (рекомендации по Холтеру),
• жизнеугрожающей аритмией,
• острым нарушением мозгового кровообращения,
• опухолями,
• анемией тяжелой степени,
• патологией щитовидной железы в стадии декомпенсации,
• отсутствием информированного согласия пациента,
• невозможностью проведения нагрузочных проб,
• с сомнительными результатами нагрузочных тестов и холтеровского мониторирования (ХМ) ЭКГ.

Диагноз ставился с учетом клинических, анамнестических, инструментальных методов исследования. Верификация диагноза осуществлялась с помощью проб с физической нагрузкой (велоэргометрия (ВЭМ) или стресс-эхокардиография). Всем больным проводилось ХМ ЭКГ.

B. Обработка электрокардиограмм

Исследование кардиограмм необходимо для получения расчетов, на основе которых будут произведены анализ состояния пациента и прогнозирование его состояния. Обработка новой поступившей кардиограммы производится впоследовательном выполнении нескольких видов заданий:

• подготовка кардиограммы к дальнейшим расчетам;
• расчет спектра Фурье и его характеристик (гармоники и энергии) для нефильтрованного сигнала, сигнала с исправленной изолинией и сигнала с исправленной изолинией и очищенного от дефектов;
• расчет формы спектра для сигнала с исправленной изолинией и очищенного от дефектов;
• перерасчет кластеров кардиограмм во всей серии кардиограмм пациента с различными параметрами кластеризации;
• расчет показателей тенденции пациента (биологического возраста).

Обработка обновленного множества всех кардиограмм производится по расписанию и для различных целевых групп по возрасту, полу, информации о патологиях для различных параметров кластеризации.

Возрастные группы выделяются следующие: все возраста и пять отдельных возрастных групп от молодых к старым. Группы по полу выделяются следующие: мужчины и женщины.

По патологиям выделяются следующие группы:

• размеченная выборка кардиограмм по диагнозу ишемия (подтвержденная и не подтвержденная);
• размеченная выборка кардиограмм по диагнозу туберкулез (подтвержденная и не подтвержденная);
• размеченная выборка кардиограмм по диагнозу диабет (подтвержденная и не подтвержденная).

Если в группе с момента выполнения последней кластеризации не появилось новых кардиограмм, запуск новой кластеризации не производится.

При обработке отдельной кардиограммы перед проведением расчетов и исследования у нее необходимо исправить изолинию, т.е. удалить дрейф изолинии, и очистить ее от сильных дефектов, т.к. это очень портит частотные характеристики кардиограммы, необходимый необходимые для дальнейшего анализа.

Дрейф изолинии удаляется двухмедианным методом, для этого из исходного сигнала поэлементно вычитается рассчитанная посредством двух медиан изолиния.

C. Принципы построения кластеров

Под кластером подразумевается набор из одной и более ЭКГ и связанная с этим набором, средняя арифметическая форма спектра, рассчитанная автоматически в результате процесса упорядоченной классификации ЭКГ.

Сравнение Фурье-спектров ЭКГ производилось на основе явления возврата ФПУ, на основе визуального восприятия спектра. Для этого было введено понятие формы спектра [8]. Форма спектра – сглаженная кривая, основанная на медиане верхних 30% значений в окне 2 Гц, взятая в диапазоне от 0 до 40 Гц. Ширина окна 2 Гц взята специально для исключения влияния выраженных гармоник для ЭКГ с частотой пульса менее 120 уд/мин. Форма спектра используется вдальнейшем в алгоритме определения областей ишемии и кластеризации ЭКГ по форме спектра.

Для кластеризации форма аппроксимируется с шагом 0,1 Гц до 400 точек и нормализуется по среднему арифметическому для универсальности сравнения.

Кластеризация ЭКГ по форме спектра производится методом выделения связных компонент [9]. Расстояние между формами спектра сравниваемых ЭКГ берется евклидово. В процессе кластеризации исходный полносвязный граф приотбрасывании связей большей длины, чем заданное заранее значение, рассыпается на группу подграфов, которые и образуют в результате искомые кластеры.

Для упрощения алгоритма кластеры формируются автоматически на основе классификации ЭКГ по мере их поступления (так называемый онлайн-метод) [10]. В этом случае подразумеваются операции дополнения кластера новой формой ЭКГ, создания нового кластера и объединения кластеров на основе расстояния между ними.

Практически получено, что всегда присутствует кластер с преобладающим количеством ЭКГ, попавших в него. Предположительно ЭКГ этого кластера характеризуют обычное состояние пациента. ЭКГ, попавшие в остальные кластеры, характеризуют в той или иной степени аномальное состояние пациента, вызванное как внешним стрессовым воздействием, так и патологиями. Часто встречаются кластеры, состоящие из одной ЭКГ, – их появление позволяет судить оперемежаемости сложных автовозвратов ФПУ у пациента (когда между повторениями определенного состояния происходит смена нескольких состояний, отличных от повторяемого).

Кластер с наибольшим набором ЭКГ называется базовым кластером. Для всех остальных кластеров вводится мера отклонения кластера от базового в виде евклидового расстояния между соответствующими усредненными формами.

Для таких точек отсчета выбраны несколько кластеров здоровых людей, пациентов с ишемической болезнью сердца (ИБС). На рис.1 приведен типичный Фурье-спектр ЭКГ здорового человека. На рис.2 приведен типичный Фурье-спектр ЭКГ пациента с развитым ишемическим процессом.

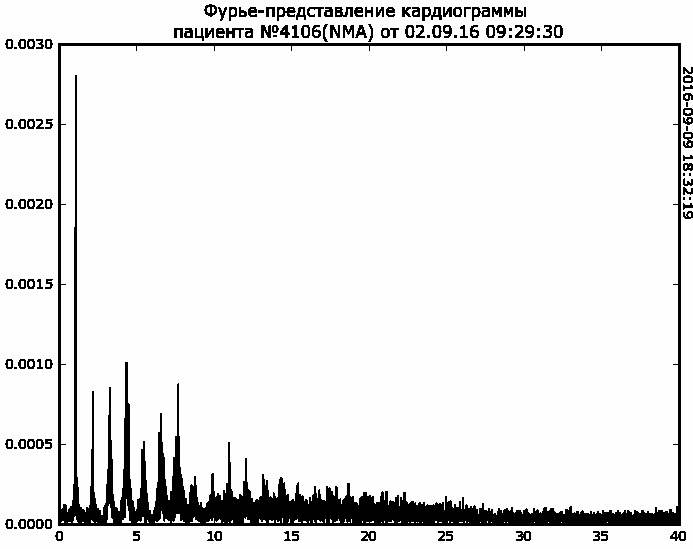
Рисунок 1. Типичный Фурье-спектр ЭКГ здорового сердца. Горизонтальная ось – частота в Гц, вертикальная ось – потенциал мв

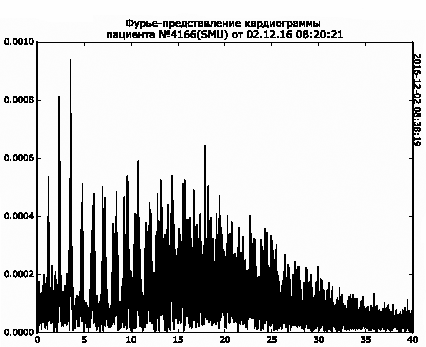
Рисунок 2. Типичный Фурье-спектр ЭКГ пациента с развитым ишемическим процессом. Горизонтальная ось – частота в Гц, вертикальная ось – потенциал мв

Развитый ишемический процесс в соответствии с гипотезой представляет собой формирование автономной динамической системы в миокарде, обладающей колебательными параметрами, отличными от параметров колебаний в нормальной ткани миокарда. В частности, основные частоты спектра ЭКГ нормально функционирующего сердца лежат в диапазоне 1-12 Гц, в то время как спектр ишемического процесса находится в диапазоне 14-20 Гц и может динамически изменяться.

На основе характерных признаков отдельных полученных кластеров и данных о патологиях пациентов выделяются кластеры, схожие по характеристикам формы спектра, и выводятся в отдельные группы по патологиям.

Таким образом, метод кластеризации может быть использован для диагностики ИБС, определения кардиологического статуса здоровых людей.

V. Заключение

Результаты экспериментальных исследований показали, что гипотеза о том, что предлагаемые кластеры могут быть использованы как для анализа различный патологий у пациентов, так и для оценки кардиологического статуса здоровых людей, нашла свое подтверждение. В частности, использование кластеров позволило не только диагностировать ИБС у пациентов с различной степенью развития ишемического процесса, но и оценивать у них уровень сердечной недостаточности.

Таким образом, использование кластерного подхода может быть полезным для диагностики различных степеней ИБС, определения кардиологического статуса здоровых людей с оценкой его возрастных изменений. Помимо этого, предлагаемый кластерный метод позволит оценить действие применяемой терапии в динамике и изменять ее в случае неэффективности.

1. Fermi E., Pasta J., Ulam S. In: Collected Papers of E. Fermi. – 1955. – Vol. 2, 978 P.
2. Berezin, A.A. Resonant interaction between the Fermi-Pasta-Ulam recurrences.// Bulletin of the Lebedev Physics Institute. FIAN. – 2004. – N. 3. – P. 13.
3. Novopashin M.A., Shmid A.V. D.SC. Berezin A.A. PhD, Forrester’s Concept in Modeling Heart Dynamics. // IOSR Journal of Computer Engineering. – May-Jun. 2017. – Vol. 19. – Issue 3, Ver.2.
4. Форрестер Д. Мировая динамика. – М.: АСТ, 2006. – С. 384. – ISBN 5-17-019253-3.
5. Н.А. Кудряшов. Точные решения уравнения N-го порядка с нелинейностью Бюргерса – Кортевега – де Вриза. Матем. моделирование, 1:6 (1989), 57-65 c.
6. Wiener N. The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle / N. Wiener, A. Rosenblueth // Arch. Del. Instit. De Cardiologia De Mexico, 1946. P. 205-265.
7. Van der Pol B, Van der Mark M. Le battement du coeur considere comme oscillation de relaxation et un model elecrtrique du coeur. L’Onde electrique, 1928, N 7.
8. Факторный, дискриминантный и кластерный анализ / Дж.-О. Ким, Ч.У. Мьюллер, У.Р. Клекка и др. – М.: Финансы и статистика, 1989. – 215 c.
9. Shmid A., Berezin A., Novopashin M. Coupled blood pressure dynamics in magisterial and small arteries networks and its stabilizing effect on heart functioning within the framework of computer model // Annals of Circulation. 2018. No. 3. P. 4-7.
10. Shmid A., Pozin B., Ageykin M. Teaching Big Data Technology Practices in Cloud Environment, in: Smart Education and e-Learning 2016 Issue 59. Switzerland : Springer International Publishing, 2016. P. 631-639.

Ключевые слова: кардиология, большие данные, кластерный анализ, математическая кардиология.

Clustering of medical big data as a tool for decision support systems in mathematical cardiology using cloud technologies

Zimina E.Yu., National Research University "Higher School of Economics", Moscow State University of Electronics and Mathematics A.N. Tikhonova, Tallinskaya, 34, Moscow, Russia, 123458; CJSC "EU-Leasing", Warsaw highway, 125, p.1, Moscow, Russia, 117405

Novopashin M.A., ZAO "EU-Leasing", Warsaw highway, 125, p.1, Moscow, Russia, 117405

Shmid A.V., National Research University "Higher School of Economics", Moscow Institute of Electronics and Mathematics A.N. Tikhonova, Tallinskaya, 34, Moscow, Russia, 123458; CJSC "EU-Leasing", Warsaw highway, 125, p.1, Moscow, Russia,117405

Abstract: Mass use of mobile devices for the removal of electrocardiograms (ECG) leads to a quantitative increase in the number of patients available for ECG study. Thus, new opportunities arise for studying the oscillatory processes of the long-term dynamics of the individual state of the cardiovascular system (CVS) of any patient.

Keywords: cardiology, large data, cluster analysis, mathematical cardiology.

Комментарии могут оставлять только зарегистрированные пользователи