|
Рубрика:
Наука и технологии
|
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
 ТРОЕНКО С.Ю., Московский авиационный институт (национально исследовательский университет), бакалавр, 813-я кафедра ТРОЕНКО С.Ю., Московский авиационный институт (национально исследовательский университет), бакалавр, 813-я кафедра
 ПОВАЛЯЕВ П.П., Московский авиационный институт (национально исследовательский университет), 812-я кафедра, инженер ПОВАЛЯЕВ П.П., Московский авиационный институт (национально исследовательский университет), 812-я кафедра, инженер
Разработка методов демпфирования колебаний
с помощью точечных стационарных демпферов. Часть 1. Колебания струны
В данной статье рассматривается задача гашения колебаний струны с использованием нескольких точечных демпферов. Предложены методы гашения колебаний струны с использованием нескольких точечных стационарных демпферов дляпроизвольных начальных возмущений. В качестве краевых условий рассмотрены условия закрепления. Разработан численный алгоритм решения задачи гашения колебаний струны для нахождения оптимального управления, а именно сиспользованием градиентного метода, причем градиент вычислялся с помощью быстрого автоматического дифференцирования. Разработано программное приложение, реализующее численные методы и визуализирующие основные результаты данной работы при различных значениях начальных данных. Приложение написано на языке С#
Задачи гашения колебаний и, в частности, колебаний тонких длинных элементов актуальны в силу многочисленных технических приложений. При создании новых космических комплексов в мировой практике все более широкое применение находят космические платформы (КП), на которых размещаются различного вида полезные нагрузки. Сами КП имеют каркасную конструкцию, кроме того, в большинстве проектов КП имеются выносные конструкции, такие как антенные устройства или панели солнечных батарей. На борту КП размещаются приборы и агрегаты технологических систем, которые могут быть источниками механических возмущений, способствующих возникновению вынужденных упругих колебаний составных частей КП. Кроме того, эти колебания могут возникать после соударения стыковочных механизмов. Это вызывает влияние на пространственную устойчивость КП и отрицательно влияет наработу установленных на ней приборов. Поэтому гашение таких колебаний представляет собой важную прикладную задачу.
Колебание струны
Колебания струны описываются гиперболическим уравнением:
 (1.1) (1.1)
с начальными условиями:
 (1.2) (1.2)
которые будем считать начальными возмущениями и граничными условиями (условиями закрепления):
 (1.3) (1.3)
Энергия колебаний струны в момент времени t выражается следующим интегралом:
 (1.4) (1.4)
Поставим задачу гашения колебаний струны следующим образом: необходимо найти функцию g(t, x) из класса L2 (0 ≤ t ≤ T, 0 ≤ x ≤ l), позволяющую перевести струну из состояния (1.2) в состояние покоя:
 (1.5) (1.5)
за минимальное время T > 0.
Заметим, что условие (1.5) равносильно обращению интеграла энергии струны в ноль в момент времени T с учетом условий (1.3):
 (1.6) (1.6)
Основная идея статьи заключается в использовании нескольких точечных демпферов.
Будем искать функцию g(t, x) в виде:
 (1.7) (1.7)
где
- Wi – управляющие функции,
- δ – дельта-функция Дирака,
- xi – точки, в которые помещаются демпферы.
Потребуем также, чтобы функции Wi(t) были ограничены некоторым значением Wmax:
 (1.8) (1.8)
Рассмотрим численные методы решения задачи гашения колебаний.
Численный алгоритм решения начально-краевой задачи для волнового уравнения
Для численного решения дифференциального уравнения (1.1) применяется метод сеток, или разностный метод.
Рассмотрим задачу о приближенном вычислении производных функции u(x, t), определенной и имеющей непрерывные вторые частные производные uxx на отрезке [a; b] и utt на отрезке [c; d]. Зададим натуральные числа M и N и разобьем рассматриваемые отрезки {0 ≤ x ≤ l, 0 ≤ t ≤ T} на промежутки точками xm и tn соответственно:
 (2.2) (2.2)
где h = l/M и τ = T/N – шаги сетки по переменным x и t соответственно. В качестве сетки Dh, τ используем совокупность точек пересечения прямых ωh х ωτ. Искомой сеточной функцией является таблица {u(mh, nτ)} значений решения u(x, t) задачи (1.1) – (1.3).
Обозначим
 (2.3) (2.3)
 (2.4) (2.4)
Вторую производную uxx можно приближенно заменить второй разностной производной в точке (xm, tn) ∈ (ωτ, ωh):
 (2.5) (2.5)
Разложение по формуле Тейлора имеет следующий вид:
 (2.6) (2.6)
Таким образом, разностная схема (2.5) аппроксимирует производную u''(xm, tn) со вторым порядком:

Аппроксимация второй частной производной utt осуществляется аналогично и также имеет второй порядок:
 (2.7) (2.7)
Введя обозначения  , с учетом вышесказанного уравнение (1.1) запишем в виде: , с учетом вышесказанного уравнение (1.1) запишем в виде:
 (2.8) (2.8)
Введем вместо точного решения u(xm, tn) сеточную функцию  , которая будет удовлетворять следующему конечно-разностному соотношению: , которая будет удовлетворять следующему конечно-разностному соотношению:
 (2.9) (2.9)
Согласно (2.8) оно аппроксимирует (1.1) со вторым порядком по h и τ.
Выразим  : :
 , где , где  . .
Аппроксимируем начальные условия (1.2). Первое начальное условие запишется в виде:

Для того чтобы аппроксимировать второе начальное условие (1.2), введем фиктивный слой t = –τ. Будем полагать, что уравнение (1.1) справедливо на промежутке [–τ; 0]. Решение на этом слое обозначим  . Аппроксимируем начальные условия со вторым порядком аппроксимации и выпишем разностную схему на слое n = 0: . Аппроксимируем начальные условия со вторым порядком аппроксимации и выпишем разностную схему на слое n = 0:

Выразим из первого уравнения  и подставим во второе уравнение: и подставим во второе уравнение:

Получим выражение для  : :

Краевые условия имеют вид:
 (2.10) (2.10)
В результате конечно-разностная аппроксимация уравнения (1.1) и начальных условий (1.2) имеет второй порядок аппроксимации.
Покажем, что составленная разностная схема (2.9) устойчива по Нейману.
Будем искать решение (2.9) в виде:
 (2.10) (2.10)
Условие устойчивости по Нейману имеет вид  для всех для всех  . Тогда разностная схема после сокращений будет иметь вид: . Тогда разностная схема после сокращений будет иметь вид:
 (2.11) (2.11)
В силу неравенства eipm ≠ 0 поделим соотношение (2.11) на eipm:

или

Применяя формулу Эйлера:

получим квадратное уравнение следующего вида:

или
 (2.12) (2.12)
По теореме Виета для приведенного квадратного уравнения имеем:
 (2.13) (2.13)
Применяя формулу двойного угла для cos p:  получим: получим:  . .
Тогда соотношение (2.12) примет вид:
 (2.14) (2.14)
Если  , то уравнение имеет различные вещественные корни λ1 ≠ λ2, поэтому из условий (2.13) модуль одного из корней будет больше 1. Этот случай нас не устраивает. Если , то уравнение имеет различные вещественные корни λ1 ≠ λ2, поэтому из условий (2.13) модуль одного из корней будет больше 1. Этот случай нас не устраивает. Если
 (2.15) (2.15)
корни уравнения будут комплексно-сопряженными, причем  в силу условий (2.13). в силу условий (2.13).
Запишем неравенство (2.15) в виде:

Правое неравенство выполняется при любых p. Из левого неравенства следует:

Следовательно,
 (2.16) (2.16)
а значит, схема устойчива, если шаг по времени удовлетворяет неравенству (2.16).
Численный алгоритм выбора оптимального управления
Для численного расчета интеграла энергии струны воспользуемся следующей аппроксимацией:
 (2.17) (2.17)
Условием гашения будем полагать выполнение неравенства I(T) ≤ ε, где ε – заданная точность вычислений.
Аппроксимируем управляющие функции Wi(T) кусочно-постоянными функциями, такими как 
 (2.18) (2.18)
Тогда интеграл энергии (2.17) будет являться функцией переменных  : :
 (2.19) (2.19)
Оптимальные значения  , минимизирующие интеграл энергии с заданной точностью ε и являющиеся искомым решением задачи, будем искать методом градиентного спуска: , минимизирующие интеграл энергии с заданной точностью ε и являющиеся искомым решением задачи, будем искать методом градиентного спуска:
 (2.20) (2.20)
Градиент будем находить с помощью быстрого автоматического дифференцирования, предложенного Ю.Г. Евтушенко. Опишем идею быстрого автоматического вычисления градиента функции I(u, W), где u – решение некоторой начально-краевой задачи G(u, W) = 0, а W – управление. Пусть связи G(u, W) = 0 неявным образом определяют решение u = u(W). Тогда
 (2.21) (2.21)
Из уравнения (2.21) следует:
 (2.22) (2.22)
Градиент I(u, W) по управлению W определяется так:
 (2.23) (2.23)
Введем функцию Лагранжа:
 (2.24) (2.24)
Стационарные точки L определяются из равенств:
 (2.25) (2.25)
Из первого уравнения системы (2.25):
 (2.26) (2.26)
Тогда выражение для градиента примет вид:
 (2.27) (2.27)
Так как IW = 0, то

Итак, будем искать минимум функционала (2.17), причем конечно-разностное уравнение, начальные и краевые условия рассматриваются как связи.
Выпишем функцию Лагранжа, учитывая связи с помощью переменных множителей Лагранжа  : :
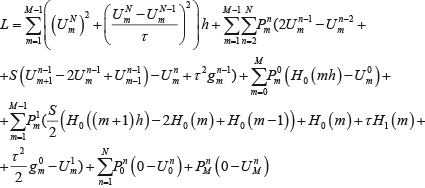 (2.28) (2.28)
Стационарные точки функции Лагранжа определяются из соотношений
 , где: , где:
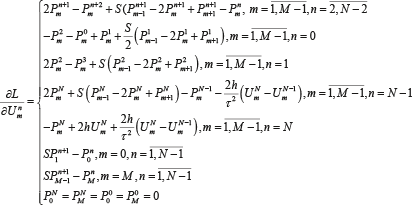 (2.29) (2.29)
Тогда множители Лагранжа  определяются следующим образом: определяются следующим образом:
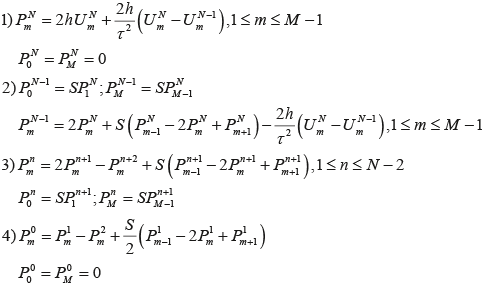
И градиент gradI находится по формулам:
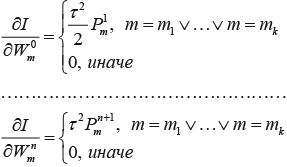 (2.30) и (2.31) (2.30) и (2.31)
Если τ → 0 и h → 0, то значения  являются решениями уравнения являются решениями уравнения
 (2.32) (2.32)
с начальными краевыми условиями:
 (2.33) (2.33)
где φ(U) – известная функция.
Легко видеть, что эта задача аналогична задачам (1.1), (1.2). Таким образом, чтобы вычислить gradI, достаточно один раз решить задачи (2.32), (2.33) с использованием разностных уравнений (2.29) и сразу выписать значение градиента поформулам (2.30), (2.31).
Опишем программное приложение. Программное приложение реализовано средствами объектно-ориентированного языка C#. Основной функцией программы является расчет оптимального управления для задачи гашения колебаний струны.
В качестве входных параметров программа использует размеры сетки M и N, описанной в пункте 1 настоящего параграфа, а также параметр α, необходимый для метода градиентного спуска в формуле (2.20). В качестве выходных параметров представлены файлы формата .txt, содержащие оптимальные значения.
Программа реализует следующие функции:
- прямой расчет – получение значений функции U;
- вычисление интеграла энергии колебаний струны;
- обратный расчет – вычисление коэффициентов P;
- минимизация интеграла энергии колебаний методом градиентного спуска.
Приложение не имеет значительных функциональных ограничений, однако предназначено для использования лишь на некоторых операционных системах семейства Windows и не подходит для реализации на операционных системах семейства Unix.
Алгоритм программной реализации выглядит следующим образом:
- Проводим прямой расчет значений функции U.
- Вычисляем значение интеграла энергии колебаний струны.
- Проводим обратный расчет коэффициентов P.
- Находим значение градиента по формулам (2.30), (2.31).
- Задаем значение параметра α – шага градиентного спуска.
- Вычисляем оптимальные значения по формуле (2.20).
- Снова проводим прямой расчет значений функции U.
- Сравниваем значение полученного нового интеграла энергии с его старым значением по абсолютной величине. Если значение нового интеграла меньше старого значения, запоминаем полученные значения
 и переходим к пункту 3, то есть проводим снова обратный расчет, в противном случае задаем новое значение параметра α (уменьшаем его) и вычисляем оптимальные значения и переходим к пункту 3, то есть проводим снова обратный расчет, в противном случае задаем новое значение параметра α (уменьшаем его) и вычисляем оптимальные значения  по формуле (2.20). по формуле (2.20).
Прямой расчет значений функции U осуществляется функцией GetU().
Для программной реализации сеточная функция  интерпретируется как двумерный массив U[m, n], поэтому заполнение ее значений осуществляется за счет цикла for(). интерпретируется как двумерный массив U[m, n], поэтому заполнение ее значений осуществляется за счет цикла for().
Начальные условия, которые воспринимаются в качестве начальных возмущений колебаний струны, заданы в функциях GetH0() и GetH1().
Программный код функции GetU() представлен для ознакомления в листинге 1.
Листинг 1. Прямой расчет в функции GetU()
for (int n = 0; n <= N; n++){
U[0, n] = 0; U[M, n] = 0;
}
for (int m = 1; m <= M; m++) {
U[m, 0] = GetH0(m * h);
GetG(m, 0);
U[m, 1] = U[m, 0] + tau * GetH1(m * h) + S / 2.0 * (GetH0((m + 1) * h) – 2 * GetH0(m * h) + GetH0((m – 1) * h)) + tau * tau / 2.0 * G[m, 0];
}
for (int n = 1; n <= N – 1; n++){
for (int m = 1; m <= M – 1; m++) {
GetG(m, n);
U[m, n + 1] = 2 * U[m, n] – U[m, n – 1] + S * (U[m + 1, n] – 2 * U[m, n] + U[m – 1, n]) + tau * tau * G[m, n];
}
}
Обратный расчет коэффициентов P осуществляется в функции GetP() посредством циклов for(), так как коэффициенты P также интерпретируются в качестве двумерного массива P[m, n].
Программный код функции GetP() представлен для ознакомления в листинге 2.
Листинг 2. Обратный расчет в функции GetP()
P[0, N] = -U[2, N] / (2.0 * a * h);
P[M, N] = -U[M – 2, N] / (2.0 * a * h);
P[1, N] = -1.0 / (2.0 * a * h) * (U[3, N] – U[1, N]) + 2 * h / (a * tau * tau) * (U[1, N] – U[1, N – 1]);
for (int m = 2; m <= M – 2; m++) {
P[m, N] = 1 / (a * h) * U[m, N] + 2 * h / (a * tau * tau) * (U[m, N] – U[m, N – 1]) – 1 / (2.0 * a * h) * (U[m – 2, N] + U[m + 2, N]);
}
P[M – 1, N] = 1 / (2.0 * a * h) * (U[M – 1, N] – U[M – 3, N]) + 2 * h / (a * tau * tau) * (U[M – 1, N] – U[M – 1, N – 1]);
P[0, N – 1] = S * P[1, N];
P[M, N – 1] = S * P[M – 1, N];
for (int m = 1; m <= M – 1; m++) {
P[m, N – 1] = 2 * P[m, N] + S * (P[m – 1, N] – 2 * P[m, N] + P[m + 1, N]) – 2 * h / (tau * tau) * (U[m, N] – U[m, N – 1]);
}
for (int n = N – 2; n >= 1; n--) {
for (int m = 1; m <= M – 1; m++)
P[m, n] = 2 * P[m, n + 1] – P[m, n + 2] + S * (P[m – 1, n + 1] – 2 * P[m, n + 1] + P[m + 1, n + 1]);
P[0, n] = S * P[1, n + 1];
P[M, n] = S * P[M – 1, n + 1];
}
P[0, 0] = 0;
P[M, 0] = 0;
for (int m = 1; m <= M – 1; m++){
P[m, 0] = P[m, 1]-P[m, 2]+S / 2.0 * (P[m – 1, 1] – 2 * P[m, 1] + P[m + 1, 1]);
}
Как было указано выше, вычисление градиента осуществляется по формулам (2.30), (2.31). С точки зрения реализации программного кода это выглядит следующим образом (см. листинг 3, случай использования двух точечных демпферов):
Листинг 3. Вычисление градиента (для двух демпферов)
LW1[0] = tau * tau / 2.0 * P[m1, 1];
LW2[0] = tau * tau / 2.0 * P[m2, 1];
for (int n = 1; n <= N – 1; n++){
LW1[n] = P[m1, n + 1] * tau * tau;
LW2[n] = P[m2, n + 1] * tau * tau;
}
Вычисление градиента в случае большего числа демпферов осуществляется аналогичным образом по формулам (2.30), (2.31).
Оптимальные значения  интерпретируются как одномерные массивы W1[n], W2[n], ... Для каждого из них существует массив копий W1_k[n], W2_k[n], ..., в котором хранятся оптимальные значения, полученные на предыдущем шаге алгоритма градиентного спуска. интерпретируются как одномерные массивы W1[n], W2[n], ... Для каждого из них существует массив копий W1_k[n], W2_k[n], ..., в котором хранятся оптимальные значения, полученные на предыдущем шаге алгоритма градиентного спуска.
Новые значения оптимальных управлений вычисляются по формуле (2.20) в программной реализации, представленной в листинге 4, где параметр alpha – выбранный шаг.
Листинг 4. Расчет оптимального управления
for (int n = 0; n <= N; n++){
W1[n] = W1_k[n] – alpha * LW1[n];
W2[n] = W2_k[n] – alpha * LW2[n];
}
После нахождения оптимальных управлений  программное приложение осуществляет запись полученных значений массивов W1[n], W2[n], ... в соответствующие файлы W1.txt, W2.txt,… для дальнейшего их использования припостроении графиков в пакете прикладных программ математического моделирования Matlab. программное приложение осуществляет запись полученных значений массивов W1[n], W2[n], ... в соответствующие файлы W1.txt, W2.txt,… для дальнейшего их использования припостроении графиков в пакете прикладных программ математического моделирования Matlab.
Для проверки правильности кода результаты прямого расчета сравнивались с аналитическим решением с точностью ε = 10-4. В качестве примера взяты следующие исходные параметры: l = 1, a = 1, M = 20, N = 80. На графике ниже синим цветом выделен график значений сеточной функции  , красным – график аналитического решения однородной задачи, имеющий вид: , красным – график аналитического решения однородной задачи, имеющий вид:

В качестве примера 1 рассматривается задача гашения колебаний струны с использованием одного точечного демпфера. В расчете принималось a = 1, l = 1, начальное положение демпфера x1 = 3/16, h = 1/16, τ = 1/32. Начальные возмущения представлены функциями H0 = sin2πx, H1 = 0. Точность вычислений ε = 10-4. Процесс гашения колебаний и оптимальное управление W1(t) позволяющее погасить начальные колебания за время T = 2, показаны на рис. 1 и 2 соответственно.
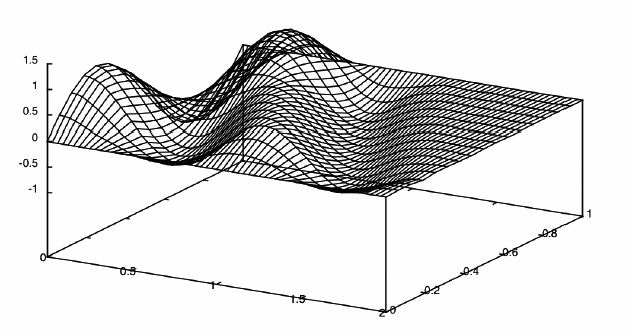
Рисунок 1. Процесс гашения колебаний. T=2
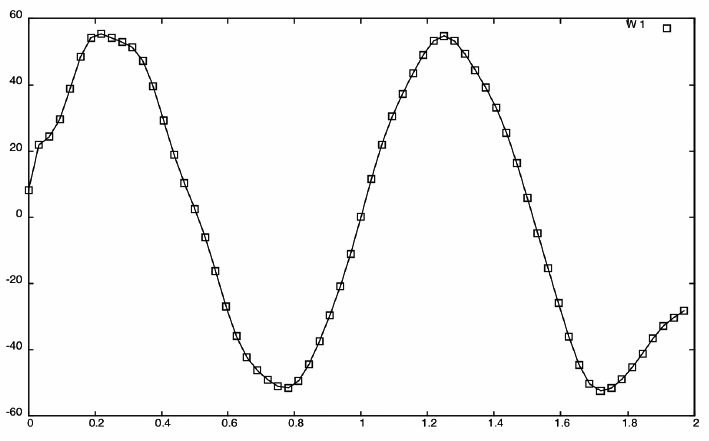
Рисунок 2. Оптимальное управление W_1 (t)
В примере номер 2 были проведены расчеты с теми же параметрами, что и в примере 1, но с использованием двух точечных демпферов. Начальные положения демпферов: x1 = 3/16, h = 1/16, τ = 1/32. За время T = 1.2 происходит практически полное гашение колебаний. Процесс гашения колебаний и графики оптимальных управлений W1(t), W2(t) представлены на рис. 3 и 4 соответственно.
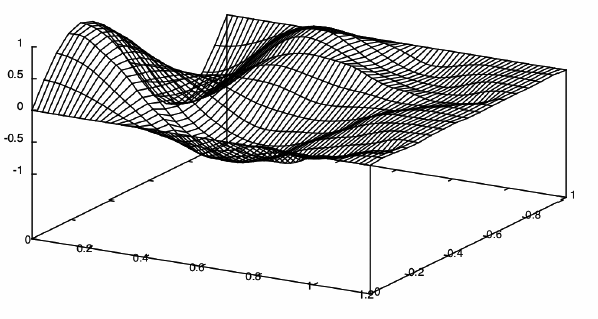
Рисунок 3. Процесс гашения колебаний. T=1.2
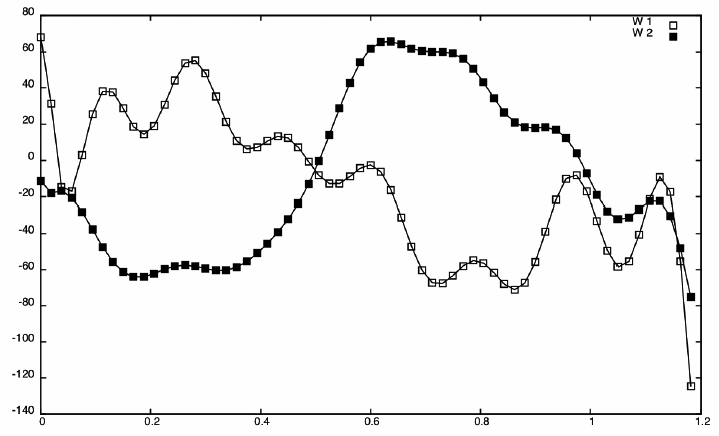
Рисунок 4. Оптимальные управления W_1 (t), W_2 (t)
- Марченко В.М. Температурные поля и напряжения в конструкциях летательных аппаратов. – М.: Машиностроение, 1965.
- Lagness J. Control of wave process with distributed controls supported on a subregion // SIAM Journ. Control and Optim. 1983. Vol. 1, no. 1. Pp. 68-85.
- Russel D. L. Controllability and stabilization theory for linear partial differential equations // SIAM Review. 1978. Vol. 20, no. 5. Pp. 639-739.
- Бутковский А.Г. Методы управления системами с распределенными параметрами. – М.: Наука, 1975. – 366 с.
- Бутковский А.Г. Приложение некоторых результатов теории чисел к проблеме финитного управления и управляемости в распределенных системах // ДАН СССР. 1976. Т. 227, № 2. – С. 309-311.
- Muravey L. A. Mathematical problems on the damp of vibration // Preprint of IFAC Conference «Identification and system parameter estimations». 1991. Vol. 1. Pp. 746-747.
- Levinson N. Gap and density theorem // Amer. Math. Soc. Colog. Publ. 1940. Vol. 26.
- Ильин В.А., Моисеев Е.И. Оптимизация граничных управлений колебаниями струны // Успехи математических наук. 2005. Т. 60, № 6. – 89 с.
Ключевые слова: колебания, демпфер, мембрана, краевая задача, волновое уравнение, метод сеток, метод аппроксимации, градиент, метод Лагранжа, С#, условие устойчивости на Нейману, метод квадратичной параболы, метод координатного спуска, метод Фурье, дельта-функция Дирака.
Development of vibration damping methods using point stationary dampers. Part 1. Vibrations of a string
Troenko S.Yu., Moscow Aviation Institute (National Research University), bachelor, 813 department
Povalyaev P.P., Moscow Aviation Institute (National Research University), 812 department, engineer
Abstract: In this paper, we consider the problem of quenching vibrations of a string using several point dampers. Methods for damping vibrations of a string using several point stationary dampers for arbitrary initial perturbations are proposed. As the boundary conditions, the fastening conditions are considered. A numerical algorithm for solving the problem of damping of oscillations of a string is developed to find the optimal control, namely, using the gradient method, and the gradient was calculated using fast automatic differentiation. A software application has been developed that implements numerical methods and visualizes the main results of this work for different values of the initial data. The application is written in C#.
Keywords: oscillations, damper, membrane, boundary value problem, wave equation, grid method, approximation method, gradient, Lagrange method, C #, Neumann stability condition, quadratic parabola method, coordinate descent method, Fourier method, Dirac delta function.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
