|
Рубрика:
Наука и технологии
|
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
 СОБЕНЕВСКИЙ А.П., Московский авиационный институт (национальный исследовательский университет), 812-я кафедра, техник СОБЕНЕВСКИЙ А.П., Московский авиационный институт (национальный исследовательский университет), 812-я кафедра, техник
 ПОВАЛЯЕВ П.П., Московский авиационный институт (национальный исследовательский университет), 812-я кафедра, инженер ПОВАЛЯЕВ П.П., Московский авиационный институт (национальный исследовательский университет), 812-я кафедра, инженер
Программный комплекс по решению
уравнений двухмерного пограничного слоя
Данная статья повествует о разработанной программе на языках C++ & C# по решению уравнений двухмерного пограничного слоя на поверхности ЛА при сверхзвуковых скоростях полета на основе методов квазилинеаризации и скалярной прогонки. Данная программа позволяет находить как локальные, так и интегральные параметры ламинарного, переходного и турбулентного пограничного слоя. Данные параметры необходимы для определения компонент аэродинамических характеристик ЛА с учётом вязких эффектов. В результате была получена расчетная программа (ядро) и графическая программа (GUI) для получения и обработки полученных данных. Дополнительно, в работе было представлено сравнение результата работы программы с реальными экспериментальными данными. Данное ПО можно использовать на различных предприятиях, которые специализируются на производстве деталей. Более того, на практически любых платформах, вне зависимости от уровня устаревания компьютеров на предприятии. В совокупности, это делает ПК не только уникальным, но и актуальным для предприятий в соответствующих сферах работы
Вопрос, который рассматривается в данной статье, является довольно важным не столько для теории, сколько для практики. Полное знание о характеристиках переходного слоя, который расположен между ламинарным и турбулентным течением, позволит построить полную и достоверную математическую модель процесса обтекания ЛА. Исследования обтекания ЛА с совершенным газом с учетом пограничного слоя осуществлено во множестве работ как для ламинарного, так и для турбулентного пограничного слоя. Однако влияние градиента давления во внешнем потоке изучено недостаточно полно. Данная статья посвящена изучению влияния градиента давления на характеристики пограничного слоя, в том числе и для вычисления начала перехода пограничного слоя. В качестве примера рассмотрена задача влияния градиента давления на начало перехода пограничного слоя. Для примерного понимания физической картины течения рассмотрим схему обтекания некоторого объекта.
Частицы жидкости, соприкасаясь с твердым телом, теряют скорость. По мере удаления от твердого тела скорость этих частиц возрастает и стремится к скорости набегающего потока. Отсюда и появляются силы трения от частиц, прикоторых появляется коэффициент трения (Cf) и коэффициент теплообмена. Картина течения около твердого тела представлена на рис. 1.
- Пограничный слой – в данном слое обычно существуют большие градиенты скорости по толщине слоя, достаточно велика сила трения ввиду того, что сила вязкости здесь практически максимальна.
- Спутный след – присутствуют большие градиенты скоростей, существует вязкость и трение. Течение здесь в основном имеет вихревой характер.
- Вне пограничного слоя – вязкость здесь довольно слабая, а градиент скорости и сила трения почти нулевые, поэтому ими часто пренебрегают при расчетах в данном слое. Более того, газ в этой зоне считают идеальным.

Рисунок 1. Схема течения потока вокруг твердого тела. (1) – тонкий (пограничный) слой, (2) – спутный след, (3) – течения вне пограничного слоя
Далее нас будут интересовать в основном пограничный слой и влияние градиента на него.
Между ламинарным и турбулентным пограничными слоями существует протяженная область переходного течения от ламинарного к турбулентному, на которое влияет температура поверхности, завихренность внешнего потока, шероховатость поверхности и пульсации скорости внешнего набегающего потока.

Рисунок 2. Схема течения с нанесением векторов потока
Физическая картина образования пограничного слоя при обтекании твердой поверхности состоит в следующем: равномерный поток без завихрений, достигая твердой поверхности, «прилипает» к ней частичками, которые соприкасаются споверхностью, при этом соседние слои продолжают свое движение. Более того, у них резко увеличивается скорость по мере удаления от поверхности. Данное поведение слоев и приводит к завихренности потока. Область, где образуется сильно завихренный слой активной среды, и называют пограничным слоем.
Для описания и расчета параметров течения используются уравнения Навье-Стокса для количества движения:

Дополнительно, необходимо использовать уравнение неразрывности, то есть уравнение сохранения массы, в раскрытом виде:

Общие уравнения Навье-Стокса могут быть применены для пограничного слоя благодаря его малому поперечному размеру (высоте).
Рассмотрим теперь схематическое изображение образования пограничного слоя, представленное на рис. 3. Выберем систему координат, связанную с твердым телом: ось Ох направим вдоль образующей тела, а ось Оу – по нормали к ней. Соответственно компонент скорости вдоль оси Ох – u, а вдоль оси Оу – v.

Рисунок 3. Картина образования пограничного слоя
Теперь, допустимо провести некоторую оценку членов, входящих в уравнения Навье-Стокса. Для нашего случая:

Здесь размерные параметры отмечены чертой. Можно заметить, что некоторые члены становятся весьма малыми по сравнению с другими, потому что число Рейнольдса ReL здесь достаточно велико. Такие члены можно отбросить. Врезультате приходим к системе уравнений, полученных Л. Прандтлем, для несжимаемой жидкости:
 (2.1) (2.1)
В данной системе давление Р является функцией только координаты х и времени t, следовательно, не зависит от координаты у, v – кинематическая вязкость газа. Если ввести функцию тока ψ, положив u = ∂ψ/∂y; v = -∂ψ/∂x, то мы получим уравнение для стационарного течения около пластины, где давление не зависит от координаты у и постоянно:
 (2.2) (2.2)
C такими граничными условиями:
 (2.3) (2.3)
В таком виде решение уравнения (2.2) весьма затруднительно.
П. Рихардом и Г. Блазиусом была предложена постановка задачи применительно к плоской пластине, дающая допустимое решение для всей пластины, за исключением передней и задней кромок, и позволяющая с достаточной точностью найти сопротивление пластины. Далее вместо пластины конечной длины L он рассмотрел полубесконечную пластину с передней кромкой в начале координат. Отсутствие в граничных условиях длины L позволило привести уравнение вчастных производных к автомодельному виду, т.е. к уравнению с одной переменной с помощью преобразования:
 (2.4) (2.4)
с граничными условиями: f = 0, f' = 0 при η = 0, f' → 1 при η → ∞.
Г. Блазиус получил решение этого уравнения путём сопряжения двух рядов при малых и больших значениях η. В дальнейшем К. Тёпфер, Л. Хоуарт и Хартри получили решение этого уравнения численным методом с большей точностью. Сравнивая полученные результаты с экспериментальными данными, получаем реальное подтверждение результатов.
В случае сжимаемого газа (ρ = ρ(η)) уравнение Г. Блазиуса (2.2) принимает вид:
 (2.5) (2.5)
где

При этом граничные условия принимают вид: f = 0, f' = 0, g = gw при η = 0, f' → 1, g → 1 при η → ∞.
Коэффициент трения и толщины пограничного слоя можно вывести из соотношений:
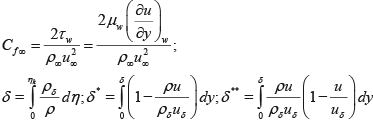 (2.6) (2.6)
В итоге для расчета параметров турбулентного пограничного слоя используются двухслойные модели Л. Прантля и Клаузера-Клебанова.
Главной целью является построение и реализация программы для корректировки расчета параметров пограничного слоя с учетом влияния градиента давления и пульсации внешнего потока.
На текущий момент аналогов ПО для нахождения конкретных точек перехода с учетом градиента давления не так много.
Одним из самых ярких представителей, похожих по смыслу, является программа для моделирования полета в аэродинамической трубе QBlade.

Рисунок 4. Пример расчета в программе QBlade
Данную программу можно использовать в общем случае изучения явлений и процессов, происходящим над/с телом в состоянии обдувания. Но она не подходит для изучения влияния градиента давления, т.к. не позволяет задать определенный алгоритм корректировки и удобно работать с входными данными (в режиме командной строки), отлаживать вычисления. К несомненным плюсам можно отнести бесплатность и кроссплатформенность (написана сиспользованием Qt).
Другим аналогом могут выступать собственные вычисления в среде Matlab/Simulink с помощью различных ToolBox. На сегодняшний день для подобной задачи доступен Aerospace Toolbox. «Aerospace Toolbox предоставляет эталонные стандарты, модели окружающей среды и импортирование аэродинамических коэффициентов для проведения расширенного аэрокосмического анализа для разработки и оценки ваших проектов. Варианты визуализации динамики воздушного объекта включают в себя анимации MATLAB® с шестью степенями свободы и интерфейсы к симулятору полета FlightGear, программному обеспечению Simulink 3D Animation™. Эти параметры позволяют визуализировать данные полета в трехмерной (трехмерной) среде и восстанавливать поведенческие аномалии в результатах летных испытаний», – гласит описание ToolBox на сайте MatLab.
Данный вариант действительно хорош, поскольку для расчетов будет использовано ядро Matlab, а оно успело себя хорошо зарекомендовать. Но есть один существенный недостаток: для запуска таких программ будет необходим сам установленный Matlab, т.е нельзя использовать его на каждой платформе. И хотя есть специальный ToolBox для перевода программы расчета с языка Matlab на язык С++, такой способ имеет свои ограничения и подразумевает знание двух языков программирования вместо одного, что повышает входной уровень для разработки и поддержки данной программы. Более того, данный математический пакет не является бесплатным и свободно распространяемым, что тоже можно считать в целом отрицательным моментом.
Для реализации поставленной задачи были написаны программы на языках высокого уровня (C++ и C#), которые производят вычисления по представленному ниже математическому алгоритму и позволяют удобно с ними работать.
Поскольку уравнения пограничного слоя являются нелинейными уравнениями, то необходимо применить метод квазилинеаризации. Одним из основных методов математического аппарата, который используется в данной работе, является метод квазилинеаризации. Если необходимо определить начальные условия на остром конусе, то решаются обобщенные уравнения Г. Блазиуса:

с граничными условиями:
при η = 0, f = fw, f' = 0,..., g = gw; при η → ∞, f' → 1, g → 1 (3.1)
Для наконечника с оживальным притуплением небольшую окрестность носка тела можно рассматривать как острый конус и по нему найти начальные условия.
Здесь рассматривается расчет начальных профилей функции тока f и энтальпии g на примере решения уравнения Г. Блазиуса, полагая для простоты число Прандтля Pr = 1 и коэффициент вязкости μ ≈ СТ, следовательно, N = 1, P = 1, Q = 0:
 (3.2) (3.2)
Применяя метод квазилинеаризации к системе уравнений (3.2), получим:

Здесь (k)f, (k)g – предыдущие приближения, а (k+1)f, (k+1)g – искомые приближения. Предполагая, что (k)f, (k)g удовлетворяют системе (3.2) и краевым условиям (3.1), получается:
 (3.3) (3.3)
Краевая задача, описываемая системой (3.1), (3.3), решается методом скалярной прогонки. Обнаруженные профили безразмерной функции тока, функции скорости и полной энтальпии записываются в предшествующие два сечения по s идалее отыскиваются решения при новоиспеченной величине s.
При этом течение в переходном слое стремительно возобновляется при увеличении координаты s. Нахождение поведения параметра g можно осуществить точно так же, как и нахождение функции f (функции тока).
Заранее следует оговорить основные предположения, которые используются при выводе уравнений пограничного слоя:
- число Рейнольдса ReL∞ >> 1;
- толщина пограничного слоя δ/L << 1;
- толщина слоя мала по сравнению с радиусами продольной и поперечной кривизны поверхности тела.
Уравнения двумерного стационарного пограничного слоя имеют вид:
 (3.4) (3.4)
- уравнение сохранения количества движения
 (3.5) (3.5)
- уравнение сохранения энергии
 (3.6) (3.6)
Линейные параметры, такие как s, n, r, относятся к протяженности тела L. Переменные скорости u, v относятся к скорости набегающей струи V∞. Такие газодинамические параметры, как ρ, p, J, μ, ε, соответственно относятся к ρ∞, ρ∞V∞2, V∞2, μ∞, μδ/ρδ. Молекулярное число Прандтля Pr и турбулентное Prt предполагаются постоянными величинами. γt – коэффициент перехода от ламинарного (γt = 0) течения к турбулентному (γt = 1).
В связи с тем, что систему уравнений необходимо замкнуть, требуется добавление физических законов изменения для τ и ρ в зависимости от р и h. В статье указано произведение ρ и µ в следующем виде:

Важно отметить, что при выводе этой формулы использовалась степенная зависимость μ ~ СТn, которой удобно пользоваться равно как для совершенного газа, так и для равновесно-диссоциированного воздуха. Тем не менее в некоторых случаях можно применять формулу Сатерленда:

где для воздуха Ts = 375K; значения µo, To соответствуют начальному состоянию газа (например, To = 273К, µo = 1,754∙10-5 Па∙с).
Уравнение состояния используется в двух формах, но нас интересует форма для совершенного газа:
p = ρRT, R = 287 Дж/(К∙моль) (воздух)
Коэффициент перехода от ламинарного течения к турбулентному γt определяется из выражения:
 (3.7) (3.7)
Здесь sнп и Resнп – координата точки и число Рейнольдса начала перехода. Предложенная ранее формулировка позволяет знать лишь координаты точки, в которой происходит начало перехода, – sнп, вторая координата, т.е координата окончания перехода sкп будет определена самостоятельно. Формула (3.7) предусматривает влияние числа Мδ на площадь переходной зоны – с увеличением Мδ площадь зоны перехода возрастает. При умеренных числах М область перехода в процентном соотношении занимает приблизительно ту же часть, что и ламинарная.
Влияние градиента давления определяется интегральным соотношением в выражении (3.7), которое учитывает изменение скорости на внешней границе пограничного слоя uδ(s).
Внешняя часть пограничного слоя здесь будет рассмотрена как слой смешения при взаимодействии двух потоков, при этом турбулентная кинематическая вязкость εo рассчитывается по модели Клаузера-Клебанова. Согласно модели кинематическая вязкость принимается постоянной в поперечном сечении пограничного слоя, а также пропорциональной характерному размеру пограничного слоя, т.е. толщине вытеснения δ*, и среднему значению дефекта скорости:

Для учета процессов перемежаемости вблизи внешней границы слоя смешения вводят экспериментально определенный Клебановым эмпирический коэффициент перемежаемости:

Следовательно, кинематический коэффициент турбулентной вязкости во внешней части слоя имеет вид:
 (3.8) (3.8)
Условием перехода от одного значения турбулентной вязкости к другому служит равенство εi = εo. Таким образом, полностью сформулирована задача для определения параметров течения в турбулентном пограничном слое.
Следует также отметить, что интегрирование уравнений пограничного слоя, записанных в форме (3.4)-(3.6), не представляется тривиальной задачей, поскольку при увеличении координаты s толщина слоя δ и верхняя граница области всевремя будут возрастать, причем по различным законам для ламинарного и турбулентного слоя. Имеет смысл использовать переменные, у которых верхняя граница была бы постоянной на протяжении всей площади течения.
Подобные переменные предложены в труде и выглядят следующим образом:
 (3.9) (3.9)
Здесь параметр γ1 = 2 для ламинарного слоя и γ1 = 1.25 для турбулентного слоя. В этих переменных конечная координата интегрирования ηk не превышает 7.0 для ламинарного течения и 0.7 – для турбулентного. Поэтому при решении поставленной подзадачи в качестве конечной координаты принимались именно эти значения.
Система уравнений (3.4)-(3.6) при переходе к новым переменным будут выглядеть следующим образом:

где ψ, f – размерная и безразмерная функция тока; g – отношение полных энтальпий в пограничном слое и внешнем потоке, имеет вид:
 (3.10) (3.10)
 (3.11) (3.11)
Здесь:

Коэффициенты турбулентной вязкости преобразуются к следующему виду:
а) Во внутренней области:

-84-92-web-resources/image/Formula_29.png) Для случая потока без массообмена: Для случая потока без массообмена:

а с массообменом:
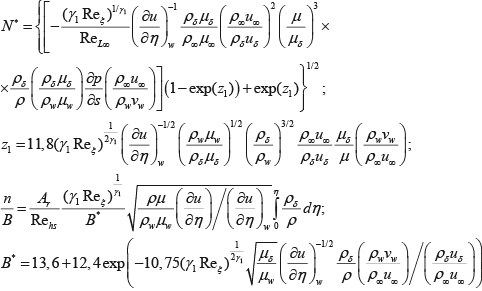
б) Во внешней области:

Краевая задача для нелинейных ДУ (3.10, 3.11) решается при помощи квазилинеаризации. Сущность этого метода состоит в том, что над уравнениями производится процесс линеаризации относительно известного приближенного решения, и полученные линейные уравнения решаются так, чтобы решение удовлетворяло бы всем граничным условиям.
Рассмотрим пример, который имеет общий вид L(y'', y', y) = 0. При использовании метода квазилинеаризации получаем следующее:

В случае (k)y = (k+1)y квазилинеаризированное уравнение превращается в точное. Однако данный метод не допускает возможность получить 0-приближение. При использовании аппарата квазилинеаризации мы имеем возможность достигнуть квадратичной сходимости поочередных приближений и монотонной сходимости к правильному решению.
Входящие в систему уравнений функции N, P, Q зависят от многих переменных, например:

поэтому формальное использование метода квазилинеаризации привело бы к весьма громоздким выражениям. Удобнее предположить, что N, P и Q определяются по параметрам g, f' и т.д., найденным из предыдущего приближения. Тогда применение метода квазилинеаризации к системе уравнений (3.10, 3.11) приводит их к виду:
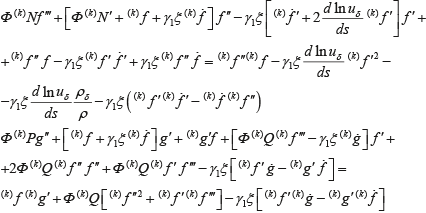 (3.12) (3.12)
Граничные и начальные условия (3.1) при этом полностью сохранятся. Условия при η → ∞ можно отнести на конечное значение ηk = 7 для ламинарного слоя и на ηk = 0.7 для турбулентного слоя при простых (f = f' = 0; g = gw) условиях настенке. В том случае, если присутствуют расходимости итераций любых решений, значения ηk можно повысить.
Процедура нахождения решения заключается в том, что сперва формируются на новоиспеченном s внешние характеристики и условия на стенке, а далее отыскивается новая величина ξ и решается система (3.12) при помощи методики последовательного приближения. Всякий раз при получении нового s за 0-приближение функций подставляются те же функции (o)f, (o)f', (o)f'', (o)g, (o)g' которые были получены на прошлом шаге по s. Многочисленные расчеты показали, что в большинстве случаев требуется 2-3 последовательных приближения, а при положительном градиенте давления 3-4 приближения. Производные ḟ, ż, ġ, заменяются интерполяционными полиномами Лагранжа по трем слоям s со вторым порядком точности:

Следует заметить, что в этом случае профили скорости и энтальпии сильнее всего изменяются вблизи стенки и незначительно в районе внешней границы пограничного слоя. Поэтому шаг интегрирования по координате η в поперечном направлении необходимо сделать переменным: малым вблизи стенки, поскольку в турбулентном слое коэффициент трения должен быть соответствующим ламинарному подслою и составлять ~ 0.0005 ÷ 0.001 от толщины слоя, и большим вблизи ηk.
В расчетах шаг по координате ηk изменялся по геометрической прогрессии hn = hokn-1; k = 1.120125, причем для ламинарного слоя ho = 10-5, а для турбулентного – ho = 10-6. Число шагов по координате η обычно составляло 100.
В этом случае выражения для третьей, второй и первой производных по координате η имеют соответственно вид:



Подставляя конечно-разностные выражения производных в систему (3.12), приходим к следующему выражению:

где


Затем необходимо определить выражения для прогоночных коэффициентов:

Начальные условия на стенке необходимы для определения первых прогоночных коэффициентов:

По этим коэффициентам легко определяются и остальные коэффициенты Аn, Bn, Cn от n = 3 до точки N-2.
На внешней границе пограничного слоя выполняется условие: f' = 1; η = ηk. Однако для определения функции тока fN и fN-1 в точках ηk и ηk–hN одного этого условия недостаточно. Необходимо добавить равенство f''(ηk) = 0, которое вытекает из асимптотического характера поведения функции f' на границе пограничного слоя: f' → 1 при η → ηk.
Используя конечно-разностные представления для уравнений f'(ηk) = 1, f''(ηk) = 0 и дополняя их прогоночными соотношениями в точках N-2 и N-3, получаем систему уравнений:

относительно неизвестных fN, fN-1, fN-2, fN-3. Определяя fN и fN-1 из данной системы, находим с помощью обратного хода значения функции тока fi во всех остальных точках.
Уравнение энергии (3.3) также решается методом прогонки. Используя конечно-разностное представление производных функции g, запишем его в виде:

где

Параметр gn можно представить в виде:

где:

Из начального условия при η = 0 находятся первые прогоночные коэффициенты: D1 = 0; E1 = 0; N1* = gw, по которым определяются все остальные вплоть до точки N-2. При условиях g(ηk) = 1 и g'(ηk) = 0, а вдобавок прогоночное соотношение в N-2, возможно получить систему уравнений для того, чтобы определить функции gN-1. И лишь найдя gN-1 при помощи обратного хода можно будет определить функции gi в любых точках.
Решение считается найденным, если:

Если эти условия не выполняются, то итерационный процесс повторяется. Обычно εf = 10-4, εg = 5∙10-4. Несколько уменьшенная точность в εg связана с наличием диссипативного члена [ФQf'f''], расчет которого осуществляется с большой погрешностью.
После того как профили f и g были найдены с установленной точностью, необходимо найти параметры в сечении согласно положению s.
Важно отметить, что в данной работе рассматривается преимущественно 2D-картина, т.е. не учитываются никакие силы по оси Z.
Корректировка числа Рейнольдса в программе осуществляется с помощью алгоритма, предложенного в статье. Изложенные там выводы были основаны на фактических экспериментах, и полученные числа подтверждаются другими многочисленными экспериментами.
Параметр градиента давления λθ вычисляется так:
 (3.13) (3.13)
Параметр ускорение потока K можно найти, используя следующую формулу:
 (3.14) (3.14)
Параметр dU/ds является ускорением вдоль направления потока и может быть вычислен нахождением производной скорости в направлениях x и y, затем необходимо сложить следующим образом:
 (3.15) (3.15)
 (3.16) (3.16)
 (3.17) (3.17)
 (3.18) (3.18)
Для расчета итоговой корректировки необходимо использовать следующую формулу:
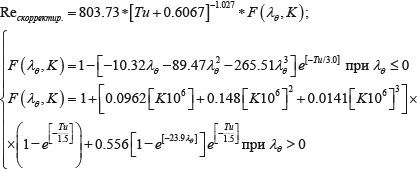 (3.19) (3.19)
где Tu – локальная интенсивность турбулентности, выраженная в процентах. Для численной устойчивости параметры ускорения и эмпирическая корреляция должны быть ограничены следующим образом:
–0.1 ≤ λθ ≤ 0.1 (3.20)
–3×10-6 ≤ K ≤ 3×10-6 (3.21)
Reскорректир. ≥ 20 (3.22)
Значения 3.20-3.22 для программы будут задаваться пользователем вручную, так как это необходимые для каждой конкретной ситуации параметры и быть автоматически рассчитанными они не могут.
Итоговая программа состоит из двух логических модулей: ядро вычислений и GUI (графический интерфейс для визуализации результатов).
Ядро представляет собой логически законченную программу. В нем запрограммирована вся логика описанная выше. На вход программе подается специальным образом сконфигурированный .ini файл.

Рисунок 5. Пример конфигурационного ini-файла для ядра
Используя данные, которые заданы в ini-файле, программа производит расчет необходимых величин и в зависимости от настроенного вывода может передавать данные в GUI или файл отчета в различных форматах.

Рисунок 6. Пример файла вывода расчетов ядра
GUI представляет собой графическую оболочку над ядром и служит инструментом манипуляции и визуализации полученных данных от ядра. Программа реализована на C# с использование WinForms.

Рисунок 7. Пример построения линии по точкам из расчетов ядра
Визуализация происходит средством нанесения полученных точек на график, тем самым для конечного пользователя удобно визуально оценивать полученные расчеты, сохранить полученный график. Под манипуляцией подразумевается возможность в дальнейшем удобно хранить и сортировать полученные данные.
Таким образом, в зависимости от полученных данных от ядра можно получить визуализацию различных ситуаций и смоделировать поведение характеристик при различных начальных условиях.
После успешной реализации программы и проведения различных проверок были окончательно получены подтверждения тому факту, что полученные в ходе вычисления программой данные соответствуют многочисленным экспериментам.
Ключевые слова: ламинарное течение, турбулентное течение, градиент, уравнения Навье-Стокса, пограничный слой, пульсация внешнего потока, метод квазилинеаризации, краевая задача, визуализация, C#, C++, WinForms, числа Маха, числа Рейнольдса.
A program complex for solving equations of a two-dimensional boundary layer
Sobenevsky A.P., Moscow Aviation Institute (National Research University), 812-th department, technician
Povalyaev P.P., Moscow Aviation Institute (National Research University), 812-th Department, engineer
Abstract: This article describes the developed program in C ++ & C # languages to solve the equations of a two-dimensional boundary layer on the surface of an aircraft at supersonic flight speeds based on quasilinearization and scalar sweep methods. This program allows you to find both local and integral parameters of the laminar, transition and turbulent boundary layer. These parameters are necessary for determining the components of aerodynamic characteristics of aircraft with regard to viscous effects. As a result, a calculation program (core) and a graphical program (GUI) were received to receive and process the data. In addition, the work presented a comparison of the result of the program with real experimental data. This software can be used in various companies that specialize in the manufacture of parts. Moreover, on almost any platform, regardless of the level of obsolescence of computers in the enterprise. Together, this makes the PC not only unique, but also relevant for enterprises in the relevant areas of work.
Keywords: laminar flow, turbulent flow, gradient, Navier-Stokes equations, boundary layer, external flow pulsation, quasi-linearization method, boundary value problem, visualization, C #, C ++, WinForms, Mach numbers, Reynolds number.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
