ТЕПЛОВ А.А., магистр, МГТУ имени Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии», Москва, teploff.aa@gmail.com

 МАЙКОВ К.А., д.т.н., профессор, МГТУ имени Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии», Москва, maikov@bmstu.ru

Экспериментальные исследования
алгоритма синтеза трехмерных фрактальных динамических структур

Разработан алгоритм, преимущественной особенностью которого являются применимость к синтезу трехмерных фрактальных динамических структур, обеспечение приемлемой масштабной инвариантности, а также его высокое быстродействие и низкая ресурсоемкость. Анализ результатов машинных экспериментов подтвердил практическую применимость предложенного алгоритма для формирования трехмерных фрактальных объектов виртуальной реальности

Введение

Большинство объектов реального мира характеризуется нерегулярностью структуры, что затрудняет практическое применение заранее выбранных моделей классической геометрии для их представления. Поэтому решение проблемы формирования таких объектов в условиях совмещенной реальности приобретает неоспоримую практическую актуальность.

Примерами таких объектов являются структуры земной и водной поверхности, растительный покров, сердечно-сосудистая система человека и т.д.

Весьма перспективным решением поставленной проблемы является применение математического аппарата фракталов [4]. Однако, как показано в [6], существуют решения, применимые лишь для синтеза простейших двумерных структур.

В связи с вышеизложенным необходимо разработать метод, который бы отвечал требованиям формирования трехмерных фрактальных объектов с приемлемой степенью детализации структуры.

Алгоритм формирования трехмерных фрактальных динамических структур

Схема алгоритма формирования трехмерных фрактальных динамических структур [6] представлена на рис. 1. Так как алгоритм представляет собой функциональное единство алгоритмов формирования двоичного дерева и кривой «дракона» [6], то именно они определяют ресурсоемкость и представляют собой практический интерес в представленной схеме.

Как уже было сказано выше, алгоритм декомпозируется на два основных этапа, представленные на рис. 1 блоками «А» и «Б» соответственно.

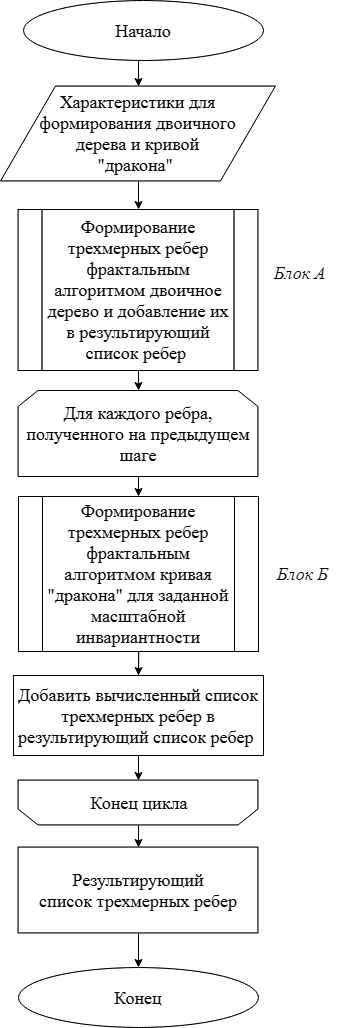
Рисунок 1. Схема алгоритма формирования трехмерных фрактальных динамических структур

Блок «А» представляет собой отдельный этап, отвечающий за формирование трехмерной древовидной структуры фрактальным алгоритмом двоичное дерево [6], и главной отличительной чертой которого является представление результирующей структуры в виде иерархической системы. Схема алгоритма формирования трехмерной древовидной структуры представлена на рис. 2.

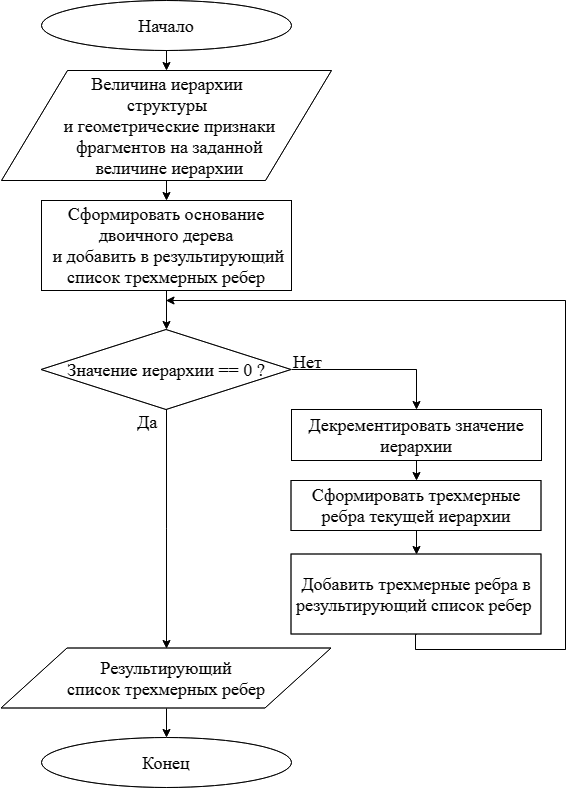
Рисунок 2. Схема алгоритма формирования трехмерной древовидной структуры

Формирование трехмерной структуры, обеспечивающее заданную степень детализации отдельного фрактального фрагмента, представлено блоком «Б» на рис. 1. При помощи алгоритма кривая «дракона» [6] осуществляется необходимая масштабная инвариантность, описывающая все многообразие и сложность отдельно рассматриваемой структуры. Схема алгоритма формирования трехмерной структуры с заданной масштабной инвариантностью представлена на рис. 3.

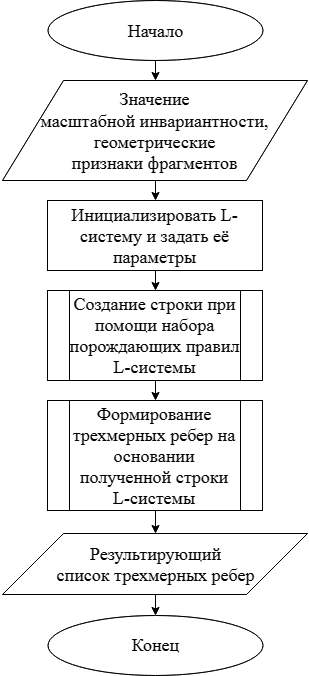
Рисунок 3. Схема алгоритма формирования трехмерной структуры с заданной масштабной инвариантностью

Алгоритм формирования трехмерной древовидной структуры

Как было сказано в [7], алгоритму присущ иерархический и рекурсивный характеры, что вытекает из главного фрактального свойства – самоподобия [2]. Главными свойствами данного алгоритма, схема которого представлена на рис. 2, являются величина иерархии структуры и геометрические признаки фрагментов на заданной величине иерархии.

Геометрические признаки определяются условиями поставленной задачи. Например, в случае формирования кровеносной системы человека ими могут быть:

• длина артериальной, венозной или капиллярной системы;
• диаметр отдельно взятого сосуда;
• пропускная способность артерии и прочее.

Результатом работы алгоритма является список трехмерных ребер, который в дальнейшем подвергается формированию, удовлетворяющему заданной степени детализации.

Алгоритм формирования трехмерной структуры с заданной масштабной инвариантностью

Как и предыдущий алгоритм, алгоритм формирования трехмерной структуры с заданной масштабной инвариантностью, представленный на рис. 3, по своему характеру рекурсивен [5]. Главной отличительной особенностью указанного алгоритма является представление структуры с заданной степенью детализации. Подобные фракталам формы с необходимой степенью детализации легко описать с помощью L-системы [14], так как рекурсивная природа правил L-системы приводит к самоподобию. L-система определяется как кортеж вида [9]:

G = (V, ω, P)

где:

• V (алфавит) – это множество символов, содержащих как элементы, которые могут быть заменены (переменные), так и элементы, которые не могут быть заменены (константы или терминальные символы) [9];
• ω (старт, аксиома или инициатор) – это строка символов из V, определяющая начальное состояние системы [9];
• P – это множество порождающих правил, определяющих, каким образом переменные могут быть заменены комбинациями констант и других переменных. Порождающее правило состоит из двух строк – прототип и преемник. Для любого символа A, входящего в алфавит V, не входящего в левую часть правил P, предполагается правило вывода A → A. Эти символы называются константами или терминальными символами [9].

Результатом работы L-системы будет являться результирующая строка, на основании которой необходимо сформировать трехмерные ребра. Чем выше степень детализации структуры, тем больше результирующая строка L-системы.

Экспериментальные исследования

Исследования проводились на аппаратной платформе со следующими характеристиками:

• процессор – четырехъядерный Intel i5 3.2Ghz;
• оперативная память – 16 Gb;
• операционная система – CentOS 7 [8].

Программная реализация алгоритма выполнена на языке программирования Python третьей версии [12] при помощи развитых интегрируемых библиотек, таких как:

• matplotlib [10],
• numpy [11],
• scipy [13],
• turtle [15],

предназначенных для осуществления научных и инженерных расчетов с последующей визуализацией результатов.

Входные данные для экспериментальных исследований представлены последовательностью значений от 1 до 30 единиц величин иерархии структуры и от 1 до 20 единиц значений масштабной инвариантности, что определяется особенностью отображения трехмерной системы с практически приемлемой степенью детализации [4].

Экспериментальные исследования представляли собой серию из ста реализаций вычислительных экспериментов для каждого из вышеуказанного значения диапазона.

Полученные результаты численных экспериментов были подвергнуты дальнейшей обработке в целях выявления достоверности временной зависимости. Для этого применен следующий набор вычислений:

1. Вычисление среднего значения измерительной величины согласно формуле (1):

(1)

где:

• x₁ + x₂ + ... + x_n – значения временных характеристик эксперимента;
• n – количество временных характеристик эксперимента.

2. Определение значения стандартного отклонения результатов, характеризующее разброс относительно среднего значения, согласно формуле (2):

(2)

3. Исключение величин, отклонение которых от среднего значения превышает утроенное стандартное отклонение, согласно [3].

Исследование зависимости времени формирования трехмерной древовидной структуры фрактальным алгоритмом двоичное дерево от значения величины иерархии

Обработанные полученные результаты проведенных экспериментальных исследований зависимости времени формирования трехмерной древовидной структуры фрактальным алгоритмом двоичное дерево от значения величины иерархии представлены на рис. 4.

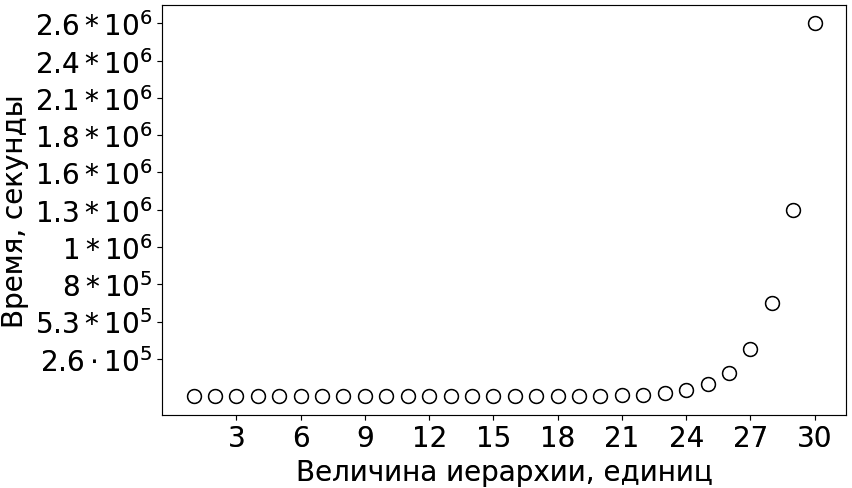
Рисунок 4. Зависимость времени формирования трехмерной древовидной структуры фрактальным алгоритмом двоичное дерево от значения величины иерархии

Поскольку задача формирования трехмерных древовидных структур в режиме реального времени характеризуется временными значениями, не превышающими двух секунд [4], то особый интерес представляют результаты, удовлетворяющие данному временному значению.

На рис. 5 представлена зависимость времени формирования трехмерной древовидной структуры фрактальным алгоритмом двоичное дерево от значения величины иерархии в диапазоне времени до двух секунд.

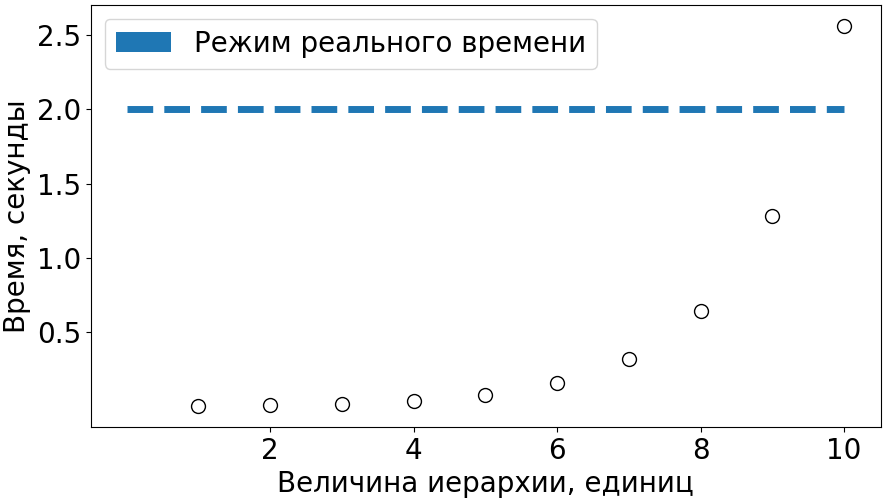
Рисунок 5. Зависимость времени формирования трехмерной древовидной структуры фрактальным алгоритмом двоичное дерево от значения величины иерархии в диапазоне времени до двух секунд

Из представленной на рис. 5 зависимости видно, что при величине иерархии, не превышающей значение девять единиц, алгоритм удовлетворяет указанным выше требованиям.

Исследование зависимости времени формирования трехмерной структуры фрактальным алгоритмом кривая «дракона» от значения масштабной инвариантности

Обработанные результаты проведенных экспериментальных исследований зависимости времени формирования трехмерной структуры фрактальным алгоритмом кривая «дракона» от значения масштабной инвариантности представлены на рис. 6.

Рисунок 6. Зависимость времени формирования трехмерной структуры фрактальным алгоритмом кривая «дракона» от значения масштабной инвариантности

Задача вычисления трехмерных структур с заданной масштабной инвариантностью в режиме реального времени также характеризуется временными значениями, не превышающими двух секунд [4].

Следовательно, особый практический интерес возникает к результатам, время вычисления которых удовлетворяет данному временному интервалу.

Из представленной на рис. 7 зависимости видно, что при масштабной инвариантности не более восьми единиц алгоритм удовлетворяет вышеуказанному условию.

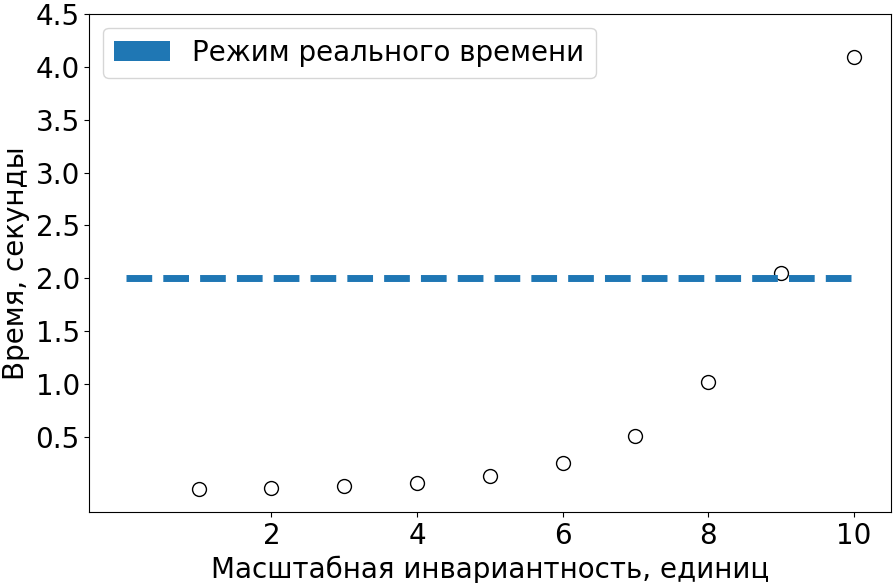
Рисунок 7. Зависимость времени формирования трехмерной структуры фрактальным алгоритмом кривая «дракона» от значения масштабной инвариантности в диапазоне времени до двух секунд

При увеличении значений величины иерархии и величины масштабной инвариантности более чем на девять и восемь единиц соответственно возникает необходимость дальнейшего развития предложенного алгоритма.

Одним из путей развития является применение технологий параллельных вычислений. Реализация такого технологического развития алгоритма определяет необходимость применения иных платформ программной разработки, использующих C-подобные [1] языки программирования.

Выводы

Проведенные численные экспериментальные исследования алгоритма синтеза трехмерных фрактальных динамических структур подтвердили работоспособность разработанных алгоритмических структур и их практически приемлемую ресурсоемкость.

Анализ результатов численных экспериментов показал, что для величины иерархии и величины масштабной инвариантности, не превышающих девяти и восьми единиц соответственно, алгоритм удовлетворяет требованиям реального времени. Предложено дальнейшее направление развития алгоритма путем внедрения многопоточного подхода вычисления.

1. Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. – Издательский дом «Вильямс». – 2001.
2. Балханов В.К. Основы фрактальной геометрии и фрактального исчисления/ от. ред. Башкуев Ю.Б. – Улан-Удэ: Изд-во Бурятского госуниверситета, 2013. – 224 с.
3. Косарев Е.Л. Методы обработки экспериментальных данных. – М.: ФИЗМАТЛИТ, 2008. – 210 с.
4. Мандельброт Б. Фрактальная геометрия природы. – Москва: Институт компьютерных исследований, 2002. – 656 с.
5. Морозов А.Д. Введение в теорию фракталов. – Москва-Ижевск: Институт компьютерных исследований, 2002. – 160 с.
6. Теплов А.А., Майков К.А. Анализ алгоритмов вычисления геометрических фракталов применительно к синтезу трехмерных динамических древовидных структур. // «Системный администратор», № 4, 2018 г. – С. 87-93.
7. Федер Е. Фракталы: Пер. с анг. – М.: Мир, 1991. – 254 с.
8. СentOS. [Электронный ресурс]. Режим доступа: https://www.centos.org/ (дата обращения 10.04.2018).
9. L-система. [Электронный ресурс]. Режим доступа: https://ru.wikipedia.org/wiki/L-система (дата обращения 10.04.2018).
10. Mathplotlib. [Электронный ресурс]. Режим доступа: https://matplotlib.org/ (дата обращения 10.04.2018).
11. NumPy. [Электронный ресурс]. Режим доступа: http://www.numpy.org/ (дата обращения 10.04.2018).
12. Python 3.0. [Электронный ресурс]. Режим доступа: https://www.python.org/ (дата обращения 10.04.2018).
13. SciPy. [Электронный ресурс]. Режим доступа: https://www.scipy.org/ (дата обращения 10.04.2018).
14. Stelios Manousakis. Musical L-Systems. – The Hague: The Royal Conservatory, 2006. – 133 p.
15. Turtle. [Электронный ресурс]. Режим доступа: https://docs.python.org/3/library/turtle.html (дата обращения 10.04.2018).

Ключевые слова: трехмерные фракталы, виртуальная реальность, построение динамических трехмерных фрактальных объектов.

Experimental researches of the algorithm applied to the synthesis of three-dimensional, fractal and dynamic structures

Teplov A.A., Master, MSTU Bauman, Department of “Software Information Technologies”, Moscow, teploff.aa@gmail.com

Maikov K.A., Doctor of Technical Sciences, Professor, MSTU Bauman, Department of “Software and Information Technologies”, Moscow, maikov@bmstu.ru

Abstract: An algorithm is developed, the main features of which are the applicability to the synthesis of a three-dimensional fractal dynamic structures, the ensuring an acceptable scale invariance, high performance and low resource consumption. The practical significance and expediency of applying the algorithm for modeling three-dimensional fractal virtual reality objects have been confirmed with the computer experiments results.

Keywords: three-dimensional fractals, virtual reality, building of dynamic three-dimensional fractal objects.

Комментарии могут оставлять только зарегистрированные пользователи