|
Рубрика:
Наука и технологии
|
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
 ТЕПЛОВ А.А., магистр, МГТУ имени Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии», Москва, teploff.aa@gmail.com ТЕПЛОВ А.А., магистр, МГТУ имени Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии», Москва, teploff.aa@gmail.com
 МАЙКОВ К.А., д.т.н., профессор, МГТУ имени Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии», Москва, maikov@bmstu.ru МАЙКОВ К.А., д.т.н., профессор, МГТУ имени Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии», Москва, maikov@bmstu.ru
Анализ алгоритмов вычисления геометрических фракталов
применительно к синтезу трехмерных динамических древовидных структур
Приведены результаты сравнительного анализа практически востребованных алгоритмов построения двумерных фракталов, обладающих высоким быстродействием и низкой ресурсоемкостью. Обосновывается выбор прототипа дляпоследующей модернизации применительно к построению трехмерных динамических древовидных объектов с практически необходимой степенью детализации
В настоящее время в технологии совмещенной реальности существует проблема формирования объектов реального мира, отличающихся нерегулярностью структуры и ресурсоемкостью вычислений. Примерами таких объектов являются структуры земной и водной поверхности, растительный покров, сердечно-сосудистая система человека и т.д. Очевидно, что применение методов и объектов классической геометрии для формирования упомянутых объектов является трудоемким и порой нереализуемым [6]. Предложенная в [3] фрактальная теория принципиально способна справиться с поставленной проблемой, однако методы ее реализации представляют собой трудоемкий процесс и доведены до стадии практической применимости лишь для синтеза простейших двумерных структур. Поэтому в практике решения задач совмещенной реальности возникает необходимость определения прототипа метода формирования динамических трехмерных фрактальных структур, обладающего практически приемлемыми быстродействием и ресурсоемкостью.
Алгоритмы построения геометрических фракталов
Известные и практически востребованные алгоритмы геометрических фракталов можно классифицировать с точки зрения древовидности структуры. К классу древовидных алгоритмов могут быть отнесены следующие алгоритмы:
- множество Кантора [4];
- Пифагорово дерево [2];
- двоичное дерево [3].
К классу недревовидных алгоритмов построения геометрических фракталов можно отнести такие алгоритмы, как:
- кривая Коха [4];
- кривая «дракона» [3];
- кривая Гильберта [6].
- кривая Минковского [3];
- «салфетка» Серпинского [6];
- «ковер» Серпинского [6];
- «кладбище» Серпинского [6].
Также классификация алгоритмов может быть проведена на основе ограниченности структуры. К классу алгоритмов ограниченной структуры, могут быть отнесены алгоритмы:
- множество Кантора;
- «кладбище» Серпинского;
- «салфетка» Серпинского;
- «ковер» Серпинского.
К классу алгоритмов неограниченной структуры могут быть отнесены следующие алгоритмы:
- Пифагорово дерево;
- двоичное дерево;
- кривая Коха;
- кривая «дракона»;
- кривая Гильберта;
- кривая Минковского.
Проведем анализ функциональных и структурных особенностей основных алгоритмов формирования геометрических фракталов.
Метод вычисления алгоритмической сложности рекурсивных алгоритмов
Все перечисленные выше алгоритмы построения геометрических фракталов имеют рекурсивный характер, что вытекает из главного фрактального свойства – самоподобия [3]. Метод подстановки (итераций) [5] является широко используемым методом определения алгоритмической сложности рекурсивных алгоритмов и заключается в последовательной замене рекуррентной части в выражении для получения новых формализаций. Замена производится до тех пор, пока не будет достигнуто формализованное представление общего принципа в виде нерекуррентной формулы. После чего необходимо произвести доказательство полученной формулы методом математической индукции [5].
Метод математической индукции позволяет доказать истинность некоторого утверждения (Pn), который состоит из двух шагов:
- доказательство утверждения для одного или нескольких частных случаев P0, P1, ...;
- из истинности Pn (индуктивная гипотеза) и частных случаев выводится доказательство Pn+1.
Фрактальная размерность
Одной из важных характеристик фрактальной структуры является ее фрактальная размерность [1], показывающая, насколько плотно и равномерно элементы данного множества заполняют евклидово пространство (D < E). Фрактальная размерность определяется следующей формулой:
 (1) (1)
где Nε минимальное количество n-мерных окружностей радиуса ε, необходимых для покрытия множества.
Применим метод подстановки для анализа вышеупомянутых алгоритмов, а также вычислим фрактальную размерность для каждой из структур.
Анализ алгоритмов формирования геометрических фракталов
Рассмотрим известные алгоритмы формирования геометрических фракталов.
1. Кривая Коха
Процесс формирования геометрического фрактала кривой Коха выглядит следующим образом:
- отрезок единичной длины делится на три равные части;
- происходит замена среднего отрезка равносторонним треугольником;
- далее происходит повторение вышеописанных операций для каждого из четырех полученных отрезков и т.д.
Иллюстрация формирования геометрического фрактала кривой Коха первых четырех итераций представлена на рис. 1.
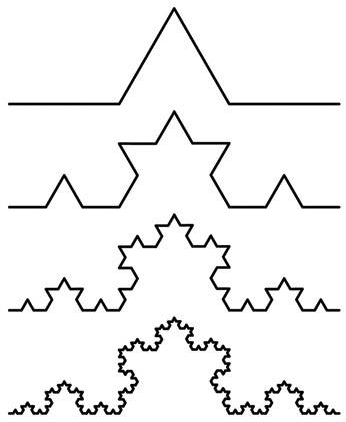
Рисунок 1. Формирование кривой Коха
Применяя метод подстановки и руководствуясь алгоритмом, изложенным выше, нетрудно определить зависимость времени формирования фрактальной структуры кривой Коха, а именно:
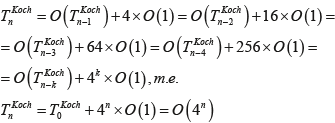 -87-93-web-resources/image/Formula_02.png)
Для доказательства истинности целесообразно применить метод математической индукции.
Докажем корректность предположения, сделанного при оценке трудоемкости алгоритма формирования кривой Коха,  : :
 верно из условия первоначальной подстановки; верно из условия первоначальной подстановки;
- допустим истинность
 ; ;
- требуется доказать, что
 ; ;
- сначала подставим n+1 в рекуррентное соотношение
 ; ;
- в правой части выражения можно произвести замену на основании индуктивной гипотезы:
  , что доказывает истинность первоначального предположения. , что доказывает истинность первоначального предположения.
Фрактальная размерность кривой Коха согласно формуле (1) приобретает следующий вид:

2. Кривая «дракона»
При формировании фрактальной структуры кривой «дракона» необходимо взять исходный отрезок, повернуть на 90 градусов вокруг одной из вершин и добавить полученный отрезок к первоначальному. Далее повернуть полученный угол на 90 градусов вокруг вершины и добавить полученную ломаную к исходной. Повторяя описанную процедуру, фрактальная структура приобретает все более сложный вид, напоминая дракона. Формирование описанной структуры показано на рис. 2.

Рисунок 2. Формирование кривой «дракона»
Анализ алгоритма формирования указанной структуры с использованием метода подстановки позволяет получить зависимость времени формирования кривой «дракона» в виде:
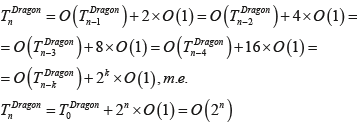 -87-93-web-resources/image/Formula_09.png)
Докажем корректность предположения, сделанного при оценке трудоемкости алгоритма формирования кривой «дракона»,  : :
 верно из условия первоначальной подстановки; верно из условия первоначальной подстановки;
- допустим истинность
 ; ;
- требуется доказать, что
 ; ;
- сначала подставим n+1 в рекуррентное соотношение:
 ; ;
- в правой части выражения можно произвести замену на основании индуктивной гипотезы:
  , что доказывает истинность первоначального предположения. , что доказывает истинность первоначального предположения.
Фрактальная размерность кривой «дракона» согласно формуле (1) приобретает следующий вид:

3. Кривая Гильберта
Для того чтобы сформировать фрактальную структура кривой Гильберта, необходимо иметь в распоряжении квадрат со стороной 0.5 единицы, убрать одну из его сторон и поместить построенную структуру в середину единичного квадрата. Результирующая структура имеет наименование «кривая Гильберта первого порядка».
Кривая второго порядка получается путем соединения прямыми линиями четырех кривых первого порядка. Аналогичным образом получается кривая третьего порядка и т.д.
Иллюстрация формирования кривых Гильберта от первого до шестого порядков соответственно представлена на рис. 3.
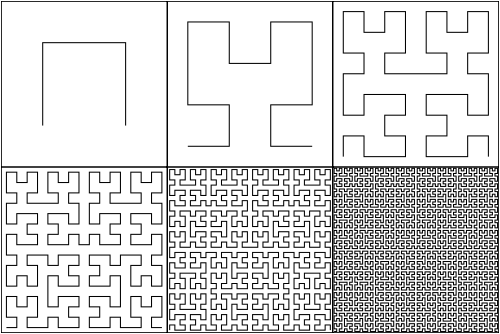
Рисунок 3. Формирование кривой Гильберта
Зависимость времени формирования фрактальной структуры кривой Гильберта выражается формулой:
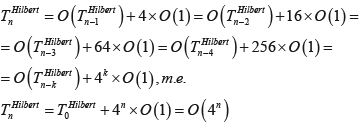 -87-93-web-resources/image/Formula_15.png)
Для доказательства истинности применим метод математической индукции.
Докажем корректность предположения, сделанного при оценке трудоемкости алгоритма формирования кривой Коха,  : :
 верно из условия первоначальной подстановки; верно из условия первоначальной подстановки;
- допустим истинность
 ; ;
- требуется доказать, что
 ; ;
- сначала подставим n+1 в рекуррентное соотношение:
 ; ;
- в правой части выражения можно произвести замену на основании индуктивной гипотезы:
  , что доказывает истинность первоначального предположения. , что доказывает истинность первоначального предположения.
Фрактальная размерность кривой Гильберта согласно формуле (1) приобретает следующий вид:

4. Кривая Минковского
Формирование кривой происходит следующим образом: отрезок единичной длины преобразуется в ломаную по исходному шаблону, часто называемому генератором. Исходный отрезок при помощи генератора делится на несколько составляющих, каждый из которого подвергается формированию по тому же шаблону, что и исходный и т.д. Формирование кривой Минковского представлено на рис. 4.
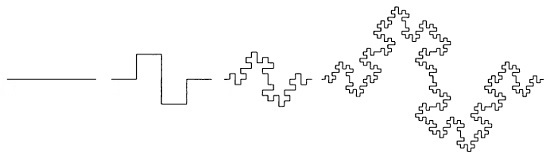
Рисунок 4. Формирование кривой Минковского
Зависимость времени формирования фрактальной структуры кривой Минковского представлена ниже:
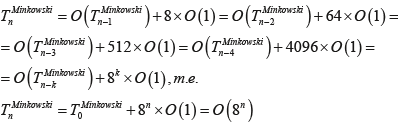 -87-93-web-resources/image/Formula_22.png)
Докажем корректность предположения, сделанного при оценке трудоемкости алгоритма формирования кривой «дракона»,  : :
 верно из условия первоначальной подстановки; верно из условия первоначальной подстановки;
- допустим истинность
 ; ;
- требуется доказать, что
 ; ;
- сначала подставим n+1 в рекуррентное соотношение:
 ; ;
- в правой части выражения можно произвести замену на основании индуктивной гипотезы:
  , что доказывает истинность первоначального предположения. , что доказывает истинность первоначального предположения.
Фрактальная размерность кривой Минковского согласно формуле (1) приобретает следующий вид:

5. Множество Кантора
При формировании множества Кантора за основу берется единичный отрезок, который подвергается формированию путем разметки его на три равные части и удалению средней части. Далее операция повторяется для двух других отрезков, полученных на предыдущем этапе, и т.д. Процесс формирования фрактальной структуры множества Кантора представлен на рис. 5.

Рисунок 5. Формирование множества Кантора
Зависимость времени формирования фрактальной структуры множества Кантора нетрудно получить в виде:
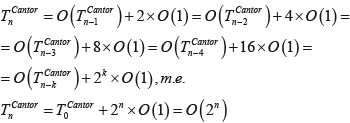 -87-93-web-resources/image/Formula_29.png)
Докажем корректность предположения, сделанного при оценке трудоемкости алгоритма формирования кривой «дракона»,  : :
 верно из условия первоначальной подстановки; верно из условия первоначальной подстановки;
- допустим истинность
 ; ;
- требуется доказать, что
 ; ;
- сначала подставим n+1 в рекуррентное соотношение:
 ; ;
- в правой части выражения можно произвести замену на основании индуктивной гипотезы:
  , что доказывает истинность первоначального предположения. , что доказывает истинность первоначального предположения.
Фрактальная размерность множества Кантора согласно формуле (1) приобретает следующий вид:

6. Пифагорово дерево
На рис. 6 [2] показаны первые восемь итераций 45-градусного Пифагорова дерева, которое формируется из трех квадратов, касающихся друг друга вершинами, образуя внутри прямоугольный треугольник с двумя углами по 45 градусов соответственно.
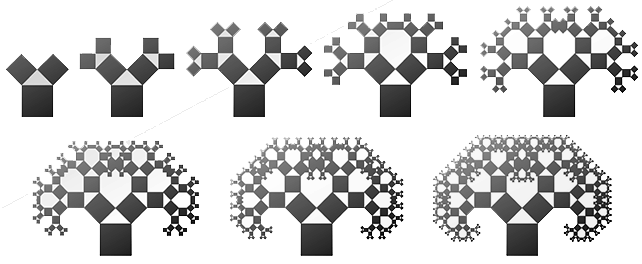
Рисунок 6. Формирование Пифагорова дерева
Зависимость времени формирования фрактальной структуры Пифагорова дерева представлена формулой вида:
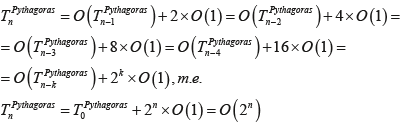 -87-93-web-resources/image/Formula_36.png)
Докажем корректность предположения, сделанного при оценке трудоемкости алгоритма формирования кривой «дракона»,  : :
 верно из условия первоначальной подстановки; верно из условия первоначальной подстановки;
- допустим истинность
 ; ;
- требуется доказать, что
 ; ;
- сначала подставим n+1 в рекуррентное соотношение:
 ; ;
- в правой части выражения можно произвести замену на основании индуктивной гипотезы:
  , что доказывает истинность первоначального предположения. , что доказывает истинность первоначального предположения.
Фрактальная размерность Пифагорова дерева согласно формуле (1) приобретает следующий вид:

7. Двоичное дерево
Фрактальная структура двоичного дерева, представленного на рис. 7, формируется по последующему принципу: вертикальный отрезок единичной длины конкатенируется с горизонтальным отрезком, который больше исходного в два раза, затем вертикальные отрезки с коэффициентом 0.5 от исходного конкатенируются с горизонтальным и т.д.
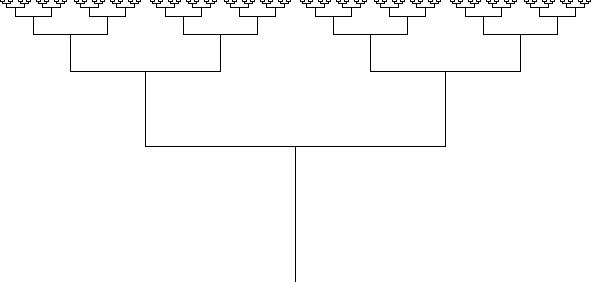
Рисунок 7. Формирование двоичного дерева
Временная зависимость формирования фрактальной структуры двоичного дерева представлена формулой вида:

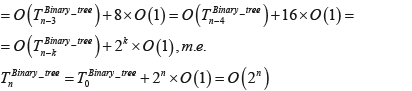 -87-93-web-resources/image/Formula_43.png)
Докажем корректность предположения, сделанного при оценке трудоемкости алгоритма формирования кривой «дракона»,  : :
 верно из условия первоначальной подстановки; верно из условия первоначальной подстановки;
- допустим истинность
 ; ;
- требуется доказать, что
 ; ;
- сначала подставим n+1 в рекуррентное соотношение:
 ; ;
- в правой части выражения можно произвести замену на основании индуктивной гипотезы:
  , что доказывает истинность первоначального предположения. , что доказывает истинность первоначального предположения.
Фрактальная размерность двоичного дерева согласно формуле (1) приобретает следующий вид:

8. «Салфетка» Серпинского
Формирование фрактальной структуры «салфетки» Серпинского происходит согласно следующему алгоритму: середины сторон исходного равностороннего треугольника соединяются отрезками. Получаются четыре новых треугольника. Изисходного треугольника удаляется внутренняя структура срединного треугольника. Получается множество, состоящее из трех оставшихся треугольников первого ранга. Поступая точно так же с каждым из треугольников первого ранга, получим следующее множество, состоящее из девяти равносторонних треугольников второго ранга и т.д. На рис. 8 представлены первые шесть итераций формирования фрактальной структуры.

Рисунок 8. Формирование «салфетки» Серпинского
Зависимость времени формирования фрактальной структуры «салфетки» Серпинского представлена ниже:
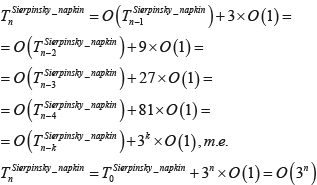 -87-93-web-resources/image/Formula_49.png)
Докажем корректность предположения, сделанного при оценке трудоемкости алгоритма формирования кривой «дракона»,  : :
 верно из условия первоначальной подстановки; верно из условия первоначальной подстановки;
- допустим истинность
 ; ;
- требуется доказать, что
 ; ;
- сначала подставим n+1 в рекуррентное соотношение:
 ; ;
- в правой части выражения можно произвести замену на основании индуктивной гипотезы:
  , что доказывает истинность первоначального предположения. , что доказывает истинность первоначального предположения.
Фрактальная размерность «салфетки» Серпинского согласно формуле (1) приобретает следующий вид:

9. «Ковер» Серпинского
Процесс формирования «ковра» Серпинского происходит следующим образом. Квадрат делится прямыми, параллельными его сторонам, на девять равных квадратов. Из квадрата удаляется внутренняя структура центрального квадрата. Получается множество, состоящее из восьми оставшихся квадратов первого ранга. Повторяя описанные выше действия с каждым из квадратов первого ранга, получим множество, состоящее из шестидесяти четырех квадратов второго ранга и т.д. На рис. 9 представлены первые четыре итерации формирования фрактальной структуры.
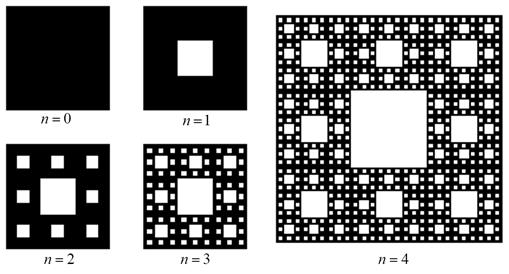
Рисунок 9. Формирование «ковра» Серпинского
Зависимость времени формирования фрактальной структуры «ковер» Серпинского представлена ниже:
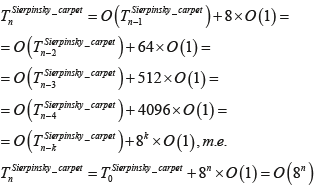 -87-93-web-resources/image/Formula_56.png)
Докажем корректность предположения, сделанного при оценке трудоемкости алгоритма формирования кривой «дракона»,  : :
 верно из условия первоначальной подстановки; верно из условия первоначальной подстановки;
- допустим истинность
 ; ;
- требуется доказать, что
 ; ;
- сначала подставим n+1 в рекуррентное соотношение:
 ; ;
- в правой части выражения можно произвести замену на основании индуктивной гипотезы:
  , что доказывает истинность первоначального предположения. , что доказывает истинность первоначального предположения.
Фрактальная размерность «ковра» Серпинского согласно формуле (1) приобретает следующий вид:

10. «Кладбище» Серпинского
Процесс формирования «кладбища» Серпинского происходит следующим образом: квадрат делится прямыми, параллельными его сторонам, на девять равных квадратов. Из исходного квадрата удаляется внутренняя структура каждого квадрата, являющаяся серединной для каждой строки и столбца соответственно. Получается множество, состоящее из четырех оставшихся квадратов первого ранга. Повторяя описанные действия выше с каждым из квадратов первого ранга, получим множество, состоящее из шестнадцати квадратов второго ранга и т.д. На рис. 10 представлены первые три итерации формирования фрактальной структуры.

Рисунок 10. Формирование «кладбища» Серпинского
Зависимость времени формирования фрактальной структуры «кладбище» Серпинского выражается следующим образом:
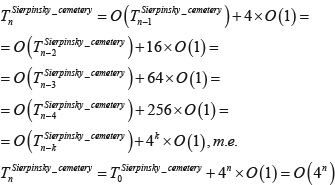 -87-93-web-resources/image/Formula_63.png)
Для доказательства истинности применим метод математической индукции:
докажем корректность предположения, сделанного при оценке трудоемкости алгоритма формирования кривой Коха,  : :
 верно из условия первоначальной подстановки; верно из условия первоначальной подстановки;
- допустим истинность
 ; ;
- требуется доказать, что
 ; ;
- сначала подставим n+1 в рекуррентное соотношение:
 ; ;
- в правой части выражения можно произвести замену на основании индуктивной гипотезы:
  , что доказывает истинность первоначального предположения. , что доказывает истинность первоначального предположения.
Фрактальная размерность «кладбища» Серпинского согласно формуле (1) приобретает следующий вид:

Выбор прототипа
Практические особенности задачи построения динамических трехмерных древовидных объектов определяют такие требования к фрактальным алгоритмам, как высокое быстродействие и низкая ресурсоемкость, а также практическую возможность отображения многообразия фрактальной структуры.
Как следует из приведенных выше результатов анализа, рассмотренные алгоритмы решают лишь задачу формирования двумерных фракталов и не удовлетворяют в полной мере предложенным требованиям.
Поэтому возникает практическая необходимость построения алгоритма решения поставленной проблемы, удовлетворяющего следующим функциональным критериям:
- приемлемая алгоритмическая сложность;
- древовидная структура;
- высокая фрактальная размерность;
- высокая детализация структуры.
Из приведенных выше результатов сравнительного анализа следует, что такие фрактальные алгоритмы, как кривая «дракона», Пифагорово дерево и двоичное дерево, имеют приемлемую алгоритмическую сложность в виде среди своих представителей и удовлетворяют критериям высокого быстродействия, низкой ресурсоемкости, не обладают органичностью структуры, имеют высокую фрактальную размерность в виде , причем такие алгоритмы, как Пифагорово дерево идвоичное дерево, имеют древовидную структуру.
В связи с вышеизложенным представляется практически необходимым построить метод, который представляет собой функциональное единство описанных выше алгоритмов, таких как кривая «дракона» и двоичное дерево, что позволяет сформировать трехмерную древовидную квазипериодичную структуру. Алгоритм двоичного дерева придаст структуре древовидный характер, а кривая «дракона» обеспечит приемлемую масштабную инвариантность каждой из компонент вычисленного древа.
Выводы
В результате проведенного сравнительного анализа практически востребованных алгоритмов формирования двумерных фракталов показано, что рассмотренные методы не удовлетворяют требованиям построения трехмерных объектов сзаранее определенной степенью детализации, что определяет практическую необходимость построения алгоритма, который бы решал поставленную проблему.
- Балханов В.К. Основы фрактальной геометрии и фрактального исчисления/ от. ред. Башкуев Ю.Б. – Улан-Удэ: Изд-во Бурятского госуниверситета, 2013. – 224 с.
- Божокин С.В., Паршин Д.А. Фракталы и мультифракталы. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 128 с.
- Мандельброт Б. Фрактальная геометрия природы. – М.: Институт компьютерных исследований, 2002. – 656 с.
- Морозов А.Д. Введение в теорию фракталов. – Москва-Ижевск: Институт компьютерных исследований, 2002. – 160 с.
- Томас Х. Кормен, Чарльз И. Лейзерон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ, 3-е изд./ Пер. с анг. – М.: ООО «И.Д. Вильямс», 2013. –1328 с.
- Федер Е. Фракталы/ Пер. с анг. – М.: Мир, 1991. – 254 с.
Ключевые слова: трехмерные фракталы, виртуальная реальность, построение динамических трехмерных объектов.
Analysis of calculating geometric fractal algorithms applied to the synthesis of three-dimensional, dynamic and tree-like structures
Teplov A.A., Master, MSTU Bauman, Department of “Software Information Technologies”, Moscow, teploff.aa@gmail.com
Maikov K.A., Doctor of Technical Sciences, Professor, MSTU Bauman, Department of “Software and Information Technologies”, Moscow, maikov@bmstu.ru
Abstract: The comparative analysis results of the virtually popular algorithms of two-dimensional fractals construction with high performance and low resource consumption are described in this article. The choice of the method for further modernization with the aim of building of dynamic, three-dimensional and tree-like objects with a certain degree of detail is justified.
Keywords: three-dimensional fractals, virtual reality, building of dynamic three-dimensional objects.
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
|
