|
|
|
|||||||||||||
|
|
Разработка математических моделей
|
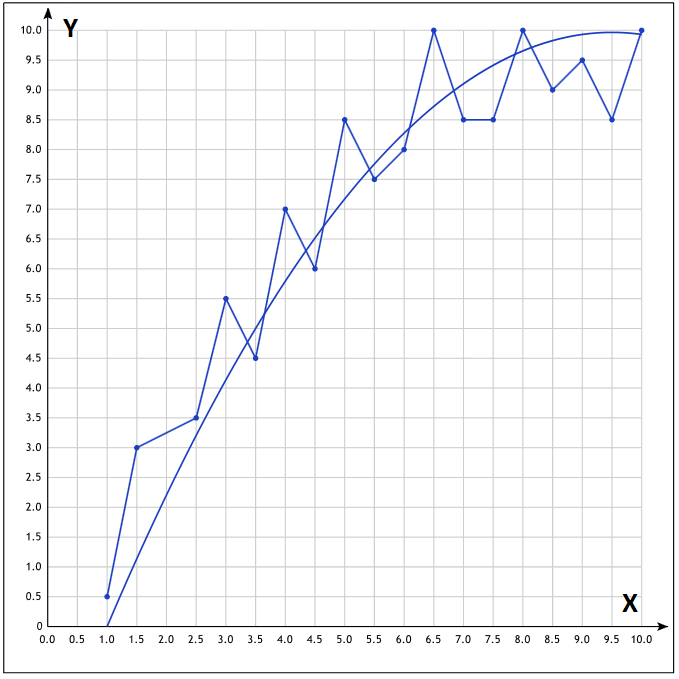
| X | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | -0,86 | -0,7 | -0,76 | -0,71 | -0,67 | -0,5 | -0,4 | -0,4 | -0,5 | -0,1 | 0 | 0,25 | 0,5 | 0,74 | 1 | 1,6 | 2,4 | 3,8 | 7 | 2 |
Для приближения функций широкое распространение получил метод наименьших квадратов (МНК) с полиноминальным видом:
f(x) = a0 + a1x + a2х2 +…
Однако полином не годится для приближения лавинных процессов, потому что плохо отражает участки стремительного роста сигналов, участки с крутыми фронтами.
Для моделирования таких процессов подходят дробно-рациональные функции вида:
Определим параметры, а и b методом наименьших квадратов (МНК).
Согласно методу МНК наилучшими параметрами a и b считают те, для которых сумма квадратов уклонений минимальна:
При моделировании функций деградационного изменения характеристических параметров некоторые данные получают, как правило, экспериментально в процессе эксплуатации в табличной форме.
При этом важно отметить, что фиксируют показатели конкретного устройства, работающего в конкретных условиях. По табличным данным именно контролируемого устройства нужно установить аналитические закономерности деградационного изменения его параметров и характеристик и по ним прогнозировать интервалы дальнейшей безопасной работы и ожидаемые моменты отказов, чтобы таким образом предотвратить опасность аварий. Наилучшие результаты в определении аналитических зависимостей обеспечивает метод наименьших квадратов (МНК).
Дробно-рациональные функции вида:
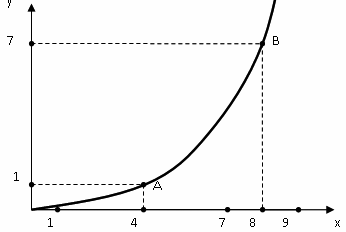
При х = 0 функция y = a0 = b/c. При х = b/a получаем y =0. При x → c функция y имеет вертикальную асимптоту x = c, таким образом отражает лавинно изменяющийся процесс, процесс с крутым фронтом. При b/a > c – лавинно растущий процесс, при b/a < c – лавинно падающий процесс. Качественные характеристики представлены на графике (см. рис. 3).
Рисунок 3. Деградационные изменения характеристического параметра при дробно-рациональном законе
Под лавинными понимают процессы стремительного изменения характеристических параметров (роста или спада). Деградационные лавинные процессы наступают в результате износа отдельных узлов или элементов. Для моделирования лавинных процессов с крутыми фронтами целесообразны дробно-линейные и степенные функции вида:
Для этой функции нормальную систему по МНК можно записать в виде:

-80-86-web-resources/image/Formula_05.png)
Анализ данной системы показывает, что она не линейна относительно коэффициентов и содержит слагаемые с a2, b2, ab, ac, bc.
Для упрощения нормальной системы по МНК предложено следующее:
- моделировать деградационные отклонения φ(xi) = y(xi) – a0;
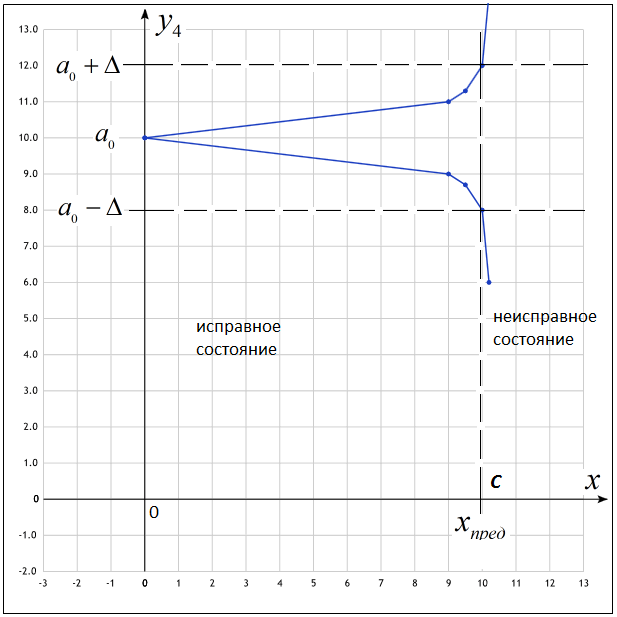
- при x = 0 функция y4 = a0, отсюда можно установить взаимную связь между параметрами b и c: b/c = a0, b/c = a0c;
- записать функцию y4 в виде:
Здесь a = (a0 + 1/p); с = q/p. Для нахождения p и q составим систему двух уравнений по МНК:
Если в эту систему ввести обозначения
то нормальную систему уравнений по МНК для рассматриваемой системы можно записать в виде:
Решение этой системы позволит определить параметры функции φ4(x) и далее y(x).
- Достоинства моделирования деградационных изменений характеристических параметров лавинного типа:
- Параметры аналитической зависимости процесса насыщения могут быть установлены на начальных этапах его наблюдения.
- По начальному наблюдению можно прогнозировать показатели и характеристики для последующих моментов.
- Для определения параметров искомой аппроксимирующей функции необходимы координаты n ≥ 3 точек. По МНК чем больше точек экспериментальной функции получено, тем лучше. И все данные используются для расчета параметров.
- На каждом этапе наблюдения параметры аналитической зависимости можно уточнять и, таким образом, вернее прогнозировать последующий ход процесса. Последнее особенно важно при определении моментов отказа технических устройств и при определении сроков их безотказной работы.
- Эффективность решения задач в значительной мере зависит от точности идентификации деградационных процессов рассматриваемых объектов при их эксплуатации. Но использование модемного анализа позволяет несколько снизить требования к точности за счет применения методов наименьших квадратов (МНК) и др. Они позволяют получить положительные результаты, связанные с эксплуатационной надежностью, с оценкой состояния объектов иустановлением возможного предела их эксплуатации.
- Для прогноза состояния многорежимных объектов рассмотрен пример с использованием нелинейной регрессионной модели объекта, полученной в результате предварительного многофакторного эксперимента. Работоспособность предложенной методики подтверждена путем реализации центрально-композиционного плана испытаний центробежного насоса при исследовании влияния на его виброактивность степени изношенности подшипника и режимных факторов (частоты вращения и давления смазки).
Для реализации программы мною был выбран язык C# и СУБД Microsoft Office Access.
Программа состоит из двух форм:
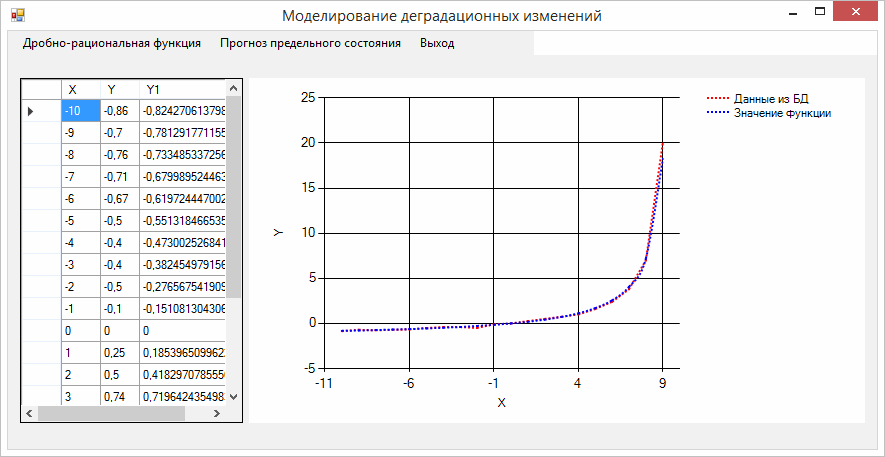
1) Форма «Моделирование деградационных изменений» – основная форма программы, содержащая управляющее меню, с помощью которого можно выполнить следующие действия (см. рис. 4):
- «Дробно-рациональная функция» → «Данные из БД» – открытие файла базы данных, содержащего данные характеристических параметров (X,Y).
- «Дробно-рациональная функция» → Форма «Ввод данных вручную» – вызвать форму для ввода данных вручную.
Рисунок 4. Форма «Моделирование деградационных изменений»
Эти действия позволят провести исследование лавинных процессов.
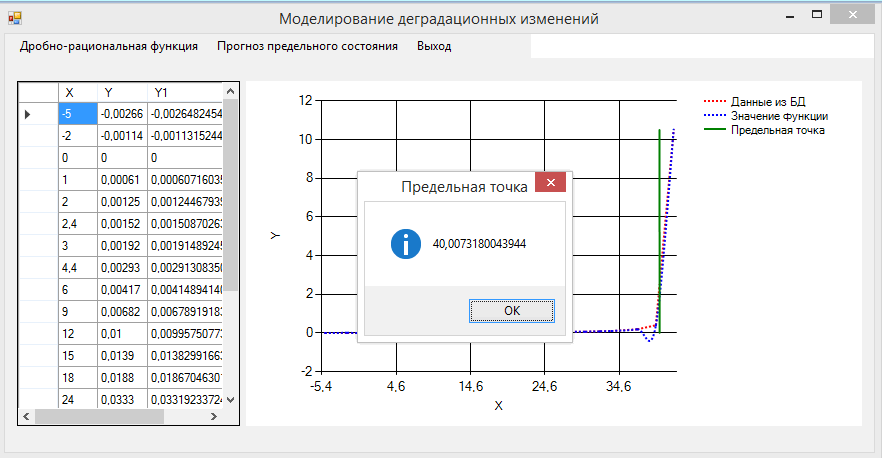
- «Прогноз предельного состояния» → «Данные из БД» – открытие файла базы данных, содержащего данные характеристических параметров (X,Y).
- «Прогноз предельного состояния» → Форма «Ввод данных вручную» – вызвать форму для ввода данных вручную.
Эти действия позволят провести анализ деградационных изменений и вычислить прогноз предельного состояния.
- «Выход» – завершение работы программы.
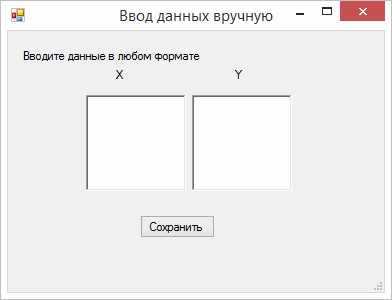
2) Форма «Ввод данных вручную» позволяет ввести данные характеристических параметров вручную в любом удобном формате (через пробел, перевод строки, числа двойной точности понятны программе как с запятой, так и с точкой) (см. рис. 5).
Рисунок 5. Форма «Ввод данных вручную»
Рассмотрим примеры из написанного кода программы.
Класс Stack{} – класс, необходимый для хранения данных характеристических параметров, которые доступны и известны в любой части программы.
public class Stack
{
public static ArrayList x = new ArrayList();
public static ArrayList y = new ArrayList();
public static ArrayList y1 = new ArrayList();
public static void PushX(object o)
{ x.Add(o);}
public static void PushY(object o)
{ y.Add(o); }
public static void PushY1(object o)
{ y1.Add(o); }
}
1) Исследование лавинных процессов.
private void данныеИзБДToolStripMenuItem_Click(object sender, EventArgs e)
{
if (Class2.Connect() == 0)
{
object[] A = { "Файл не выбран" };
MessageBox.Show(String.Format(" {0}", A));
}
else
{
chart1.Series.Clear();
richTextBox1.Visible = false;
Class1 class1 = new Class1();
class1.select();
M_N_K();
dataGridView();
Chart();
}
}
Статический класс Class2{} позволяет пользователю во время работы программы выбрать любую базу данных. База данных должна содержать таблицу «data» со столбцами «X» и «Y».
Класс Class1{} представляет собой класс шаблона проектирования «шлюз», взаимодействующего с базой данных, которую выберет пользователь.
Функция M_N_K() реализует метод наименьших квадратов и метод Крамера:
private void M_N_K()
{
double a = 0; double b = 0; double x = 0;
double y = 0; double sx = 0; double sy = 0;
double S2 = 0; double S3 = 0; double T1 = 0;
double T2 = 0; double T3 = 0; double D = 0;
double Da = 0; double Db = 0;
for (int i = 0; i < Stack.x.Count; i++)
{
x = Convert.ToDouble(Stack.x[i]);
y = Convert.ToDouble(Stack.y[i]);
sx += x;
sy += y;
S2 += x * x;
S3 += x * x * x;
T1 += x * y;
T2 += (x * x) * y;
T3 += (x * x * x) * y;
}
D = T2 * T2 - T1 * T3;
Da = S2 * T2 - T1 * S3;
Db = T2 * S3 - S2 * T3;
a = Da / D;
b = Db / D;
for (int i = 0; i < Stack.x.Count; i++)
{
Stack.PushY1((Convert.ToDouble(Stack.x[i])) / (a * (Convert.ToDouble(Stack.x[i])) + b));
}
}
Функция dataGridView() выводит значения характеристических параметров в виде таблицы.
Функция Chart() выводит графическое изображение деградационных изменений.
2) Анализ деградационных изменений и прогноз предельного состояния.
private void данныеИзБДToolStripMenuItem1_Click(object sender, EventArgs e)
{
if (Class2.Connect() == 0)
{
object[] A = { "Файл не выбран" };
MessageBox.Show(String.Format(" {0}", A));
}
else
{
chart1.Series.Clear();
richTextBox1.Visible = false;
Class1 class1 = new Class1();
class1.select();
double x_Pr = Pr_S();
Chart();
dataGridView();
Chart_Pr(x_Pr);
}
}
Функция Pr_S() реализует метод наименьших квадратов и поиск предельного состояния:
private double Pr_S()
{
double p = 0; double q = 0; double x = 0;
double y = 0; double S2 = 0; double S3 = 0;
double T1 = 0; double T2 = 0; double T3 = 0;
double D = 0; double Dp = 0; double Dq = 0;
double Pr = 0.5; double x_Pr = 0;
for (int i = 0; i < Stack.x.Count; i++)
{
x = Convert.ToDouble(Stack.x[i]);
y = Convert.ToDouble(Stack.y[i]);
S2 += x * x;
S3 += x * x * x;
T1 += x * y;
T2 += (x * x) * y;
T3 += (x * x * x) * y;
}
D = T2 * (-T2) - (-T1) * T3;
Dp = S2 * (-T2) - (-T1) * S3;
Dq = T2 * (S3) - S2 * T3;
p = Dp / D;
Console.WriteLine(p);
q = Dq / D;
Console.WriteLine(q);
for (int i = 0; i < Stack.x.Count; i++)
{
Stack.PushY1((Convert.ToDouble(Stack.x[i])) / (p * (Convert.ToDouble(Stack.x[i])) - q));
}
x_Pr = Pr * q / (Pr * p - 1);
Console.WriteLine(x_Pr);
return x_Pr; }
Результат работы программы (см. рис. 6-8).
Рисунок 6. Выбор файла базы данных
Рисунок 7. Исследование лавинных процессов
Рисунок 8. Анализ деградационных изменений и прогноз предельного состояния
Основные результаты работы:
- Разработаны регрессионные математические модели деградационных изменений лавинного типа для однопараметрических и многопараметрических зависимостей.
- Новизна задачи:
- Моделирование деградационных отклонений характеристик электротехнических устройств на основе обработки временных рядов методом наименьших квадратов, что снизило размерность задачи.
- Приведена методика оценки и прогнозирования остаточного ресурса электротехнических устройств.
- Практическая значимость:
- Разработан программный комплекс анализа деградационных изменений характеристик элементов электротехнических устройств.
- Выполнен прогноз экстраполяции в заданных условиях, проведен вычислительный эксперимент. eof
- Лоскутов А. Ю. Анализ временных рядов. Курс лекций. – М.: Физический факультет МГУ, (год неизвестен). – 113 с.
- Лоскутов А. Ю., Михайлов А. С. Основы теории сложных систем. – М.: Регулярная и хаотическая динамика, 2007. – 620 с.
- G ouesbet G., Meunier – Guttin – Cluzel S., Menard O. (eds) Chaos and Its Reconstruction (New York: Nova Sci. Publ., 2003).
- Безручко Б. П., Смирнов Д. А. Математическое моделирование и хаотические временные ряды. – Саратов: ГосУНЦ «Колледж», 2005. – 320 с.
- Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1966. – 664 с.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. – М.:Бином, 2003. – 630 с.
Ключевые слова: деградационные процессы, метод наименьших квадратов, нелинейные уравнения, лавинный процесс, многофакторная модель, линейная регрессионная модель, С#, Microsoft Office Access, дробно-рациональная функция, метод Крамера, экстраполяция, теорема Гаусса-Маркова.
Development of mathematical models of avalanche-type degradation processes using the method of least squares
Egorova MV., Moscow Aviation Institute (National Research University), 812 Chair, Lead Engineer
Abstract: This article presents a model of degradation processes based on a simple interface and having great functionality. The system allows you to get rid of problems in predicting the failure of operated electrical devices. To implement this program was chosen programming language C # and DBMS Microsoft Office Access. In this program consists of 2 forms: the form "Modeling of degradation changes" and the form "Entering data manually". All information is stored in files of the accdb format (you can open this file using the Microsoft Office Access program), for the possibility of making changes to users who do not have experience with the DBMS.
Keywords: degradation processes, least-squares method, nonlinear equations, avalanche process, multifactor model, linear regression model, C #, Microsoft Office Access, fractional-rational function, Cramer method, extrapolation, Gauss-Markov theorem.
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 Егорова М.В., Московский авиационный институт (национальный исследовательский университет), 812 кафедра, ведущий инженер
Егорова М.В., Московский авиационный институт (национальный исследовательский университет), 812 кафедра, ведущий инженер