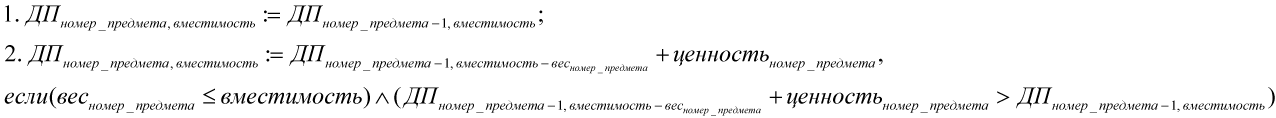 |
|
|
|
Как уложить ранец и рюкзак?
Как уложить ранец и рюкзак? В публикации рассматривается классическая задача динамического программирования об укладке ранца (рюкзака), вариант 0-1 Достаточно часто при решении вычислительных задач прикладной математики возникают ситуации, связанные с загрузкой определенных предметов в один. А именно происходит выбор некоторого подмножества из конечного счетного множества элементов. Элементы характеризуются условными признаками веса и ценности. Необходимо, чтобы элементы выбранного подмножества обладали наибольшей суммарной ценностью, при этом не превосходя некоторой предельной вместимости ранца. Наиболее хорошо изученной является задача о ранце 0-1. В этой задаче [1, 2] предполагается, что для каждого предмета происходит выбор не более одного экземпляра. Пусть имеется N предметов, а максимальная вместимость ранца есть M. N и M – целые положительные числа. Для каждого предмета, i от 1 до N, известны вес и ценность. Удобно организовать два вектора целых положительных чисел для их хранения, а именно вес [1:N] и ценность [1:N], при этом вес [i] и ценность [i] соответственно вес и ценность i-го предмета. Удобно ввести целые положительные переменные:
При решении задачи с использованием динамического программирования необходимо использовать таблицы. В данном случае будет использоваться двухмерный массив целых неотрицательных чисел ДП [0:N, 0:M] – массив ценностей. Строка таблицы (первый индекс массива) – это номер рассматриваемого элемента, столбец таблицы (второй индекс массива) – предельное значение вместимости. В начальном случае, когда первый или второй индексы равны нулю, значение ДП [] равно нулю. Это очевидно, поскольку если никакие элементы не рассматриваются либо невозможно ничего положить в ранец, то ценность нулевая. Начальное значение других элементов ДП [] неопределенно, но может быть для удобства задано равным нулю. Так же как и при решении любых задач динамического программирования, необходимо построить рекуррентные соотношения, на основании которых будет производиться переход от частных подзадач к более общим. Будем рассматривать подзадачи в порядке по строкам – номер предмета от 1 до N, по столбцам – вместимость от 1 до M, как типовую задачу по обходу двухмерного массива. При этом при рассмотрении элемента ДП [номер_предмета, вместимость] необходимо присвоить ему некоторое значение. Возникает две ситуации выбора из подзадач, а именно:
Ситуация (1) возникает тогда, когда вес рассматриваемого предмета строго больше, чем текущее значение вместимости, то есть если вес [номер_предмета] > вместимость. При этом очевидно, что значение в рассматриваемой ячейке ДП [] будет равно значению в ячейке ДП [] того же столбца, но на одну строку выше, то есть ДП [номер_предмета, вместимость] := ДП [номер_предмета–1, вместимость] Ситуация (2) возникает тогда, когда вес рассматриваемого предмета не превышает текущего значения вместимости, то есть если вес [номер_предмета] ≤ вместимость. В этой ситуации можно либо (2.1) использовать предмет, либо (2.2) не использовать его, в зависимости от того, в каком случае значение ДП [] больше, а именно необходимо найти максимальное значение из ДП [(2.1)] и ДП [(2.2)]. Расчет для ДП [(2.1)] соответствует (1), как ДП [номер_предмета, вместимость] := ДП [номер_предмета–1, вместимость] Расчет для ДП [(2.2)] несколько сложнее. Это вызвано тем, что при этом (2.2.а) вместимость подзадачи должна быть меньше рассматриваемой вместимости на величину веса предмета и (2.2.б) рассматриваемая ДП [] должна быть больше ДП [] подзадачи на величину ценности предмета. При объединении (2.2.а) и (2.2.б) получается ДП [номер_предмета, вместимость] := ДП [номер_предмета–1, вместимость – вес [номер_предмета]] + ценность [номер_предмета] Окончательно приходим к рекуррентному соотношению (1) для заполнения таблицы в порядке по строкам – номер предмета от 1 до N, по столбцам – вместимость от 1 до M (см. формулу 1).
Формула 1 Соотношение (1) может быть удобно переписано для языков программирования, в которых отсутствует стандартная библиотечная функция нахождения максимума двух чисел, в форме из двух последовательных шагов (2) (см. формулу 2).
Формула 2 При этом наибольшей ценностью предметов, которые можно поместить в емкость, является величина в ДП [N, M]. Теперь необходимо получить номера предметов, которые в этом решении должны быть помещены в ранец. На этом этапе номер рассматриваемого предмета изменяется от N до 1, а вместимость уменьшается начиная с M.
Указанные соотношения реализуются как алгоритм на школьном алгоритмическом языке. В листинге 1 приводится решение задачи для N = 5, M = 10, вес = [1, 2, 3, 4, 5], ценность = [4, 5, 6, 7, 8]. Затем этот алгоритм реализовывается как программа на языках программирования высокого уровня Java, Pascal, Python (с переводом идентификаторов переменных на английский язык). Соответствующие листинги, равно как и листинг 1 для системы КуМир, доступны на сайте http://samag.ru. Листинг 1. Реализация на школьном алгоритическом языке алг Ранец
нач
цел таб вес[1:5], ценность[1:5]
цел таб ДП[0:5, 0:10]
цел номер_предмета, вместимость
вес[1] := 1; вес[2] := 2
вес[3] := 3; вес[4] := 4
вес[5] := 5
ценность[1] := 4; ценность[2] := 5
ценность[3] := 6; ценность[4] := 7
ценность[5] := 8
ДП[0, 0] := 0
нц для номер_предмета от 1 до 5
ДП[номер_предмета, 0] := 0
кц
нц для вместимость от 1 до 10
ДП[0, вместимость] := 0
кц
нц для номер_предмета от 1 до 5
нц для вместимость от 1 до 10
ДП[номер_предмета, вместимость] := ДП[номер_предмета - 1, вместимость]
если вес[номер_предмета] <= вместимость
то
если ДП[номер_предмета - 1, вместимость - вес[номер_предмета]] + ценность[номер_предмета] > ДП[номер_предмета - 1, вместимость]
то
ДП[номер_предмета, вместимость] := ДП[номер_предмета - 1, вместимость - вес[номер_предмета]] + ценность[номер_предмета]
все
все
кц
кц
вывод "Максимум: ", ДП[5, 10]
вывод ". Предметы:"
вместимость := 10
нц для номер_предмета от 5 до 1 шаг -1
если ДП[номер_предмета, вместимость] <> ДП[номер_предмета - 1, вместимость]
то
вывод " ", номер_предмета
вместимость := вместимость - вес[номер_предмета]
все
кц
кон
Протокол отладки программы из листинга 1 приводится в листинге 2, а результат выполнения за 525 шагов – в последующем выводе. Листинг 2. Протокол отладки вес[1]=1; вес[2]=2
вес[3]=3; вес[4]=4
вес[5]=5
ценность[1]=4; ценность[2]=5
ценность[3]=6; ценность[4]=7
ценность[5]=8
ДП[0,0]=0
номер_предмета=5
ДП[5,0]=0
вместимость=10
ДП[0,10]=0
номер_предмета=5
вместимость=10
ДП[5,10]=22
да
нет
ДП[4,10]=22
вместимость=10
номер_предмета=1
да
вместимость=0
Результат выполнения: Максимум: 22. Предметы: 4 3 2 1 Таким образом, в публикации рассматривается решение классической задачи динамического программирования, выполняется построение рекуррентных соотношений и алгоритма. Реализацию на Java, Pascal, Python и КуМир можно скачать с сайта журнала. eof
|
КИРИЛЛ ТКАЧЕНКО, инженер 1-й кат., ФГАОУ ВО «Севастопольский государственный университет», 
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
