|
|
|
|||||||||||||
|
|
Взаимные функциональные зависимости Обычно к системному администратору обращаются по самым разным вопросам, при возникновении любой проблемы: будь это забытый пароль, неработающая программа, не читающаяся дискета или пропавшие неизвестно куда данные. Этот список можно продолжать бесконечно. Мне хотелось бы остановиться на ошибках, которые возникают при работе с СУБД. Статья посвящена тем, кому приходится заниматься вопросами проектирования или реструктурирования реляционных баз данных. В настоящее время базы данных являются частью практически любой информационной системы. Современные БД характеризуются большой размерностью и сложной структурой, поэтому для их разработки используются специальные программные средства. Они позволяют не только упростить и ускорить процесс проектирования, но и выполнять некоторые функции по оптимизации БД. Наиболее популярным является подход, в котором осуществляется нормализация. Теория нормализации (зависимостей) появилась одновременно с теорией реляционной алгебры. Коддом были предложены первые нормальные формы. Впоследствии, третья нормальная форма была уточнена и названа нормальной формой Бойса-Кодда (НФБК). Позже Фэйджином (Fagin) были предложены 4 и 5 нормальная формы, а также альтернативная доменно-ключевая нормальная форма [3]. Существуют и другие нормальные формы, но наиболее популярной является 3НФ и НФБК. В основе теории нормализации лежат различные понятия зависимостей между атрибутами БД. В теории Кодда используется понятие функциональной зависимости (ФЗ), реляционный аналог математической функции. Рассмотрение основных вопросов статьи требует четкого определения понятия ФЗ, поэтому приведем формальное определение ФЗ из 6-ого издания книги Дейта [4]. Отметим сразу, что статья ориентирована на читателя, знакомого с основными понятиями реляционной алгебры и теории нормализации. Пусть R – это отношение, а X и Y – произвольные подмножества множества атрибутов отношения R. Тогда Y функционально зависимо от X (X–>Y), тогда и только тогда, когда каждое значение множества X отношения R связано в точности с одним значением множества Y отношения R. Иначе говоря, если два кортежа отношения совпадают по X [t1(X) = t2(X)], то они также совпадают и по Y [t1(Y) = t2(Y)]. X–>Y <=> [t1(X) = t2(X)] => [t1(Y) = t2(Y)] Возможность применения правил Армстронга Проектирование схемы базы данных начинается с определения универсального отношения, в которое входят все атрибуты. Для предметной области задается множество ограничений с помощью функциональных, многозначных и других зависимостей. Для вывода новых ФЗ или сокращения их числа используются правила Армстронга. Эти правила общеизвестны и приводятся почти в каждой книге по БД. Однако ни в одной из них не говорится об ограниченности их использования. Рассмотрим пример использования правила объединения: Если A–>B, A–>С то A–>BС Пусть имеется два простейших отношения ЗАРПЛАТА(Сотрудник, Зарплата) и СЧЕТА(Сотрудник, N_Кредитки). Во второй таблице задаются номера кредитных карточек сотрудников. Предположим, что у Невезинского нет кредитки. Специалист по БД решил оптимизировать структуру и устранить избыточность, пользуясь вышеупомянутым правилом. Если Сотрудник –> Зарплата, Сотрудник –> N_Кредитки то Сотрудник –> {Зарплата, N_Кредитки}
Сразу после «оптимизации» в результирующем отношении появится кортеж, который имеет пустое (неопределенное) значение. Реляционное отношение, да и ФЗ (A–>BС) таких кортежей не поддерживают, поэтому такая запись должна автоматически удалиться. Большинство современных СУБД поддерживают трехзначную логику (с использованием Null значений), поэтому запись может не пропасть. Однако наличие неопределенных значений приводит к появлению неоднозначности в запросах и программах. Таким образом, свободно применять правила Армстронга можно только для проектируемой БД, не имеющей данных. При реструктуризации необходимо использовать Null-значения. Это замечание существенно для баз данных с динамически изменяемой структурой, к которым можно отнести современные объектно-реляционные разработки. Функциональные зависимости являются одними из простейших семантических ограничений, поэтому можно смело утверждать, что все рассматриваемые вопросы будут актуальны и для объектных СУБД. Проблемы 3НФ и НФБК Приведение отношений в 3НФ и НФБК направлено на избавление от транзитивных зависимостей (A–>B, B–>C => A–>C). 3НФ позволяет удалить транзитивные зависимости не ключевого атрибута (C) от ключевого (A) через другой не ключевой (B). В НФБК запрещаются все зависимости среди ключевых атрибутов и любой не ключевой атрибут должен напрямую (не транзитивно) зависеть от ключа, т.е. от всех ключевых атрибутов. Рассмотрим пример приведения отношения в третью нормальную форму, предложенный Ульманом [18] и проблемы, которые при этом возникают. Пусть задана схема отношений R и множество функциональных зависимостей F. Звездочкой (*) помечены функциональные зависимости, которые отсутствуют в указанном примере. R = (A, B, C, D, E, T), где:
F = {CD–>B, CD–>A, AC–>D, CE–>A, A–>B, CB–>D, AE–>T, CE–>D}
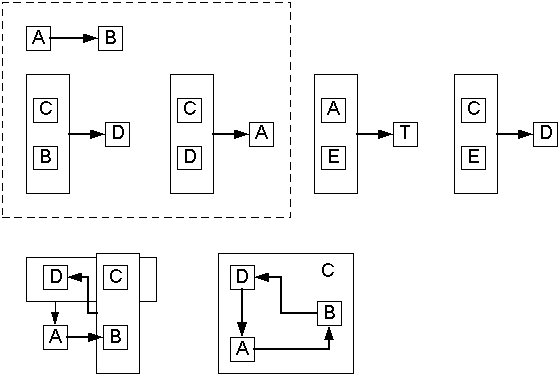
Для приведения схемы отношения в 3НФ необходимо найти минимальное покрытие множества функциональных зависимостей. В описываемом примере оно будет представлено следующим образом [18]: F = {A–>B, CD–>A, CB–>D, AE–>T, CE–>D} Далее, осуществим декомпозицию схемы отношения: r={AB, CDA, CBD, AET, CED} Данная схема находится в НФБК и декомпозируется из исходной схемы с сохранением зависимостей. Недостатком этой декомпозиции является зависимость проекций (по терминологии Риссанена). Отсюда следует, что схема может обладать аномалиями. Проиллюстрируем это на примере: На рис. 1. представлены три таблицы из полученной схемы отношений. Звездочками отмечены ключевые поля. Пусть в БД хранится информация, что в 10 часов в 12 и 13 аудиториях должны читаться курсы «Базы данных» и «Операционные системы» (CDA). Известно, что эти курсы читают соответственно преподаватели Иванов и Петров (AB). При этом оба преподавателя должны проводить занятия одновременно в одной аудитории (CBD). Данная информация является противоречивой, несмотря на то, что схема отношений находится в НФБК и все условия ФЗ соблюдены.
Рисунок 1. Противоречивость БД Представим теперь, что D – это номер посадочной полосы самолетов с номером рейса из B. По условиям, заданным набором ФЗ такая ситуация невозможна. И тем не менее, в БД, находящейся в НФБК с «сохранением» зависимостей содержится неутешительный приговор двум самолетам. Рассмотрим другой случай. Пусть D – это сумма в размере 120000$ и ее нужно перечислить только на счет Иванова. Как видно из рис. 1. эту сумму может также получить и Петров, а также десятки других сотрудников и это не будет противоречить структуре БД. Из примера видно, что приведение отношения в 3НФ или даже в НФБК с помощью декомпозиции не решает проблемы противоречивости хранимых данных. Конечно, если произвести естественное соединение всех отношений, то мы избавимся от всех противоречий. Обеспечение целостности по взаимосвязанности требует использования специальных средств: внешних ключей, представлений, ограничений на целостность, триггеров и т. д. Взаимные функциональные зависимости Оставшаяся часть статьи посвящена вопросу обнаружения и устранения ошибок, описанных выше. Рассматриваемая противоречивость данных связана с тем, что во множестве ФЗ имеются взаимные функциональные зависимости (ВФЗ). Взаимной функциональной зависимостью атрибутов A и B называется пара функциональных зависимостей вида B–>A, A–>B и обозначается как A<–>B. Рассмотрим основное свойство ВФЗ. Из функциональной зависимости A–>B вытекает утверждение 1. Кроме того, может существовать множество кортежей с разными значениями в атрибуте А и одинаковыми значениями в атрибуте B (утверждение 2): (1) A–>B <=> [ti(A) = tj(A)] => [ti(B) = tj(B)] (2) [Для любых ti(B)] существует {t(A)} , |{t(A)}| ≥ 1 Аналогично определим соотношения для ФЗ B–>A: (3) B–>A <=> [ti (B) = tj (B)] => [ti (A) = tj (A)] (4) [Для любых ti (A)] $ {t(B)} , |{t(B)}| ≥ 1 Соединяя условия (1), (4) и (2), (3) получаем следующие утверждения: (5) [Для любых ti (A)] $ {t(B)} , |{t(B)}| = 1 (6) [Для любых ti (B)] $ {t(A)} , |{t(A)}| = 1 Основным свойством ВФЗ является взаимная однозначность значений для атрибутов левой и правой части, т.е. каждый кортеж должен иметь уникальные значения полей, входящих во ВФЗ. Для задания ВФЗ в СУБД необходимо атрибуты A и B объединить в одном отношении (таблице) и задать уникальность каждого атрибута. Если части ВФЗ более одного атрибута, то можно использовать первичный и альтернативный ключ (с обязательным заданием уникальности). Надо отметить, что алгоритмы нахождения минимального покрытия Мейера [11] и Бернштейна [19] учитывают ВФЗ, но только в рамках сокращения размера покрытия. Для дальнейшего рассмотрения материала введем понятие условной ВФЗ (УВФЗ). Условной взаимной функциональной зависимостью атрибутов A и B называется пара функциональных зависимостей вида СB–>A, СA–>B, где С – набор атрибутов (условие) такой, что С –> AB. Будем обозначать УВФЗ как С|A<–>B. Смысл УВФЗ заключается в том, что при определенных условиях атрибуты находятся во взаимной функциональной зависимости. Из функциональной зависимости CA–>B вытекают утверждения 7 и 8: (7) CA–>B <=> [ti(C) = tj(C)]&[ti(A) = tj(A)] => [ti(B) = tj(B)] (8) [Для любых ti(B)] $ {t(СA)} , |{t(СA)}| ≥ 1 Аналогично определим соотношения для ФЗ СB–>A: (9) СB–>A <=> [ti(C) = tj(C)]&[ti(B) = tj(B)] => [ti(A) = tj(A)] (10) [Для любых ti(A)] $ {t(СB)} , |{t(СB)}| ≥ 1 Соединяя условия (7-10) и фиксируя значение атрибута С, получаем следующие утверждения: (11) [Для любых ti(A)] $ {t(B)} , |{t(B)}| = 1 (12) [Для любых ti(B)] $ {t(A)} , |{t(A)}| = 1 Основным свойством EВФЗ является взаимная однозначность значений для атрибутов левой и правой части при совпадении значений в атрибутах условия, т.е. каждый для каждого значения атрибутов условия кортеж должен иметь уникальные значения полей, входящих во ВФЗ. Существует несколько способов задать УВФЗ. Можно ввести понятие условного ключа или условной уникальности. Проиллюстрируем эти понятия. Пусть имеется условная взаимная зависимость (УВФЗ) такая, что условием является набор атрибутов C, атрибуты B и D входят во ВФЗ. Тогда при фиксированном значении атрибутов из С значения атрибутов B и D являются уникальными. Для пояснения приведем пример. В настоящее время возможность введения таких ключей в СУБД отсутствует, поэтому данное ограничение можно реализовать либо программным способом, либо декомпозицией отношений и дополнительных изменений схемы. К первому способу можно отнести возможность работы с представлениями (запросами на отображение). Если реализовать ввод данных только через представление, тогда оно должно содержать выборку по одному из значений условных атрибутов (например С1), а взаимозависимые атрибуты должны иметь уникальный ключ. CREATE VIEW UslFD AS SELECT Pse1.* FROM table1 AS Pse1, table1 AS Pse2 WHERE (Pse1.C= Pse2.C) & (Pse1.A<-> Pse2.A) & (Pse1.B<-> Pse2.B)
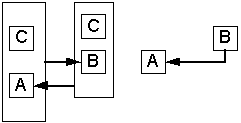
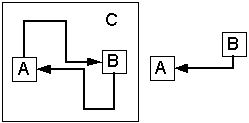
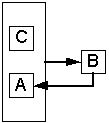
При наборе условных атрибутов (C1,.. Cn) конструкция Where изменится: WHERE (Pse1.C1= Pse2.C1) &(Pse1.C2= Pse2.C2) &…& (Pse1.Cn= Pse2.Cn)& (Pse1.A<-> Pse2.A) & (Pse1.B<-> Pse2.B) Альтернативой может послужить общее ограничения на целостность БД. CREATE ASSERTION UslFD CHECK ( SELECT Pse1.* FROM table1 AS Pse1, table1 AS Pse2 WHERE (Pse1.C= Pse2.C) & (Pse1.A<-> Pse2.A) & (Pse1.B<-> Pse2.B) ) Вторым способом задания ограничений является соответствующая организация структуры БД (схемы). Реализовать ограничение в одном отношении можно путем задания двух ключей (первичного и альтернативного) со свойством уникальности. Можно также осуществить декомпозицию с использованием внешних ключей. Выявление ВФЗ Рассмотрим теперь причины возникновения взаимных функциональных зависимостей и методы их выявления, а также некоторые важные следствия и их применимость на этапе проектирования структуры базы данных. Следствие 1 Во всех функциональных зависимостях, в которых присутствует набор условных атрибутов (С) и условная взаимная ФЗ (CA–>B, CB–>A), можно воспользоваться правилом A~B для нахождения минимального (канонического) покрытия. Пример: F = {CD–>B, AC–>D, CE–>A, A–>B, CD–>A, CB–>D, AE–>T, CE–>D} CD–>B & CB–>D => B–>D & D–>B => C| D<=>B Выберем все зависимости, в которых присутствует C: CD–>B, AC–>D, CE–>A, CD–>A, CB–>D, CE–>D Заменим B на D и получим: CD–>D, AC–>D, CE–>A, CD–>A, CD–>D, CE–>D Сократим одинаковые зависимости (CD–>D). Полученная зависимость CD–>D является рекурсивной. В исходных данных такой зависимости нет, поэтому можно проверить предметную область на ее наличие. В случае ее обнаружения необходимо разбить ее на не рекурсивные зависимости. В общем (данном) случае рекурсии нет, поэтому эту функциональную зависимость исключаем из списка как тривиальную. AC–>D, CE–>A, CD–>A, CE–>D, C| D<=>B Аналогично поступаем и AC–>D и CD–>A CE–>A, C| A<=>D<=>B Итоговое множество функциональных зависимостей будет выглядеть следующим образом: F = { A–>B, AE–>T, CE–>A, C| A<=>D<=>B} Следствие 2 Более простые УВФЗ включают в себя более сложные. Если имеется две УВФЗ такие, что множество условных атрибутов одной зависимости входит во множество условных атрибутов другой зависимости, то такая УВФЗ является более простой: C|A<–>B и D|A<–>B, и CID, то C|A<–>B => D|A<=>B Следствие 3 Нахождение минимального покрытия ФЗ не убирает и не изменяет ВФЗ, но значительно осложняет их поиск. В качестве примера можно сравнить очевидность ВФЗ в исходном и нормализированном наборе ФЗ (см. выше). Одним из способов обнаружения ВФЗ является графическое отображение ФЗ и поиск кольцевых структур. CA–>B, B–>A На рис. 2а показаны функциональные зависимости в графической форме. Можно заметить, что функциональные зависимости пересекаются, и, кроме того, образуют циклическую структуру. Воспользовавшись правилом дополнения Армстронга, получаем схему, представленную на рис. 2б. Функциональная зависимость B–>A представлена отдельно и атрибут B в ней не зависит от CA, т.к. зависимость была разделена на B–>A при наличии C и на B–>A при отсутствии C. На рис. 2в представлено выделение взаимной зависимости A и B при условии С. Рисунок 2а. Графическое выявление ВФЗ Рисунок 2б. Графическое выявление ВФЗ Рисунок 2в. Графическое выявление ВФЗ На рис. 3 рассматривается пример нахождения УВФЗ для минимального покрытия ФЗ из примера, приведенного выше. В результате нахождения минимального покрытия ВФЗ становятся менее очевидными из-за увеличения элементов в цикле. Взаимные зависимости становятся транзитивными. Рисунок 3. Поиск УВФЗ для минимального покрытия Можно сделать вывод, что нахождение минимального покрытия ФЗ усложняет процесс нахождения ВФЗ за счет уменьшения числа зависимостей. Тем не менее, нахождение минимального покрытия необходимо для получения 3НФ, а некоторые ВФЗ могут быть исходно неочевидны и для их выявления требуется ввести специальный алгоритм. Единственное, что можно посоветовать, это проверка на ВФЗ каждой ФЗ, которую можно исключить из начального списка ФЗ. Ниже приводится алгоритм нахождения ВФЗ для минимального покрытия. Данный алгоритм является схематичным и неоптимизированным, т.к. при нахождении ВФЗ не осуществляется изменение (уменьшение) множества исходных ФЗ. Можно также заранее исключить зависимости, которые точно не образуют ВФЗ. Это так называемые неприводимые слева ФЗ, т.е. те зависимости, в левой части которых содержатся атрибуты, не встречающиеся в правой части других ФЗ. Алгоритм можно также применять для произвольного множества ФЗ, но в случае минимального покрытия ВФЗ будут находится только один раз. Существуют множества ФЗ, которые являются взаимно-независимые. Правила определения таких множеств можно найти в [4,20]. Пусть задана схема отношений R и множество ФЗ S такие что: S ={ X[1]–>Y[1]… X[i]–>Y[i]… X[n]–>Y[n]}, где n – количество ФЗ. Y[i] принадлежит R, X[i] подмножество R т.е. Y является атрибутом, а X – набором атрибутов из R. X[i]= {X[i][1]… X[i][j]… X[i][m]} где m – Количество атрибутов в левой части ФЗ. Для разных ФЗ m может изменяться. Алгоритм for i:=1 to n do // цикл по всем ФЗ { m:=m(X[i]); // подсчет количества атрибутов в левой части for j:=1 to m do // цикл по всем атрибутам {Left_Part:= X[i][j]; // выбор одного из атрибутов for k:=1 to n do // цикл по всем ФЗ // если условие выполняется, то возможно наличие кольцевой структуры {if Left_Part == Y[k] then //функция проверяет множество S на наличие ВФЗ между X[i][j] и Y[i] при условии X[i]- X[i][j] call function_1(Left_Part, Y[i], X[i]- X[i][j]); Restore S, n; //восстановление полного списка ФЗ } } } //функция проверяет множество S на наличие ВФЗ между Left_Part и Right_Part при условии Usl function_1(Left_Part, Right_Part, Usl) for i:=1 to n do // цикл по всем ФЗ { if (Right_Part I X[i]) then //если правый атрибут входит в левую часть какой-либо ФЗ { Usl:=Usl+ X[i] - Right_Part; // то условие дополняется другимитами из левой части if (Left_Part == Y[i]) then //если произошло закольцевание { Add «Usl | Left_Part ~ Right_Part» //добавляется новая УВФЗ delete X[i]®Y[i]; //данная ФЗ удаляется из S n:=n-1; //количество ФЗ уменьшается } else //иначе осуществляется рекурсивный вызов для дальнейшего поиска { Right_Part := Y[i]; delete X[i]®Y[i]; //данная ФЗ удаляется из S n:=n-1; //количество ФЗ уменьшается function_1(Left_Part, Right_Part, Usl); } } } Выводы:
Автор пытается акцентировать внимание на вопросах ВФЗ. Если читатель имеет какую-либо информацию по данному вопросу, а также возражения, замечания или дополнения, присылайте их по адресу fil@ics.bmstu.ru. Литература:
|
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 АНДРЕЙ ФИЛИППОВИЧ
АНДРЕЙ ФИЛИППОВИЧ