 |
|
|
|
Программное приложение кластеризации данных
Программное приложение кластеризации данных Рассматривается технология создания веб-ресурса, реализующего алгоритмы кластерного анализа с максимально простым и понятным пользовательским интерфейсом, а также возможностью дальнейшего расширения выполняемых функций. Описываются структура и алгоритм работы такого приложения. Результат работы продемонстрирован на примере В современной жизни человек постоянно сталкивается с необходимостью анализа совокупностей объектов, будь то некие наблюдения, результаты опытов или характеристики объектов. Полученные данные необходимо обработать и систематизировать. Особенно сложно это сделать, если исследователь не знает точно, на какие группы надо разбить объекты, сколько их и надо ли вообще разбивать. В таком случае на помощь приходит кластерный анализ. Он представляет собой инструментарий для группировки многомерных объектов, основанный на представлении результатов отдельных наблюдений точками подходящего геометрического пространства с последующим выделением групп как «сгустков» этих точек (кластеров, таксонов). Данный метод исследования получил развитие в последние годы в связи с возможностью компьютерной обработки больших баз данных. Кластерный анализ предполагает выделение компактных, удаленных друг от друга групп объектов, отыскивает «естественное» разбиение совокупности на области скопления объектов. В настоящее время кластерный анализ применяется во многих сферах деятельности человека: в маркетинге, менеджменте, медицине, социологии, информатике и других [4]. Преимущество данного метода заключается в том, что он работает даже тогда, когда данных мало или не выполняются требования нормальности распределений случайных величин и другие требования классических методов статистического анализа [1, 4]. Программная реализация алгоритмов кластерного анализа на сегодняшний день разнообразна. Большинство статистических пакетов предоставляет такую возможность, однако имеет один существенный недостаток – они требуют специальных знаний для реализации разбиения. Но и совершать такие операции вручную необоснованно сложно и долго. Таким образом, возникает необходимость разработки приложения, которое реализует алгоритмы кластерного анализа и предоставляет их результаты в наглядном виде, но при этом нетребует от пользователя специальных знаний и имеет понятный интерфейс. Например, наличие у подобного приложения веб-интерфейса сделает его максимально доступным дляпользователей. В связи с этим реализация алгоритмов кластерного анализа для обработки многомерных данных в форме веб-ресурса является актуальной задачей. Формальная постановка задачи кластеризации следующая. Пусть X – множество объектов, Y – множество номеров (имен, меток) кластеров. Задана функция расстояния между объектами ρ(x, x'). Имеется конечная обучающая выборка объектов Xm = {x1, ..., xm} ⊂ X. Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике ρ, а объекты разных кластеров существенно отличались. При этом каждому объекту xη ∈ Xm приписывается номер кластера yη. Алгоритм кластеризации реализует построение функции a: X → Y, которая любому объекту x ∈ X ставит в соответствие номер кластера y ∈ Y. Множество Y внекоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров с точки зрения того или иного критерия качества кластеризации [1]. При написании программного приложения актуальной задачей является выбор языка программирования. Однако в настоящее время этот выбор не является очевидным. Практически все современные языки программирования высокого уровня приспособлены для решения сложных задач. При этом у них имеются достаточно серьезные отличия. Некоторые производят вычисления быстрее, некоторые медленнее. Для некоторых существуют уже готовые решения тривиальных подзадач. Предсказать заранее, какой язык будет лучше длярешения той или иной задачи, достаточно проблематично. Но существует ряд параметров, по которым можно оценить каждый из современных языков и подобрать оптимальный. При написании программного веб-приложения стоит задача подобрать такой язык программирования, который будет отвечать следующим требованиям:
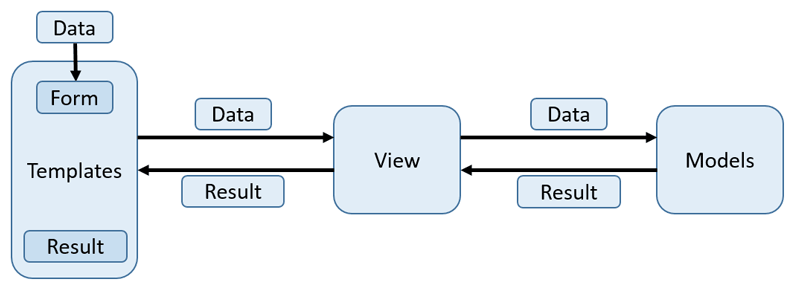
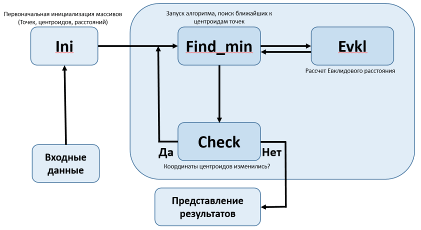
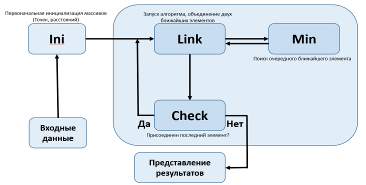
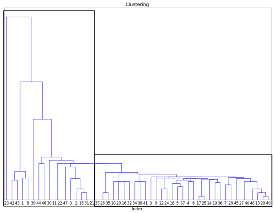
Исходя из данных требований основными претендентами для написания студенческих работ являются Java, C++, Python, PHP. Проанализировав соответствие указанных технологий требованиям задачи, был выбран язык программирования Python. Он обладает широким набором мощных библиотек для решения достаточно сложных математических задач, имеет возможности для визуализации (построение графиков, схем), а также свой собственный фреймворк Django, который существенно упрощает разработку веб-приложений [2, 3, 6]. При написании программного приложения были использованы следующие библиотеки: Matplotlib (для визуализации данных средствами двумерной (2D) и трехмерной (3D) графики), NumPy (реализует поддержку больших многомерных массивов и матриц, вместе с большой библиотекой высокоуровневых математических функций для операций с этими массивами), SciPy (содержит модули для решения задач оптимизации, интегрирования, обработки специальных функций, сигналов, изображений, генетических алгоритмов, решения обыкновенных дифференциальных уравнений и других задач), Django (позволяет увеличить скорость решения однотипных задач, возникающих при разработке веб-приложений) [4]. В основе принципов работы созданного веб-приложения лежат правила работы фреймворка Dhango. Он основан на широко распространенной модели программных приложений MVC (Model, View, Controller), которая позволяет легко вносить изменения в одну конкретную часть приложения без изменения остальных частей (см. рис. 1).
Рисунок 1. Модель MVT Основные файлы, обеспечивающие работу данного приложения, условно разбиты на три блока: Model, Template, View (см. рис. 1). Блок Model содержит стандартный файл models.py, который автоматически создается в любом Django-проекте, а также файл k_means_app.py, в котором прописаны все основные процедуры для процесса кластеризации данных. В этом блоке происходят обработка данных и возвращение результатов работы в блок View. Блок View содержит стандартный файл views.py, в котором описан алгоритм выполнения действий, необходимых для загрузки данных, рендера шаблонов пользовательского интерфейса, представления результатов работы программы. Блок Template включает несколько файлов, которые являются шаблонами и представляют собой модифицированные html-документы – main.html и some_template.html. Первый служит для отображения начальной страницы, где представлены некоторые общие сведения о кластеризации, форма для ввода данных, а также требования к ним. Второй же необходим для отображения результатов работы алгоритмов. Созданное веб-приложение содержит программную реализацию двух методов кластерного анализа: алгоритма к-средних и иерархического агломеративного алгоритма. В качестве входных данных для алгоритмов выступает двумерный массив из n записей, содержащий в себе пользовательские данные. Данный массив передается в процедуры из блока Views, где он был получен из пользовательского Excel-файла с помощью стандартной процедуры языка Python xlrd. Схема работы алгоритма к-средних представлена на рис.2. Он позволяет разбить исходное множество на группы, в каждой из которых находятся максимально «похожие» объекты. Сами группы при этом должны быть как можно «дальше» друг от друга. Мерой для определения наиболее схожих объектов является евклидово расстояние, для вычисления которого служит процедура evkl (k,p), где k – порядковый номер центра кластера, до которого вычисляется расстояние от точки с порядковым номером p.
Рисунок 2. Схема работы алгоритма к-средних В начале работы алгоритма происходит инициализация данных. Создается массив центроидов, расстояний между объектами и центрами кластеров, ближайших к точке центроидов. Заполняется массив объектов – tochki. В качестве центроидов в данной реализации алгоритма выбираются первые k точек. После этих действий алгоритм готов к запуску итераций, все основные действия которых происходят в процедуре find_min(). Первым шагом итерации является нахождение ближайших к центроидам точек. Для этого заполняется массив евклидовых расстояний mas_rasst при помощи процедуры evkl. Затем для каждой точки определяется ближайший кластер и записывается в массив mas_min. Следующим шагом является перерасчет координат центроидов как среднее принадлежащих им точек. Для этого служит массив sr_znach. Первые две записи каждого из его элементов служат для суммирования соответствующих координат точек, последняя представляет собой общее количество дочерних объектов. Итоговые координаты центроидов являются результатом простых вычислений: каждое из первых двух чисел разделить на значение, содержащееся в третьей ячейке. Если в результате работы полученные новые координаты центроидов (sr_znach) отличаются от старых (centri), то алгоритм запускается заново, иначе результат получен. Дляпроверки этого условия служит процедура check(). Кроме описанных основных процедур в составе реализации этого алгоритма, есть еще несколько вспомогательных. Это процедура main(), из которой происходит запуск итераций, процедура gmain(), которая служит для визуализации результатов работы программы, а также процедура res(), которая необходима для оценки качества проведенной кластеризации. Она вычисляет коэффициенты межкластерного и внутрикластерного расстояний, которые были упомянуты в разделе описания алгоритма кластерного анализа. Схема работы иерархического агломеративного алгоритма представлена на рис. 3. В отличие от к-средних он не является итеративным, выполняется до того момента, пока неостанется один кластер, с учетом того, что изначально каждый объект считается отдельным кластером.
Рисунок 3. Схема работы иерархического алгоритма Первым шагом алгоритма является заполнение матрицы расстояний между объектами – mas_rasst. Мерой расстояния, как и в к-средних, является евклидово расстояние. Для еговычисления применяется процедура evkl(i,j), где i,j – номера элементов, между которыми вычисляется расстояние. Далее в процедуре none() выбираются два элемента сминимальным расстоянием (процедура minimum()), которые еще не находятся в одной группе, и происходит объединение тех кластеров, которым они принадлежат. Алгоритм выполняется до тех пор, пока все объекты не будут объединены. У данного алгоритма также существуют вспомогательные процедуры. Check() проверяет, не находятся ли выбранные объекты в одном кластере. Процедура main() служит длязапуска всех основных шагов алгоритма. Процедура dendogram() нужна для визуального представления результатов работы программы. Реализованное программное приложение использовано для кластеризации множества клиентов банка. Из общей таблицы, содержащей сведения о клиентах банка, была сформирована выборка из 50 записей, для которых известны данные о текущей сумме их кредита и ежемесячном доходе. У банка имеется несколько предложений по выдаче кредитных карт, которые отличаются предлагаемой суммой. Задача заключается в разбиении множества клиентов на несколько групп, каждой из которых будет соответствовать наиболее подходящее кредитное предложение. Для запуска алгоритмов кластерного анализа необходимо запустить приложение и выбрать Excel-файл с исходными данными, определить количество кластеров для алгоритма к-средних в соответствующем поле ввода и нажать кнопку «Загрузить». Произойдет запуск алгоритма, после чего посетителя перенаправят на страницу с итогами. Первое изображение на данной странице представляет дендограмму – результат работы иерархического агломеративного алгоритма. Это изображение имеет один существенный недостаток– чем больше объектов были выбраны для анализа, тем менее читаемая схема получается на выходе. Эта проблема может быть решена в дальнейшем специальным форматным выводом дендограммы. В нашем примере иерархическая кластеризация пятидесяти объектов предоставляет в результате приемлемое изображение (см. рис. 4).
Рисунок 4. Иерархический кластерный анализ В данном случае на изображении с результатами иерархического кластерного анализа достаточно четко выделяются две группы объектов (см. рис. 4). Это позволяет сделать вывод отом, что «естественным» разбиением данного массива объектов является разбиение на два кластера, но данное утверждение нужно проверить. Для этого необходимо запустить программу несколько раз с тем же файлом данных, меняя вводимое значение в поле «количество кластеров» от двух до пяти и фиксируя параметры оценки качества кластерного анализа, результаты которых приведены в таблице 1. Таблица 1. Коэффициенты оценки качества кластеризации
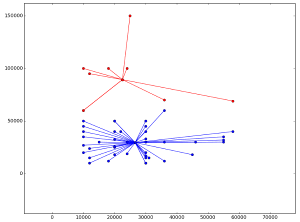
Как уже говорилось выше, качество кластерного анализа тем лучше, чем больше межкластерное расстояние и чем меньше внутрикластерное расстояние. Их частное при этом должно быть максимальным. Таким образом, наиболее качественным разбиением исходного множества является разбиение на пять кластеров. Однако требуемое разбиение на две группы обладает максимальным средним межкластерным расстоянием, а значит, также возможно для использования. На изображении (см. рис. 5) отчетливо видны как минимум два элемента, которые были причислены ко второму кластеру, однако они достаточно близки и к первому. Еще один элемент второго кластера лежит вотдалении от его центра. Похожие элементы есть и у первого кластера.
Рисунок 5. Разбиение методом к-средних на два кластера Разбиение исходного множества на пять групп визуально выглядит более естественно (см. рис. 6), каждый из кластеров обособлен и не имеет элементов со спорной принадлежностью, что может служить подтверждением полученных результатов оценки качества кластерного анализа.
Рисунок 6. Разбиение методом к-средних на пять кластеров Однако задачей стояло разбиение множества на две группы, а значит, анализировать необходимо именно результаты кластерного анализа методом k-средних с k=2. По условию поставленной задачи у банка имеется два предложения по кредитным картам, которые отличаются предлагаемой суммой кредита. При этом у клиентов уже имеются кредиты нанекоторую общую сумму, отмечаемую по оси абсцисс. Ось ординат показывает среднемесячный доход каждого клиента. Изучая результаты кластерного анализа, можно отметить, что в первой группе находятся те клиенты, у которых низкий среднемесячный доход или средний доход, но большая сумма текущего кредита. Этим клиентам банку нецелесообразно предлагать дополнительные кредитные карты с большой суммой. Второй кластер содержит в себе клиентов с высоким среднемесячным доходом или средним доходом и небольшой текущей суммой кредита. Таким клиентам банк может предложить дополнительные кредитные карты на определенных выгодных условиях. Однако есть по крайней мере один объект, который был отнесен в первый кластер, но при этом имеет высокую сумму текущего кредита и средний доход, его оттуда следует исключить. Итоговый список принадлежности клиентов кластерам:
Таким образом, была решена задача разбиения множества, состоящего из пятидесяти клиентов на две максимально однородных группы. Однако необходимо отметить, что данное решение не является единственным и может меняться в зависимости от выбора начальных точек, метрики и ряда других параметров. Необходимо отметить, что реализованное программное приложение не связано с какой-либо конкретной предметной областью. Основным требованием к входным данным является их четко определенная структура. Поэтому приложение может быть использовано в любых сферах деятельности, где необходимо решить задачу разбиения на группы. Приложение позволяет проводить кластерный анализ больших массивов данных без использования крупных пакетов анализа данных, которые, кроме высоких требований кспециальным знаниям, также обладают достаточно серьезной стоимостью. Разработанное приложение, в свою очередь, предоставляет сервис для кластеризации на бесплатной основе в веб-интерфейсе и имеет, конечно, несколько другую аудиторию, которая ранее не была охвачена существующими сервисами. Также стоит отдельно отметить язык реализации Python. Реализованное приложение, конечно, имеет массу возможностей для расширения – начиная от увеличения размерности входных данных, заканчивая добавлением новых алгоритмов как кластеризации, так и вообще анализа данных. Средства языка Python в связке с фреймворком Django позволяют производить подобную модернизацию.
Ключевые слова: кластерный анализ, язык программирования Python, иерархический алгоритм, алгоритм k-means, программное приложение кластеризации данных. Software application for data clustering Buchatskaya V.V. Candidate of Technical Sciences, Associate Professor of Department of Applied Mathematics, Information Technology and Information Security. Adyghe State University, Maikop. buch_vic@mail.ru Buchatskiy P. Yu. Candidate of Technical Sciences, Head of Department of Automated Systems of Processing Information and Control. Adyghe State University, Maikop. butch_p99@mail.ru Gushchin K.A. Undergraduate student. Adyghe State University, sargos92@gmail.com Abstract: Consider the technology for creating web-resource, implements cluster analysis algorithms with the most simple and intuitive user interface, and possibility of further expansion of the functions. Describe structure and algorithm of this application. Result of the work is demonstrated by this example. Keywords: cluster analysis, the Python programming language, the hierarchical algorithm, k-means algorithm, software, data clustering application. |
БУЧАЦКАЯ В.В., к.т.н., доцент, доцент кафедры прикладной математики, информационных технологий и информационной безопасности Адыгейского государственного университета, 
БУЧАЦКИЙ П.Ю., к.т.н., доцент, заведующий кафедрой автоматизированных систем обработки информации и управления Адыгейского государственного университета, 
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
