 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Влияние запаздывания сигналов в виртуальном сетевом пространстве на точность и устойчивость систем автоматического управления
Влияние запаздывания сигналов в виртуальном сетевом пространстве В статье показано, что в типовой системе автоматического управления, содержащей сетевую компоненту, возможно значительное падение точности регулирования за счет сетевого запаздывания. Рассмотрен случай компенсации запаздывания с помощью неточной модели запаздывания в случае, когда модель самого объекта управления считается достаточно точной. Показано, что возможно появление таких провалов частотной характеристики при компенсации Современные распределенные системы управления реального dhtvtyb функционируют в виртуальном сетевом пространстве, что накладывает существенный отпечаток на динамику процессов в них. Запаздывание при распространении сигналов в таком пространстве является практически неизбежным злом, с которым приходится считаться и бороться. Особенно значительных величин это запаздывание достигает при использовании большого числа маршрутизаторов и связанного с этим буферирования. Основной особенностью систем управления с наличием сетевого компонента Ethernet является то, что этот компонент вносит дополнительное запаздывание, влияющее на качество переходных процессов. Таким образом, эти системы являются системами с запаздыванием. Классы сетевого QoS, задающие ограничения для значений рабочих характеристик сети, приведены в таблице 1 [1]. Таблица 1. Классы QoS
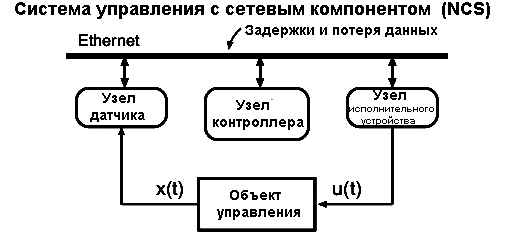
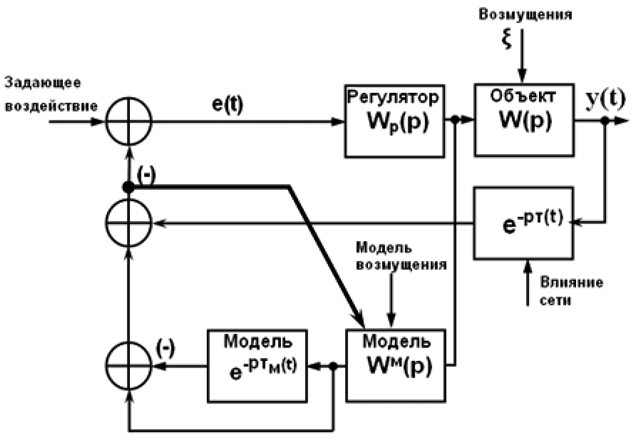
Таким образом, не гарантируется время задержки менее 0,1 с в сети Ethernet даже в рамках использования сервиса QoS. Таково реальное положение дел, и оно означает, что приналичии сетевой компоненты затруднительно управлять объектом с характерной постоянной времени ~ 0,1 c и менее. Кроме того, такое запаздывание обычно является переменным, но в данной статье будет нами рассмотрен эффект, не связанный с переменностью времени запаздывания, авозникающий при плохо определенном (недостаточно точно известном) времени запаздывания. В таком контексте обычно либо используют экстраполятор функций на время запаздывания, либо встроенную модель объекта управления с запаздыванием [2]. Причем оба этих подхода плохо работают при неточно известном запаздывании. Будем предполагать (это реалистично), что выход объекта без запаздывания физически получен быть не может, поэтому будем предполагать наличие в системе компенсации запаздывания (см. рис. 1).
Рисунок 1. Типовая распределенная система автоматического управления Ограничимся случаем линейной системы с постоянными коэффициентами, так как даже в такой системе рассмотренный ниже эффект проявляется в полной мере. Пусть W(p)рег, W(p)о и W(p)ос – соответственно передаточные функции регулятора, объекта управления и обратной связи. Передаточная функция разомкнутой системы:
(и соответствующая частотная характеристика W(jω)рc определяет величину ошибки слежения в системе по следующей формуле [2]:
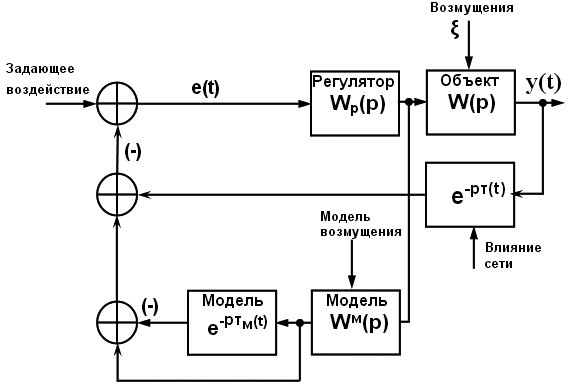
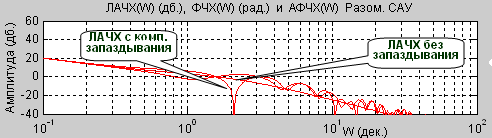
В частотной области получим оценку спектральных составляющих ошибки, поэтому стремятся к тому, чтобы |W(jω)рc| - 1 < ε – требуемой точности системы. Будем предполагать, что это требование выполнено, если отсутствует (поэтому и не учитывается) запаздывание. Теперь введем компенсацию запаздывания, для чего добавим в систему модели объекта, помехи и, наконец, запаздывания, которые входят в виде программных модулей в ПО регулятора. Мы не можем заранее предполагать, что все эти модели точны, кроме того, помеха может иметь стохастическую природу и поэтому точно не воспроизводится. Будем дляопределенности считать, что модель объекта достаточно точна, а вот модель запаздывания отличается от реального запаздывания. Все это отражено на рис. 2.
Рисунок 2. Компенсация запаздывания Очевидно, если модель запаздывания точна, то происходит его (запаздывания) полная компенсация и ЛАЧХ разомкнутой скомпенсированной системы не отличается от ЛАЧХ системы вообще без запаздывания. Но, к сожалению, точная компенсация невозможна. Типичный вид логарифмической амплитудно-частотной характеристики (ЛАЧХ) такой системы (в разомкнутом виде) приведен ниже (см. рис. 3).
Рисунок 3. ЛАЧХ разомкнутой системы без запаздывания и с последующей неточной компенсацией запаздывания ЛФЧХ, проходя на достаточно высоком уровне, обеспечивает малую ошибку (в соответствии с формулой (2)). Этот эффект хорошо виден на рис. 3, где приведено несколько случаев неточной компенсации запаздывания. В некоторых случаях провалы ЛАЧХ достигают -60 дб, но это наблюдается далеко не всегда. Точными нулями будут частоты, удовлетворяющие уравнению:
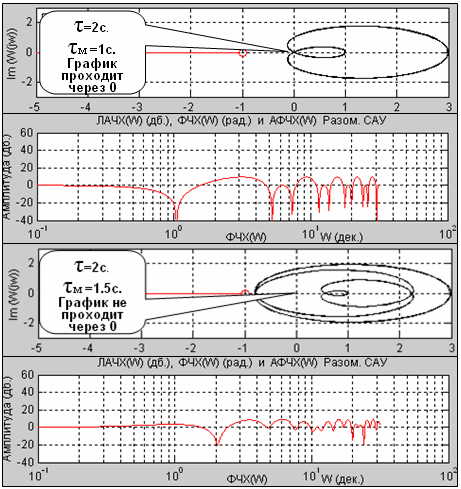
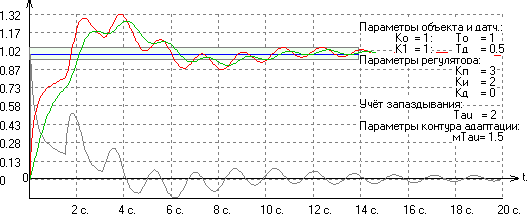
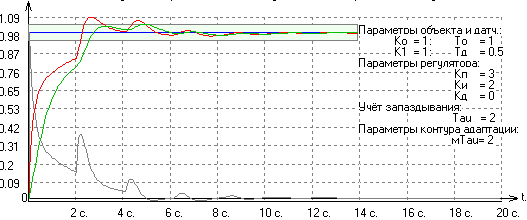
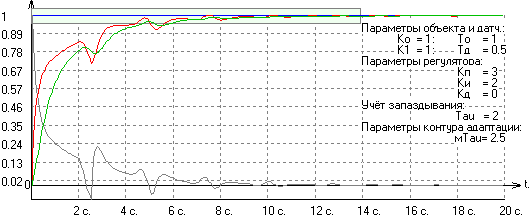
Наличие или отсутствие корней этого уравнения связано с соотношением между τ и τм. Если эти числа рационально соизмеримы (n·τ = m·τм), то (3), являясь в этом случае периодической функцией, может иметь решение, но может и не иметь. Примеры приведены на рис. 4. Здесь отображен годограф F(ω) [2] при неотрицательных частотах на комплексной плоскости. Обращать внимание следует на прохождение годографа вблизи точки 0. Также приведены графики ЛАЧХ этой функции (по оси ординат – децибелы).
Рисунок 4. Случай соизмеримых запаздываний: годографы F(ω) и соответствующие ЛАЧХ Очевидно, что имеются глубокие провалы ЛАЧХ на некоторых частотах, препятствующие высокой точности замкнутой САУ. При этом при точной компенсации запаздывания таких провалов нет (так же, как и в системе без запаздывания). Ниже на рис. 5-7 приведены переходные процессы в этой системе при различной степени компенсации запаздывания.
Рисунок 5. Переходный процесс при τ = 2 и τм = 1.5
Рисунок 6. Переходный процесс при τ = 2 и τм = 2
Рисунок 7. Переходный процесс при τ = 2 и τм = 2.5 Поэтому даже малое изменение параметров модели запаздывания может оказать сильное влияние на точность системы на некотором множестве частот. Если эти частоты лежат вне рабочего диапазона, то это не оказывает существенного влияния. В противном случае качество работы системы автоматического управления ухудшается. Выходом из этого положения была бы более точная модель запаздывания в сетевой компоненте, что труднореализуемо в силу того, что само это запаздывание может меняться очень динамично и в широких пределах. Целесообразно будет рассмотреть два крайних случая реализации системы с компенсацией запаздывания в сетевой компоненте:
где новая текущая оценка времени запаздывания в модели запаздывания вычисляется через градиент целевой функции с текущим шагом. Уточнить текущий шаг можно через матрицу вторых частных производных (метод Ньютона) или воспользоваться иным (менее точным) методом выбора этого шага. Важно, чтобы процедура (4) достаточно быстро сходилась к истинному значению запаздывания.
Рисунок 8. Компенсация запаздывания с адаптацией
Ключевые слова: распределенная система управления, запаздывание, компенсация. The influence of the delay of the signals in the virtual network space on the accuracy and stability of automatic control systems Tumanov M.P., Cand. of Techn. Sciences, professor (MIEM HSE), Moscow, mtunanov@hse.u Abstract: The article shows that in a typical automatic control system that contains the network component may be a significant drop in control accuracy due to network lag. The article describes a case of lag compensation using inaccurate delay model in the case when the model of the control object is considered sufficiently accurate. It is shown that the possible emergence of such dips of the frequency response with compensation. Keywords: distributed control system, delay compensation. |
||||||||||||||||||||||||||||||||||||||||||||
ТУМАНОВ М.П., к.т.н., профессор (НИУ ВШЭ, МИЭМ), Москва, 
(1)
(2)
(3)
(4)
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
