|
|
|
|||||||||||||
|
|
Оптимальное управление распространением вирусов: В работе рассматривается задача управления для SIR-модели эпидемий с переменным количеством узлов. Изучается задача минимизации затрат для модели SIR, управлениями вкоторой выступают «вакцинация» и «лечение» узлов. Исследуются два различных функционала и обсуждаются их особенности. На основе принципа максимума Понтрягина получена структура оптимального управления для каждого функционала. Найдены численные решения с использованием методов пристрелки и Рунге-Кутта 4-го порядка. Исследуется зависимость решения от параметров задачи Одним из основных подходов к изучению процесса заражения компьютерной сети вирусом является использование математических моделей, аналогичных моделям распространения вируса среди населения. Существуют различные модели эпидемий, применимые для людей, они могут учитывать, например, инкубационный период для вируса, появление естественного иммунитета, естественную смертность и рождаемость индивидуумов. Использование этих моделей для исследования заражения компьютерных сетей накладывает свой отпечаток, например для компьютера невозможно появление естественного иммунитета, подобные особенности нужно учитывать при применении математических моделей и их модификаций. В связи с тем, что математические модели распространения вирусов описываются системами нелинейных дифференциальных уравнений, многие результаты удается получить только численно. Компьютерное моделирование очень часто проводят с использованием пакета Matlab [1]. Однако следует иметь в виду, что одной из проблем при моделировании процессов заражения остается не выбор среды, где будет проходить моделирование, а корректность поставленной задачи и выбора способа решения. В настоящей работе рассматривается SIR-модель. В данной модели узлы в сети делятся на три группы:
Предполагается, что период функционирования системы достаточно мал, так что установленный антивирус не успевает устаревать. Мы рассматриваем однородную сеть, то есть каждый узел может установить контакт с любым узлом сети, количество узлов в сети не меняется [6]. Такая модель описывается следующими уравнениями:
Здесь:
В данной работе рассматривается модель SIR с возможностью «вакцинирования», а именно предполагается, что, кроме «лечения» зараженных, т.е. удаления на них вирусов иустановки антивирусной программы, имеется возможность установки антивирусной программы на незараженные (Восприимчивые) узлы. Обозначим:
Кроме того, добавим условие, что под действием вируса узлы выходят из строя с интенсивностью α. Тогда процесс распространения вирусов в сети можно описать следующими дифференциальными уравнениями:
Ниже мы перечислим лишь некоторые недавние результаты, которые были получены для аналогичной модели. В [1] изучается модель SIR. Особенность этой работы в том, что в модели учитывается, что количество узлов в системе может меняться: появляются новые узлы, выходят из строя старые узлы. В работе проведен анализ устойчивости решений. В [2] модель SIR применяется для исследования распространения ВИЧ-инфекции. В работе доказана теорема о существовании оптимального решения, для поиска минимума функционала используется принцип максимума Понтрягина. Найдена структура оптимального управления. Выведенные уравнения решаются численно. На основе полученных данных был сделан вывод о том, что лечение и вакцинация очень существенно влияют на быстрое угасание эпидемии. Постановка задачи Мы будем рассматривать задачу оптимального управления для описанной выше модели: минимизировать функционал
на траекториях системы (1)-(3) с начальными условиями S(0) = S0, I(0) = I0, R(0) = R0. Функционалы такого вида типичны для задач управления распространением вирусов в сетях [1]-[2]. В этом функционале, с одной стороны, учитывается число «зараженных» узлов (и связанные с этим затраты), с другой стороны, затраты на «лечение» и «вакцинацию» узлов. В качестве управления рассмотрим параметры u1(t) и u2(t). Будем предполагать, что u1(t) и u2(t) – измеримые, ограниченные на отрезке [0;T] функции:
С использованием теоремы Филиппова [5] можно показать, что решение в задаче (1)-(5) существует. Заметим, что целевой функционал не зависит от переменной R, правая часть уравнений (1) и (2) также не содержит переменную R. Поэтому можно уменьшить размерность задачи, исключив из рассмотрения уравнение (3). Необходимые условия оптимальности Применим к задаче принцип максимума Понтрягина [3]. Запишем функцию Понтрягина:
Пусть (S*(t), I*(t)) − оптимальное решение в задаче (1)-(5), (u1*(t), u2*(t)) − соответствующие оптимальные управления. Тогда согласно принципу максимума Понтрягина найдутся постоянная λ0 ≥ 0 и кусочно-непрерывно дифференцируемая вектор функция ψ(t) = (ψ1(t), ψ2(t)), такие, что: 1) ψ(t) удовлетворяет системе дифференциальных уравнений:
2) Выполнены условия трансверсальности: ψ1(T) = 0, ψ2(T) = 0 3) Выполнено условие максимума для функции H:
Заметим, что для данной задачи λ0 ≠ 0. В дальнейшем положим λ0 = 1. Анализ условия максимума Рассмотрим подробнее условие максимума:
Выпишем отдельно слагаемые с управлением u1 и управлением u2.
Функции F(u1) и G(u2) являются вогнутыми, следовательно, максимум достигается в стационарных точках функции F и G, если эти точки являются допустимыми. Если стационарная точка не является допустимой, то минимум надо искать на границе области. Найдем стационарные точки функций F и G.
Отсюда:
Получаем следующую структуру оптимального управления:
Заметим, что в силу условий трансверсальности управления в заключительный момент времени Т равны 0: u1*(T) = u2*(T) = 0. Алгоритм численного решения задачи Выпишем систему уравнений принципа максимума Понтрягина:
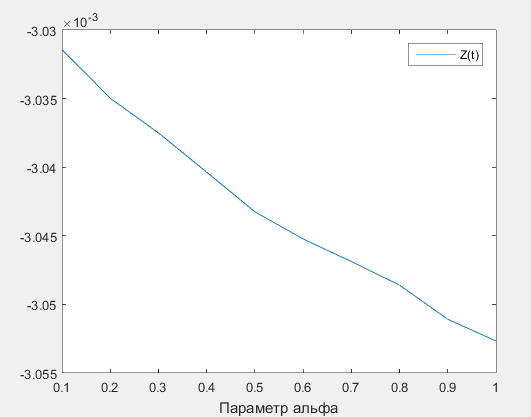
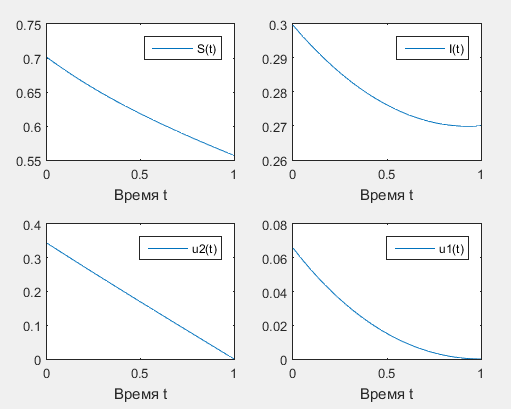
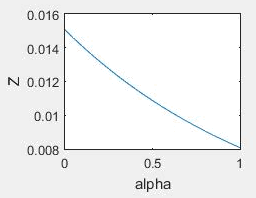
где u1(t), u2(t) определяются из (6), (7). Имеем следующие краевые условия для системы (8): S(0) = S0, I(0) = I0, ψ1(T) = 0, ψ2(T) = 0 Таким образом, мы перешли от задачи оптимального управления к краевой задаче для системы четырех дифференциальных уравнений первого порядка. При интегрировании получим 4 неизвестных постоянных интегрирования, для определения которых есть 4 начальных условия. Для численного решения краевой задачи принципа максимума будем применять итерационный процесс − метод стрельбы, который заключается в последовательном решении задач Коши. Для решения задачи Коши применим метод Рунге-Кутты 4-го порядка. Система (8) решается численно в обратном времени начиная с момента Т. Задаются некоторые начальные условия S(T) и I(T). Затем задача Коши для системы уравнений сначальными условиями на правом конце решается численно и сравниваются полученные S(0) и I(0) с заданными, если они совпали с нужной нам точностью, то процесс завершается, если нет, то процесс повторяется с новыми S(T) и I(T), вычисленными по особому правилу [4]. Влияние параметров на оптимальные решения Анализ зависимости оптимального значения функционала от параметров задачи выявил следующую особенность: с ростом α (интенсивность фатального выхода из строя узлов поддействием вируса) оптимальное значение функционала уменьшается. Хотя интуитивно ясно, что интенсивный выход из строя узлов должен играть «отрицательную» роль. Очевидно, что такое влияние параметра α на функционал не является адекватным. Таким образом, нужно изменить функционал так, чтобы на оптимальном решении уменьшить число сломанных узлов и увеличить число восстановленных узлов. Рисунок 1. Оптимальные решения системы при значениях α = 0.1, β = 0.75, С1 = 1, С2 = 0.4, С3 = 0.5, T = 1 Рисунок 2. Зависимость функционала от параметра α Задача максимизации числа восстановленных узлов с учетом затрат Рассмотрим следующую задачу оптимального управления: минимизировать функционал:
на траекториях системы:
с начальными условиями: S(0) = S0, I(0) = I0, R(0) = R0, и ограничениями на управления (5). Запишем функцию Понтрягина:
Пусть (S*(t), I*(t), R*(t)) − оптимальное решение в задаче, − оптимальное управление. Тогда согласно принципу максимума Понтрягина найдутся постоянная λ0 ≥ 0 икусочно-непрерывно дифференцируемая вектор-функция ψ(t) = (ψ1(t), ψ2(t), ψ3(t)), такие, что: 1) ψ(t) удовлетворяет системе дифференциальных уравнений:
2) Выполнены условия трансверсальности: ψ1(T) = 0, ψ2(T) = 0, ψ3(T) = 0 3) Выполнено условие максимума для функции H:
Заметим, что в данной задаче также можно положить λ0 = 1. По аналогии с предыдущим случаем найдем структуру оптимального управления.
Алгоритм численного решения задачи Выпишем систему уравнений принципа максимума Понтрягина:
где u1(t), u2(t) определяются из (10), (11). Краевые условия для (12): S(0) = S0, I(0) = I0, ψ1(T) = 0, ψ2(T) = 0, ψ3(T) = 0. Из этих условий можно сразу аналитически найти ψ3(t) = C0(T – t). Строим численное решение задачи сиспользованием метода пристрелки. Напомним, с предыдущим функционалом возникла проблема при увеличении параметра α − интенсивности выхода узлов из строя под действием вируса. Выясним, как функционал (8) и управления реагируют на изменения параметра α. На рис. 3 показана зависимость функционала от α. Видно, что с ростом α функционал уменьшается, как и предыдущий функционал, это означает, что и новый функционал (8) имеет тот же недостаток. Рисунок 3. Зависимость функционала от параметра α Заключение В работе изучается SIR-модель распространения вирусов в компьютерных сетях. Рассматриваются задачи управления для данной модели:
Для каждой из задач найдена структура оптимального управления. Найдены численные решения. Проведен анализ зависимости решений от параметров задачи. Показано, чторассматриваемые целевые функционалы имеют существенный недостаток − принимают лучшие значения при возрастании интенсивности поломки, что не отражает реальные цели пользователя. В дальнейшем предполагается построить функционал, который имеет «правильное» поведение, то есть уменьшается с ростом α.
Optimal control for virus spreading: analytical and numerical results Klimenkova O.D., Bachelor MIEM NRU HSE, Moscow «applied mathematics», odklimenkova@edu.hse.ru Abstract: In this work, optimal control problem for a SIR model with variable size of population is considered. Our goal is to solve a problem of costs minimization. We investigate a SIR model with «vaccination» and «treatment» as controls. We consider two different functional and discuss their characteristics. Structures of optimal control are defined for every functional. Pontryagin’smaximum principle is used to characterize the optimal levels of controls. The optimality system is solved numerically. Then we analyze the dependence of solutions on parameter of problems. The simulation results are discussed. Keywords: SIR-model, optimal control, Pontryagin’s maximum principle. |
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 КЛИМЕНКОВА О.Д., бакалавр МИЭМ НИУ ВШЭ, Москва, по направлению «прикладная математика»,
КЛИМЕНКОВА О.Д., бакалавр МИЭМ НИУ ВШЭ, Москва, по направлению «прикладная математика», 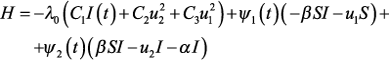
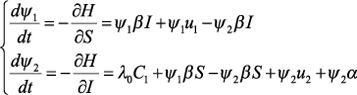
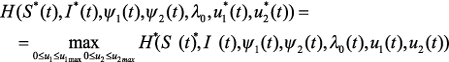
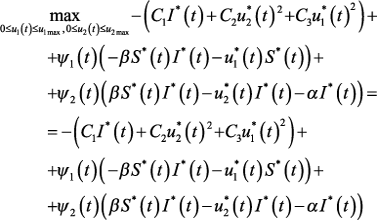
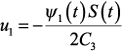 и
и 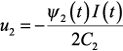
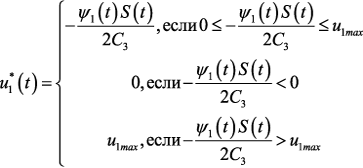 (6)
(6)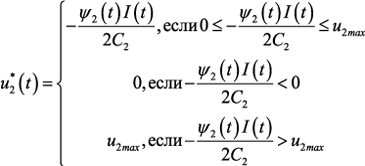 (7)
(7)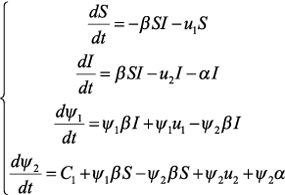 (8)
(8)
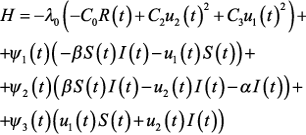
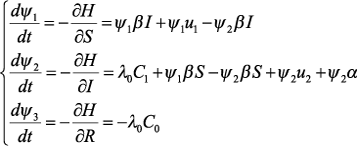
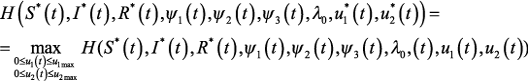
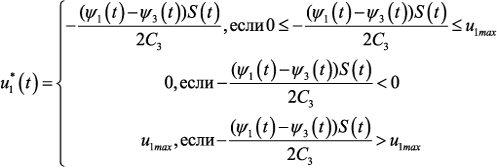 (10)
(10)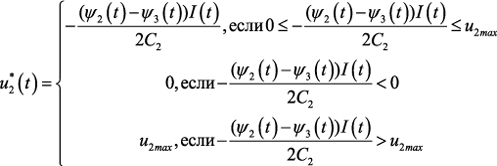 (11)
(11)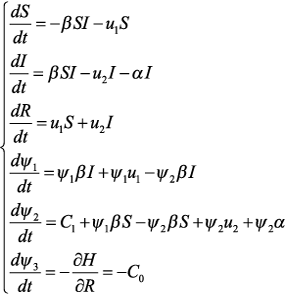 (12)
(12)