 |
|
|
|||||||||||||
|
|
Практическая реализация Рассматриваются реализации алгоритмов стохастической оптимизации на языке программирования высокого уровня Java Введение Одной из основных тенденций настоящего времени является всеобщая компьютеризация и информатизация, построение информационного сообщества. Растут потребности в вычислительных ресурсах, активно используются возможности проведения вычислений в распределенных средах (РС). При этом сами РС становятся объектами пристального внимания со стороны злоумышленников. Увеличивается число вирусных атак, несанкционированных вторжений. Любая такая атака или вторжение может привести к серьезным потерям, нанести вред человеческим жизням и здоровью, значительным затратам на ликвидацию последствий, восстановлению важной информации и прочему. Очевидным становится необходимость контроля и усиления защиты. Рассматривается узел РС как система массового обслуживания (СМО). У этой СМО имеется определенная производительность обработки заявок (заданий для вычислений). На вход узла поступают полезные достоверные заявки изнадежных источников и вредные заявки от злоумышленников. Интенсивности от надежных источников априори известны, потоки заявок стационарны. Интенсивности заявок от злоумышленников, атакующих узел, априори неизвестны, потоки нестационарны. По свойству простейшего потока заявок суммарная интенсивность входного потока заявок в узле есть простая сумма интенсивностей отдельных потоков, а результирующий поток является простейшим. Поскольку производительность обработки заявок может быть изменена в директивном порядке как администратором узла, так и специализированным программным обеспечением, удобно рассматривать узел как СМО типа M/G/1. Следует учесть, что, помимо затрат на устранение последствий, необходимо уменьшать затраты на контроль. Обобщая, задача получается громоздкой и аналитически не всегда и во всех случаях разрешимой. Поэтому необходимо разрабатывать специализированные структурные программно-аппаратные решения. Одним из путей решения могут стать разработка и исследование программно-инструментального комплекса, включающего в себя имитационные модели, сценарные модули обеспечения поддержки принятия решений и программные модули выбора вариантов. Целью настоящей работы является описание подхода к управлению узлом вычислительной системы с использованием средств выбора вариантов автоматными алгоритмами. Обзор особенностей применения методов стохастической оптимизации Достаточно хорошо известны возможности применения для управления дискретными объектами с конечным множеством управляющих воздействий [1, 2, 3] методов на основе автоматных алгоритмов для безусловной одномерной минимизации. В основе всех таких алгоритмов лежит использование рекуррентных последовательностей для формирования состояния автомата. Структура автомата задается вектором вероятностей выбора состояний, каждый изкомпонентов которого содержит вероятность пребывания автомата в соответствующем компоненту состоянии. Выбор следующего состояния осуществляется на основе этого вектора, в том числе и с использованием алгоритма половинного деления. При использовании автоматных алгоритмов время функционирования объекта проектирования разбивается на отрезки. Временная длительность этих отрезков одинакова. Каждому отрезку ставится в соответствие значение функции текущих потерь. В литературе описаны некоторые алгоритмы, их вектор-функции, иногда – способы реализации. При этом их можно разделить на две группы – беспроекционные и проекционные (иногда – беспроекторные и проекторные). Основным отличием беспроекционных алгоритмов от проекционных является использование в последних так называемого оператора проецирования (проектирования) на симплекс. В вектор-функции происходит пересчет компонентов вектора вероятностей выбора состояний, в том числе и с учетом значений текущих потерь. По этой причине беспроекционные алгоритмы могут во многих случаях функционировать только с бинарной функцией потерь. Напротив, использование оператора проецирования позволяет использовать в проекционных алгоритмах не только бинарную, но и небинарную ограниченную функцию текущих потерь. При этом в открытых источниках не рассматривается решение трудоемкой задачи программной реализации автоматных алгоритмов, нет применения к управлению отдельным вычислительным узлом РС. Используемые обозначения для описания рекуррентных соотношений Все рассматриваемые алгоритмы оптимизации используют правила формирования рекуррентных последовательностей. Пусть по [1]:
Беспроекционные алгоритмы используют соотношения pn+1 = pn – γn R(xn, pn, ξn). Проекционные алгоритмы – pn+1 = Разрабатывается средство поддержки принятия решений (СППР), использующее перечисленные выше методы. СППР имеет возможность неограниченного расширения по используемым методам стохастической аппроксимации сразличными рекуррентными функциями. Таким образом, учитывается системотехнический принцип развития, неопределенности и случайности. В дальнейшем во всех реализациях алгоритмов используется соответствие между обозначениями [1, 2] и идентификаторами по таблице 1, максимально близкое к обозначениям в программах Фортран-IV. Рекуррентные соотношения приводятся по [1]. Программные реализации одного шага алгоритмов оптимизации и вспомогательных подпрограмм С учетом принципов системного анализа разрабатывается программная система для безусловной минимизации средних потерь с использованием алгоритмов стохастической оптимизации. В таблицу 1 сводится описание реализованных алгоритмов с указанием вектор-функции. Алгоритм Нарендры-Шапиро. Алгоритм Нарендры-Шапиро предназначен для решения задач адаптивного выбора вариантов с бинарной функцией потерь. Рекуррентное соотношение и ограничения для аргументов приводятся в формуле (1). pn+1 = pn + γn (1 – ξn)(e(xn) – pn), ξn ∈ {0,1}, γn ∈ (0,1) (1) В листинге 1 приводится реализация алгоритма, идентификаторы аргументов метода и переменных соответствуют таблице 1. Листинг 1. Метод для реализации одного шага алгоритма Нарендры-Шапиро public static double algNarendryShapiro(double[] P, double GAM, int[] NV_v, int iter) { int N = P.length; int NV = autom(P); double CSI = poteri_binary(NV); if (CSI == 1.0) { return CSI; } for (int i = 0; i < N; i++) { if (i == NV) { P[i] = P[i] + GAM * (1.0 - P[i]); } else { P[i] = P[i] - GAM * P[i]; } } NV_v[iter] = NV; return CSI; }
Таблица 1. Соответствие обозначений
Алгоритм Льюса. Алгоритм Льюса предназначен для решения задач адаптивного выбора вариантов с бинарной функцией потерь. Рекуррентное соотношение и ограничения для аргументов приводятся в формуле (2).
В листинге 2 приводится реализация алгоритма, идентификаторы аргументов метода и переменных соответствуют таблице 1. Листинг 2. Метод для реализации одного шага алгоритма Льюса public static double algLuce(double[] P, double GAM, double A, int[] NV_v, int iter) { int N = P.length; int NV = autom(P); double CSI = poteri_binary(NV); double X; if (CSI == 1.0) { X = -GAM / (1.0 - (1.0 - A) * P[NV]); } else { X = GAM / (A + (1.0 - A) * P[NV]); } for (int i = 0; i < N; i++) { if (i == NV) { P[i] = P[i] + P[NV] * (1.0 - P[i]) * X; } else { P[i] = P[i] - P[NV] * P[i] * X; } } NV_v[iter] = NV; return CSI; } Алгоритм Варшавского-Воронцовой. Алгоритм Варшавского-Воронцовой предназначен для решения задач адаптивного выбора вариантов с бинарной функцией потерь. Рекуррентное соотношение и ограничения для аргументов приводятся в формуле (3).
В листинге 3 приводится реализация алгоритма, идентификаторы аргументов метода и переменных соответствуют таблице 1. Листинг 3. Метод для реализации одного шага алгоритма Варшавского-Воронцовой public static double algVarVor(double[] P, double GAM, int[] NV_v, int iter) { int N = P.length; int NV = autom(P); double CSI = poteri_binary(NV); double X; if (CSI == 1.0) { X = -GAM; } else { X = GAM; } for (int i = 0; i < N; i++) { if (i == NV) { P[i] = P[i] + P[NV] * (1.0 - P[i]) * X; } else { P[i] = P[i] - P[NV] * P[i] * X; } } NV_v[iter] = NV; return CSI; } Алгоритм Буша-Мостеллера. Алгоритм Буша-Мостеллера предназначен для решения задач адаптивного выбора вариантов с бинарной функцией потерь. Рекуррентное соотношение и ограничения для аргументов приводятся в формуле (4).
В листинге 4 приводится реализация алгоритма, идентификаторы аргументов метода и переменных соответствуют таблице 1. Листинг 4. Метод для реализации одного шага алгоритма Буша-Мостеллера public static double algBuMost(double[] P, double GAM, int[] NV_v, int iter) { int N = P.length; int N1 = N - 1; int NV = autom(P); double CSI = poteri_binary(NV); double X = CSI / N1; for (int i = 0; i < N; i++) { if (i == NV) { P[i] = P[i] + GAM * (1.0 - P[i] - CSI); } else { P[i] = P[i] + GAM * (P[i] - X); } } NV_v[iter] = NV; return CSI; } Алгоритм Назина-Позняка. Алгоритм Назина-Позняка предназначен для решения задач адаптивного выбора вариантов с ограниченной небинарной функцией потерь. Рекуррентное соотношение и ограничения для аргументов приводятся вформуле (5).
В листинге 5 приводится реализация алгоритма, идентификаторы аргументов метода и переменных соответствуют таблице 2. Листинг 5. Метод для реализации одного шага алгоритма Назина-Позняка public static double algStepPR(double[] P, double GAM, double EPS, double DEL, int[] NV_v, int iter) { double CSI; double S; int NV = autom(P); CSI = poteri(NV); S = (CSI - DEL) * GAM / P[NV]; P[NV] = P[NV] - S; System.arraycopy(proekNazinPoznyak(P, EPS), 0, P, 0, P.length); NV_v[iter] = NV; return CSI; }
Таблица 2. Результаты расчетов по формулам (5)
Необходимы еще некоторые служебные подпрограммы-методы. Оператор проектирования
Величина ε > 0 для обеспечения ненулевой вероятности выбора каждого варианта. В листинге 6 приводится реализация алгоритма проектирования Назина-Позняка. Листинг 6. Метод для реализации оператора проектирования public static double[] proekNazinPoznyak(double[] q, double e) { int N = q.length; double r = e * N; double ar = 1.0 - r; double ak = N; double sq1 = 0.0; double[] p = new double[N]; boolean[] mon = new boolean[N]; boolean shagAlgo = true; for (int i = 0; i < N; i++) { sq1 += q[i]; p[i] = q[i]; } sq1 = 1 - sq1; for (int i = 0; i < N; i++) { mon[i] = false; p[i] = (p[i] - e) / ar; } sq1 /= ar; while (shagAlgo) { shagAlgo = false; for (int i = 0; i < N; i++) { if (!mon[i]) { p[i] += sq1 / ak; } } for (int i = 0; i < N; i++) { if (!mon[i] && (p[i] < 0.0)) { sq1 = p[i]; p[i] = 0.0; mon[i] = true; ak--; shagAlgo = true; break; } } } for (int i = 0; i < N; i++) { p[i] = ar * p[i] + e; } return p; } Процедура выбора варианта методом половинного деления. Принимает единственный аргумент – одномерный массив вещественных чисел одинарной точности, задающий распределение вероятностей целочисленной случайной величины. Возвращает целое число – номер выбранного варианта от 1 до N. В листинге 7 приводится реализация метода. Листинг 7. Метод для реализации выбора варианта методом половинного деления public static int autom(double[] P) { int N = P.length; int N1 = N - 1; int NC = N1; double A = -randu(); for (int i = 0; i < N1; i++) { A += P[i]; if (A < 0) { continue; } else { NC = i; break; } } return NC; } Сценарное управление узлами сред. При сценарном управлении узлами РС необходимо учитывать следующее:
Необходимо поставить в соответствие каждому выходу стохастического автомата конкретное управляющее воздействие. Для этих целей полагается, что выходу автомата соответствует единичное значение, если узел РС подключен к РС, инулевое значение, если отключен. Некоторые современные системы организации обмена сообщений и обеспечения хранения их очередей, имеют для этого встроенные механизмы изоляции узлов и переключения узлов. При этом наиболее полной доступной метрикой является текущая длина очереди заявок в узле. Конечно, для практического использования и построения функции штрафов текущей длины очереди недостаточно. Необходима оценка значений важнейших системных характеристик, таких как среднее число заявок в узле, среднее число заявок в очереди, среднее время обработки заявки, среднее время простоя и некоторые другие. С помощью построения функции текущих потерь на основе взвешенной централизованной суммы можно организовать процедуру выбора вариантов. Независимо от способа целевой реализации следует различать возможности автоматического и автоматизированного управлений. В первом случае ЛПР не принимает участия в работе программно-аппаратного комплекса, во втором – влияет на характер корректировки, ее глубину и полноту. Поскольку проектируется средство поддержки принятия решений, то участие ЛПР необходимо:
При использовании различных критериев для оценки значимости двух выборок появляется возможность производить оценку достоверности гипотезы о наличии сдвига и его направлении в выборочных данных о длинах очередей и функции потерь в условиях потока вредоносных заявок. Можно использовать критерий знаков, в силу простоты и эффективности реализующийся различными программными способами. Для выборок одинаковой или дополненной длины можно использовать критерий Кохрена об однородности выборок. Известна [7] формула Поллачека-Хинчина для вычисления среднего числа заявок в системе M/G/1:
По этой формуле можно получить оценки других важнейших системных характеристик узла:
Если производительность обработки задается интервальным выражением μ = μmin, μΔ, …, μmax, то
Имея точные сведения об интенсивности полезных заявок λΠ и предполагая, что интенсивность вредоносных заявок не превосходит λB, получается λ = λΠ + λB. Тогда, используя тождественные преобразования, можно получить систему правил. Входные данные: λΠ, λB, μmin, μmax. Правила расчета:
Поскольку имеется информация о среднем числе заявок от менеджера очередей, то можно построить таблицу значений функции Lq в зависимости от фактических аргументов λ и a = μmax – μmin при μmin = const. Результаты вычислительных экспериментов сводятся в таблицу 3. Таблица 3. Статистические оценки потерь
При использовании алгоритмов стохастической аппроксимации необходимо осуществлять:
В большинстве современных средств мониторинга доступны сведения о текущей длине очереди к узлу и числе заявок в нем, и не всегда доступны другие описательные характеристики. Поэтому требуется определить функцию штрафа, зависящую от числа заявок в модели СМО узла на n-м шаге исполнения алгоритма: ξn = ξL(Ls(n)). Устанавливается величина центрирования Далее рассматриваются следующие варианты выбора стратегий управления совокупностью узлов РС. Поскольку речь идет о РС, то наиболее доступными для изменения ЛПР, таким как системный администратор, является способ коммутации узлов. В специальной литературе [8, 9] известны следующие основные типы топологий: общая шина, звезда, кольцо, дерево, ячеистая. Им соответствуют стратегии коммутации для моделирования: S1 = «общая шина»; S2 = «звезда»; S3 = «кольцо»; S4 = «дерево»; S5 = «ячеистая». И, очевидно, что N=5. Пусть известны Для некоторых алгоритмов статистические оценки функции потерь сведены в таблицу 3. Алг_1 – алгоритм Нарендры-Шапиро, алг_2 – алгоритм Льюса, алг_3 – алгоритм Варшавского-Воронцовой, алг_4 – алгоритм Буша-Мостеллера, алг_5– алгоритм Назина-Позняка. Сценарные модули для расчета характеристик узлов и обеспечения взаимодействия ЛПР с программным комплексом разрабатываются на ЯПВУ Python. С помощью этих модулей обеспечивается принятие решений о необходимости изменения производительности узлов. Вывод В работе описаны программные реализации на ЯПВУ Java ряда алгоритмов стохастической аппроксимации, что позволит использовать актуальные средства и языки разработки. Перспективой дальнейших публикаций станет детальное описание программной реализации СППР на их основе.
Ключевые слова: стохастическая оптимизация. Practical implementation and application of stochastic approximation algorithms Tkachenko K.S., 1st cat. Engineer, Graduate student, Federal State Budget Educational Institution of Higher Education «Sevastopol State University», Sevastopol, Russian Federation, tkachenkokirillstanislavovich@gmail.com Summary: There are the implementations of stochastic optimization algorithms on the high-level programming language Java in this article. Keywords: stochastic optimization. |
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 ТКАЧЕНКО К.С., инженер 1-й кат., аспирант, ФГАОУ ВО «Севастопольский государственный университет», Российская Федерация,
ТКАЧЕНКО К.С., инженер 1-й кат., аспирант, ФГАОУ ВО «Севастопольский государственный университет», Российская Федерация, 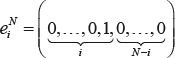
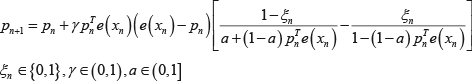 (2)
(2)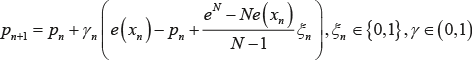 (4)
(4)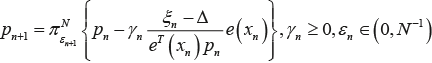 (5)
(5)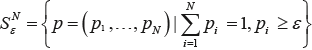
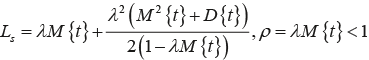 (7)
(7)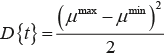 .
.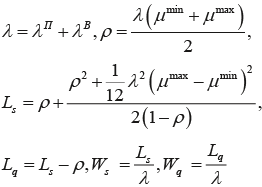 (6)
(6)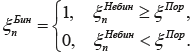 (7)
(7)


