 |
|
|
|
Классическая задача о построении расписания обслуживания для двух устройств
Классическая задача о построении Рассматриваются алгоритм и программные реализации решения задачи Джонсона для двух обслуживающих устройств Современное общество требовательно к отзывчивости, быстродействию, производительности вычислительной техники. Для этого необходимо рационально использовать имеющиеся аппаратно-программные средства, вследствие чего возникает много задач управления ресурсами. Их можно решить различными способами планирования. Планирование организуется, в том числе, комбинаторными методами, разнообразными способами упорядочивания и перебора. Этотрудоемкие, громоздкие задачи, решение которых затруднено или невозможно при неопределенности входных данных. Если же имеется полная определенность о структуре решаемой задачи планирования и входных данных дляупорядочивания, то часто можно использовать методы и средства классической теории расписаний. Существуют алгоритмы для решения задач построения расписаний выполнения заявок для одного процессора, нескольких параллельных ипоследовательных процессоров и многие другие. Выделяются алгоритмы, решение задач с помощью которых представляется в виде вектора. Одной из известнейших и наиболее простых задач теории расписаний является так называемая задача Джонсона с двумя станками. Задача в приложении к информационным технологиям ставится следующим образом. Имеется вычислительная система, состоящая из двух вычислительных процессоров. Заявка последовательно должна быть обслужена вначале на первом процессоре, затем на втором. Пусть число заявок есть n. Тогда для заявок с номерами i= 1, n известны ai – время обслуживания заявки на первом процессоре, bi – время обслуживания заявки на втором процессоре. Один вычислительный процессор единовременно может обслуживать (обрабатывать) только одну заявку. Необходимо составить такое расписание последовательности обработки заявок, при котором суммарное время обработки всех заявок минимально. В наглядном виде на рис. 1 изображена схема двухпроцессорной системы. На рисунке исходная заявка с номером i характеризуется двумя параметрами – ai и bi. Первый вычислительный процессор – I, второй – II.
Рисунок 1. Схема двухпроцессорной системы В классическом виде алгоритм Джонсона достаточно нагляден и удобен для ручного счета [1, §59]. При таком счете заявки упорядочиваются таким образом, чтобы минимальное из времен обработки заявки на I процессоре и следующей заней заявки на II процессоре не превосходило минимального из времен обработки рассматриваемой заявки на II процессоре и следующей за ней заявки на I процессоре. Такая последовательность обработки уменьшает время простоя системы из двух последовательно соединенных процессоров. Другими словами, находится заявка с наименьшим значением либо ai, либо bi. Если найденная величина ai, то заявка записывается в начало расписания, иначе – в конец. После чего заявка исключается из рассмотрения и границы результирующего расписания уплотняются. Но для компьютерных вычислений проще для реализации в парадигме процедурного программирования метод на основе [2, гл. 5, п. 1.2] алгоритма построения оптимального по быстродействию расписания обслуживания заявок. Его можно сформулировать следующим образом:
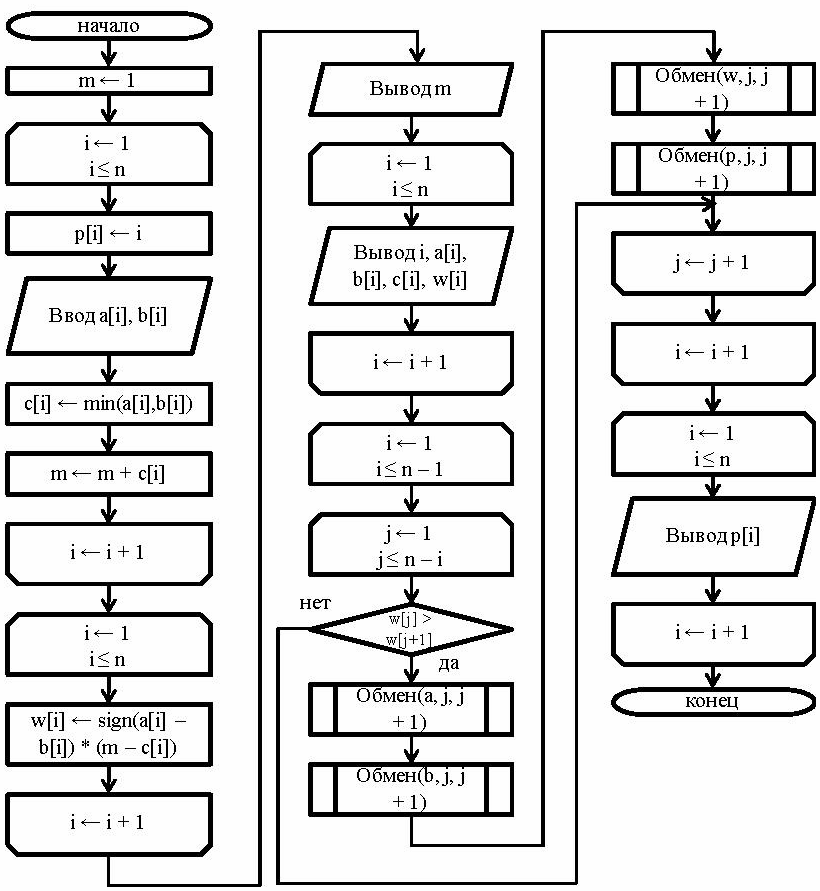
В предположении, что используется алгоритм сортировки пузырьком (для упрощения иллюстрации) и значение M есть m – увеличенная на единицу сумма всех наименьших значений из времен обработки для заявки, псевдокод можно записать следующим образом: 1. Определение массивов целого типа a[1..n], b[1..n], c[1..n], w[1..n], p[1..n]. Определение целочисленных переменных i, j, m = 1. В элементах массивов a[i] и b[i] будут располагаться величины длительности выполнения заявки с номером i. Вэлементе массива c[i] – минимальное из времен выполнения на процессоре a[i] и b[i] для заявки с номером i. В w[i] – рассчитанный относительный вес i-й заявки. p[i] соответствует номеру заявки i и используется для получения итогового расписания. Индексы i и j используются в организации циклов с параметром. Значение целочисленной переменной m заведомо больше любой из величин min(a[i], b[i]) для всех i. 2. Организуется ввод исходных данных, заполнение p[i] и расчет c[i], w[i] для всех заявок. В цикле с параметром для i от 1 до n выполняется: 2.1. Сохраненный номер заявки равен номеру заявки: p[i] ← i. 2.2. Организуется ввод a[i], b[i], в простейшем случае, со стандартного устройства ввода. 2.3. Находится наименьшая из длительностей обработки на вычислительном процессоре: с[i] ← min(a[i], b[i]). 2.4. Накапливается m ← m + c[i]. 3. Формируются веса заявок. При этом для i от 1 до n. 3.1. Рассчитывается вес i-й заявки: w[i] ← sign(a[i] – b[i]) * (M – c[i]). 4. Выполняется вариант сортировки пузырьком. Для i от 1 до n – 1. 4.1. Для j от 1 до n – i. 4.1.1. Если w[j] > w[j + 1]. 4.1.1.1. Обмен(a, j, j + 1). 4.1.1.2. Обмен(b, j, j + 1). 4.1.1.3. Обмен(w, j, j + 1). 4.1.1.4. Обмен(p, j, j + 1). (Значения c[i] безразличны и на этапе сортировки и далее не используются.) 5. Выводится расписание обработки заявок. Для i от 1 до n. 5.1. Вывод порядкового номера заявки в первоначальном списке p[i]. В результате работы алгоритма будет получена последовательность номеров заявок, при которой заявки будут обработаны за минимальное время. Схема алгоритма приводится на рис. 2.
Рисунок 2. Схема алгоритма работы программы Исходные тексты программ приводятся в листинге 1 – на школьном алгоритмическом языке, 2 – Паскале, 3 – Си, 4 – Python. При разработке всех предлагаемых программ была сделана попытка написать такой программный код наразличных языках, который будет максимально близок между разными языковыми реализациями. Поэтому результирующие программы не лаконичны, не всегда эффективны и оптимальны по потребляемым ресурсам. Листинг 1. Исходный текст программы на школьном алгоритмическом языке цел n = 6 алг джонсон нач цел таб a[1:n], b[1:n], c[1:n], w[1:n], p[1:n] цел i, j, m m := 1 нц для i от 1 до n p[i] := i вывод 'a[', i, '] b[', i, '] : ' ввод a[i], b[i] c[i] := мин(a[i], b[i]) m := m + c[i] кц нц для i от 1 до n w[i] := знак(a[i] - b[i]) * (m - c[i]) кц вывод 'M = ', m, нс вывод ' i a b c w', нс нц для i от 1 до n вывод i:4, a[i]:4, b[i]:4, c[i]:4, w[i]:4, нс кц нц для i от 1 до n нц для j от 1 до n - i если w[j] > w[j + 1] то обмен(a, j, j + 1) обмен(b, j, j + 1) обмен(w, j, j + 1) обмен(p, j, j + 1) все кц кц нц для i от 1 до n вывод ' ', p[i] кц вывод нс кон алг цел мин(цел a, цел b) нач если a <= b то знач := a иначе знач := b все кон алг цел знак(цел a) нач если a > 0 то знач := 1 иначе если a = 0 то знач := 0 иначе знач := -1 все все кон алг обмен(аргрез цел таб a[1:n], арг цел i, цел j) нач цел t t := a[i] a[i] := a[j] a[j] := t кон
Листинг 2. Исходный текст программы на языке Паскаль program johnson; const n = 6; type mas = array [1..n] of integer; function min(a, b: integer): integer; begin if a <= b then min := a else min := b; end; function sign(a: integer): integer; begin if a > 0 then sign := 1 else if a = 0 then sign := 0 else sign := -1; end; procedure swap(var a: mas; i, j: integer); var t: integer; begin t := a[i]; a[i] := a[j]; a[j] := t; end; procedure main; var a, b, c, w, p: mas; i, j, m: integer; begin m := 1; for i := 1 to n do begin p[i] := i; write('a[', i, '] b[', i, '] : '); readln(a[i], b[i]); c[i] := min(a[i], b[i]); m := m + c[i]; end; for i := 1 to n do w[i] := sign(a[i] - b[i]) * (m - c[i]); writeln('M = ', m); writeln(' i a b c w'); for i := 1 to n do writeln(i:4, a[i]:4, b[i]:4, c[i]:4, w[i]:4); for i := 1 to n - 1 do for j := 1 to n - i do if w[j] > w[j + 1] then begin swap(a, j, j + 1); swap(b, j, j + 1); swap(w, j, j + 1); swap(p, j, j + 1); end; for i := 1 to n do write(' ', p[i]); writeln; end; begin main; end.
Листинг 3. Исходный текст программы на языке Си #include <stdio.h> #define n 6 int min(int a, int b) { if (a <= b) return a; else return b; } int sign(int a) { if (a > 0) return 1; else if (a == 0) return 0; else return -1; } void swap(int a[], int i, int j) { int t = a[i]; a[i] = a[j]; a[j] = t; } int main(int argc, char * argv[]) { int a[n], b[n], c[n], w[n], p[n]; int i, j, m = 1; for (i = 0; i < n; ++i) { p[i] = i + 1; printf("a[%d] b[%d] : ", i + 1, i + 1); scanf("%d%d", &a[i], &b[i]); c[i] = min(a[i], b[i]); m = m + c[i]; } for (i = 0; i < n; ++i) w[i] = sign(a[i] - b[i]) * (m - c[i]); printf("M = %d\n", m); printf(" i a b c w\n"); for (i = 0; i < n; ++i) printf("%4d%4d%4d%4d%4d\n", i + 1, a[i], b[i], c[i], w[i]); for (i = 0; i < n; ++i) for (j = 0; j < n - i - 1; ++j) if (w[j] > w[j + 1]) { swap(a, j, j + 1); swap(b, j, j + 1); swap(w, j, j + 1); swap(p, j, j + 1); } for (i = 0; i < n; ++i) printf(" %d", p[i]); printf("\n"); return 0; }
Листинг 4. Исходный текст программы на языке Python # -*- coding: utf-8 -*- n = 6 def sign(a): if a > 0: return 1 elif a == 0: return 0 else: return -1 def swap(a, i, j): t = a[i] a[i] = a[j] a[j] = t a = list(range(n)) b = list(range(n)) c = list(range(n)) w = list(range(n)) p = list(range(n)) m = 1 for i in range(n): p[i] = i + 1 s = input('a[%d] b[%d] : ' % (i + 1, i + 1)).strip().split() a[i], b[i] = int(s[0]), int(s[1]) c[i] = min(a[i], b[i]) m = m + c[i] for i in range(n): w[i] = sign(a[i] - b[i]) * (m - c[i]); print('M = %d' % m) print(' i a b c w'); for i in range(n): print('%4d%4d%4d%4d%4d' % (i + 1, a[i], b[i], c[i], w[i])) for i in range(n): for j in range(n - i - 1): if w[j] > w[j + 1]: swap(a, j, j + 1) swap(b, j, j + 1) swap(w, j, j + 1) swap(p, j, j + 1) for i in range(n): print(' %d' % p[i], end='') print() Результаты работы программы (для любого языка) приводятся в листинге 5. Длительности выполнения заданий на процессорах получены с использованием доступного генератора псевдослучайной последовательности. Листинг 5. Результаты работы программы a[1] b[1] : 7 4 a[2] b[2] : 8 3 a[3] b[3] : 9 6 a[4] b[4] : 2 5 a[5] b[5] : 1 10 a[6] b[6] : 5 2 M = 19 i a b c w 1 7 4 4 15 2 8 3 3 16 3 9 6 6 13 4 2 5 2 -17 5 1 10 1 -18 6 5 2 2 17 5 4 3 1 2 6 Итак, в статье мы рассмотрели один из простейших и наиболее известных алгоритмов теории расписаний. Приведена реализация на нескольких языках программирования высокого уровня.
|
КИРИЛЛ ТКАЧЕНКО, инженер 1-й кат., ассистент, аспирант, Федеральное государственное автономное образовательное учреждение высшего образования «Севастопольский государственный университет», 
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
