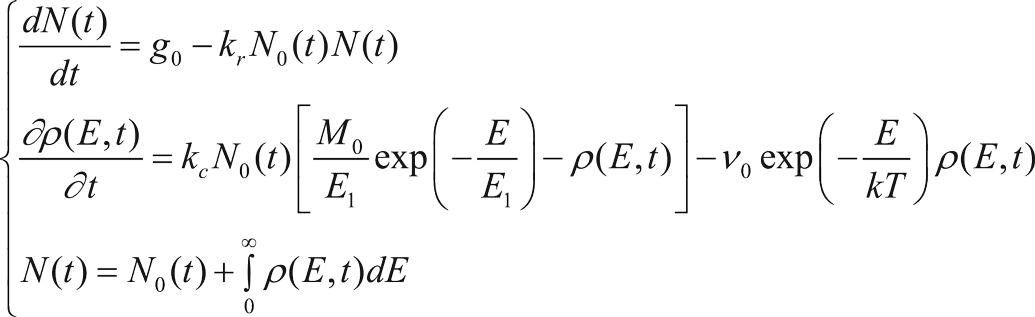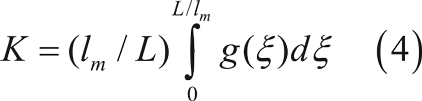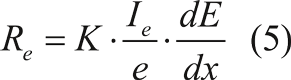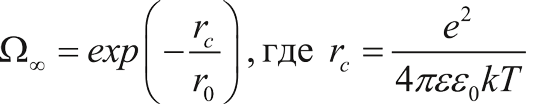Утилиты в ПО MathCAD для уточненного расчета электрических полей при облучении полимерных пленок электронами низких энергий

 ЗВЕЗДОВ Д.С., Национальный исследовательский университет «Высшая школа экономики», dzvezdov@hse.ru

 АБРАМЕШИН Д.А., Национальный исследовательский университет «Высшая школа экономики», dabrameshin@hse.ru

 ГРАНОВСКИЙ В.С., Национальный исследовательский университет «Высшая школа экономики», manianell@mail.ru

Утилиты в ПО MathCAD
для уточненного расчета электрических полей при облучении полимерных пленок электронами низких энергий

В данной работе рассмотрена математическая модель Роуза-Фаулера-Вайcберга, которая анализирует радиационную электропроводность полимерных пленок при облучении электронами низких энергий. В ходе проведенных исследований было разработано специальное программное обеспечение в математической среде MathCAD, которое позволяет проводить расчеты по поглощенной дозе, полевой зависимости и частотному фактору радиационной электропроводности. Данное программное обеспечение используется для проведения экспериментов в лаборатории функциональной безопасности космических аппаратов и систем

Введение

Полимерные материалы нашли широкое применение в различных областях человеческой деятельности, в том числе в космической технике и ядерной энергетике [1]. Как в первом, так и во втором случае при эксплуатации полимерные материалы подвергаются воздействию ионизирующей радиации. Естественно, что при таком воздействии меняются электрофизические свойства этих материалов. Такие изменения свойств принято называть радиационными эффектами. Радиационные эффекты условились делить на два класса: обратимые радиационные эффекты и необратимые эффекты. Необратимые или пострадиационные эффекты имеют место в механических и оптических свойствах полимеров. Например, наблюдается необратимое снижение прочности на разрыв. Основной обратимый радиационный эффект – это эффект значительного увеличения удельной объемной электропроводности полимера в поле действия радиации и быстрого снижения электропроводности при прекращении облучения [2]. Такую электропроводность полимера называют радиационной электропроводностью (РЭ). РЭ – это основной фактор, который контролирует объемное заряжение полимеров при их облучении электронами. Изучению этого явления и посвящена настоящая работа.

Для проведения расчетов РЭ в настоящее время используется полуэмпирическая модель Роуза-Фаулера-Вайсберга (РВФ) [3]:

В данной системе уравнений (1) приняты следующие обозначения:

• N(t) – полная концентрация основных носителей заряда (в дальнейшем электронов);
• g₀ – скорость объемной генерации носителей заряда;
• k_r – коэффициент объемной рекомбинации подвижных электронов с дырками, выступающими в качестве центров рекомбинации;
• k_c – константа скорости захвата квазисвободных электронов на ловушки;
• M₀ – суммарная концентрация ловушек, экспоненциально распределенных по энергии (E > 0 и отсчитывается вниз от дна зоны переноса);
• ρ(E,t) – энергетическая плотность распределения захваченных электронов;
• ν₀ – эффективный частотный фактор термического освобождения носителей заряда из ловушек;
• E₁ – параметр экспоненциального распределения ловушек по энергии.

Как видно из системы уравнений модели РФВ, концентрация носителей заряда в проводящем состоянии N₀(t) с микроскопической подвижностью μ₀ вычисляется при решении системы уравнений РФВ.

По определению плотность радиационного тока описывается следующим выражением:

где:

• F – величина приложенного электрического поля [В/м];
• γ_r – радиационная электропроводность [Ом^-1м^-1];;
• e – заряд электрона [Кл].

Заряд электрона и микроскопическая подвижность являются постоянными величинами, следовательно, на кинетику радиационной электропроводности и ее полевую зависимость влияет исключительно кинетика изменения концентрации носителей заряда в проводящем состоянии N₀(t).

Генерация носителей заряда

Концентрация генерируемых носителей заряда определяется мощностью дозы ионизирующей радиации. Для случая электронного излучения имеет место специфическое распределение мощности поглощенной дозы по толщине образца.

Рисунок 1. Кривая распределения поглощенной дозы электронного излучения по глубине образца полимерного материала (полиэтилентерефталата)

Нами экспериментально определено это распределение (см. рис. 1) для электронов с энергией (30...65) кэВ, которое аппроксимировано аналитической функцией:

В выражении (3) ξ – это отношение текущей толщины образца полимера к величине максимального пробега электронов данной энергии в рассматриваемом полимере l_m.

С помощью ПО MathCAD была создана программа расчета поглощенной дозы с учетом фактора ее накопления по глубине образца. Сам фактор накопления поглощенной дозы определятся выражением:

Из рис. 1 мы видим, что глубинный ход дозы по образцу является сильно неравномерным. Кривая проходит через максимум и затем спадает до нуля в конце пробега электронов. Рост поглощенной дозы с глубиной на начальном участке кривой объясняется тем, что сечение взаимодействия, плотность ионизации и, соответственно, поглощенная доза растут по мере того, как электрон теряет свою энергию в соударениях с молекулами среды. Однако общее количество первичных электронов, проходящих через слои образца, с ростом глубины падает, что приводит к уменьшению поглощенной дозы с увеличением глубины. Это хорошо видно на конечном участке кривой. Конкуренцией вышеуказанных факторов иобъясняется наличие максимума на кривой глубинного хода дозы.

Для точного расчета поглощенной дозы электронного излучения при использовании даже тонких образцов, толщина которых соизмерима с величиной пробега электронов в данном образце, необходимо учитывать пространственную зависимость мощности поглощенной дозы. Мощность дозы электронного излучения определяется при этом как:

где

• R_e – расчетная (усредненная) мощность дозы электронного излучения;
• K – фактор накопления поглощенной дозы из выражения (4);
• I_e – плотность тока облучающих образец электронов;
• dE/dx – тормозная способность полимерного материала для электронов данной энергии (значение выбирается из таблиц), определяющая мощность дозы на облучаемой поверхности.

Входными данными для расчета мощности поглощенной дозы являются плотность тока облучающих образец электронов, энергия электронов, толщина образца и тип полимерного материала, из которого приготовлен образец.

Полевая зависимость

Полевая зависимость РЭ полимеров обусловлена влиянием приложенного электрического поля на радиационно-химический выход зарядов, принимающих участие в переносе электрического тока. Вероятность Ω_∞ того, что электронно-дырочная пара будет разделена, определяется начальным расстоянием разделения зарядов в ней, типичное значение которого составляет r₀ = 6 нм.

Вероятность разделения пары электрон – материнский ион является нелинейной функцией приложенного электрического поля. Это приводит к тому, что при увеличении поля в два раза электропроводность может возрасти в три, в четыре раза. Причем такое поведение РЭ характерно для сильных полей. В слабых полях зависимость РЭ от приложенного поля независит.

Примем следующие обозначения:

• ε₀ – электрическая постоянная, [Ф/м];
• ε – относительная диэлектрическая проницаемость среды;
• k – постоянная Больцмана, [Дж/К];
• e – заряд электрона, [Кл];
• T – температура, 290 [К].

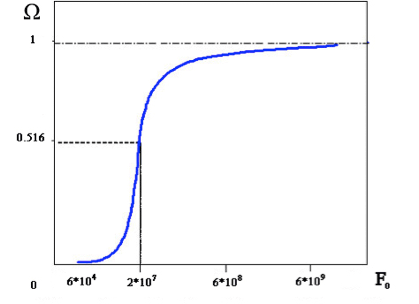
Вероятность разделения в отсутствие внешнего электрического поля равна:

так называемый радиус Онзагера, определяющий сферу кулоновского взаимодействия зарядов геминальной пары при температуре T среды.

В области средних и сильных электрических полей используется предложенная Онзагером формула:

Для расчета полевой зависимости радиационной электропроводности полимера была разработана подпрограмма MathCAD. Результаты вычислений программы для случая средних исильных полей наглядно представлены на следующем графике (см. рис. 2).

Рисунок 2. Кривая зависимости вероятности разделения электронно-дырочной пары от приложенного поля

Захват и высвобождение электронов с ловушек

Итак, как было указано выше, ионизирующее излучение воздействует на непроводящий в обычном состоянии материал, выбивая из атомов этого материала электроны. Таким образом, образуются дырки, которые принимаются неподвижными, и электроны, свободно дрейфующие по объему материала.

Необходимо учитывать, что движение электрона происходит среди дырок (ионов) и ловушек, энергия которых распределена по экспоненциальному закону. Определение характеристики рекомбинации – процесса захвата ионизированным атомом движущегося электрона – необходимо для вычисления величины радиационной электропроводности материала. Не менее важную роль играет частотный фактор – частота попыток выхода электрона с ловушки. С его ростом максимальная электропроводность увеличивается, а время установления квазиравновесия, наоборот, сокращается.

Можно заключить, что процесс переноса тока в объеме полимера происходит посредством многочисленных последовательных серий захватов электронов на ловушки ипоследующих освобождений с них. Поэтому модель РФВ также известна как модель многократного захвата.

Процессы многократного захвата описывают два последних уравнения модели РФВ. Необходимо иметь в виду, что процесс прямого обмена электронами между ловушками нерассматривается. Перераспределение электронов по ловушкам происходит исключительно посредством зоны проводимости, в которую забрасываются электроны за счет теплового движения.

Заключение

В настоящей работе рассмотрена полуэмпирическая модель РЭ Роуза-Фаулера-Вайсберга. При анализе данной модели установлено, что ее необходимо дополнить сторонним программным обеспечением для проведения расчетов объемного заряжения полимеров электронами. Это стороннее программное обеспечение должно учитывать три аспекта, которые отсутствуют в модели РФВ. Во-первых, это уточненный расчет генерации носителей заряда, который учитывает реальное распределение поглощенной дозы по глубине образца. Во-вторых, расчет электрических полей в полимере при их облучении электронами должен принимать во внимание сверхлинейную зависимость радиационного тока отэлектрического поля, которая в разработанной подпрограмме MathCAD дается в виде решения задачи Онзагера в области средних и сильных полей. Здесь следует отметить, чтоуказанная сверхлинейность вольт-амперной характеристики радиационного тока способствует снижению максимально достижимого электрического поля в полимере при егооблучении электронами. И, наконец, третья уточняющая процедура – это рост РЭ за счет сверхлинейной зависимости частотного фактора ν0, присутствующего в модели РВФ (1), отэлектрического поля за счет эффекта Пула-Френкеля.

Предложенные утилиты предназначены в первую очередь для того, чтобы создать более комфортные условия при проведении экспериментальных испытаний в Учебно-исследовательской лаборатории Функциональной безопасности космических аппаратов и систем МИЭМ НИУ ВШЭ. Кроме того, эти утилиты планируется встроить в программу расчета электрических полей, возникающих при облучении полимеров электронами, для проведения более корректных расчетов этих полей. eof

1. Тютнев А.П., Саенко В.С., Пожидаев Е.Д., Костюков Н.С. Диэлектрические свойства полимеров в полях ионизирующих излучений. – М.: «Наука», 2005. – 453 с.
2. Тютнев А.П., Ихсанов Р.Ш., Саенко В.С., Пожидаев Е.Д. Теоретический анализ модели Роуза-Фаулера-Вайсберга //. Высокомолек. соед. А. 2006. Т. 48. №11. – С. 2015-2022.
3. Безродных И.П., Тютнев А.П., Семенов В.Т. Радиационные эффекты в космосе / Отв. ред.: А. П. Тютнев. Ч. 2: Воздействие космической радиации на электротехнические материалы. – М.: АО «Корпорация «ВНИИЭМ», 2016.

Ключевые слова: радиационная физика; программное обеспечение, MathCAD, полимерные материалы, полевая зависимость, частотный фактор, мощность поглощенной дозы.

The MathCAD based mathematical packet for calculating electric fields in polymer films irradiated with low energy electrons

D. S. Zvezdov, , D. A. Abrameshin, V. S. Granovsky

National Research University Higher School of Economics

Summary: The Rose-Fowler-Vaisberg model which analyzes polymer radiation conductivity at strong electric fields has been considered. Special software has been developed based on the MathCAD mathematical packet. We employed it to calculate the absorbed dose, the field dependent conductivity and the frequency factor of the model as well as to analyze experimental data obtained in the Laboratory of Space Vehicles and Systems Functional Safety.

Keywords: Radiation physics, software, MathCAD, polymers, field dependency, absorbed dose, frequency factor.

Комментарии могут оставлять только зарегистрированные пользователи