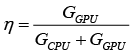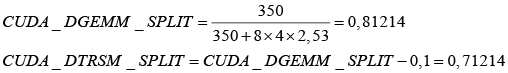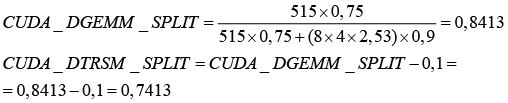Исследование воздействия некоторых параметров теста LINPACK для гибридного кластера на производительность вычислений в зависимости от размерности задачи

 КУЛИКОВ В.А., аспирант кафедры прикладной математики, информатики и вычислительной техники факультета электроники и системотехники Московского государственного университета леса, Vladimir.Kulikov@rsce.ru

 ЧЕРНЫШОВ А.В., к.т.н., доцент кафедры прикладной математики, информатики и вычислительной техники факультета электроники и системотехники Московского государственного университета леса, sch@mgul.ac.ru

Исследование воздействия некоторых параметров теста LINPACK
для гибридного кластера на производительность вычислений в зависимости от размерности задачи

При решении систем линейных алгебраических уравнений на современных гибридных (CPU + GPU) кластерах перед пользователем возникает задача выбора значений ряда параметров, оказывающих существенное, но неочевидное влияние на производительность вычислений и, как следствие, на временные, а следовательно, и технические затраты на решение задачи. Существующие рекомендации по выбору значений этих параметров носят оценочный характер и не гарантируют достижения максимальной производительности вычислений при заданной размерности системы линейных алгебраических уравнений. Целью работы является экспериментальное исследование влияния значений параметров Nb и CUDA_DGEMM_SPLIT теста LINPACK, представляющего собой решение модельной системы линейных алгебраических уравнений методом LU-разложения, на производительность вычислений на гибридных узлах кластера «Ломоносов» (МГУ, Москва). Получены рекомендательные данные значений параметров Nb и CUDA_DGEMM_SPLIT в зависимости от размерности системы линейных алгебраических уравнений для достижения максимальной производительности при решении системы линейных алгебраических уравнений методом LU-разложения на гибридных вычислительных узлах кластера «Ломоносов». Построенная в работе рекомендательная таблица для кластера «Ломоносов» позволяет однозначно выбирать значения параметров Nb и CUDA_DGEMM_SPLIT в зависимости от размерности системы линейных алгебраических уравнений для достижения максимальной производительности вычислений

Введение

Параллельные вычисления – современная, бурно развивающаяся область вычислительной науки. Актуальность данной области складывается из множества факторов, и в первую очередь из потребности в больших вычислительных ресурсах для решения расчетных задач в различных областях науки и техники.

Например, при создании перспективных образцов авиационной и космической техники возникает необходимость в моделировании сложных процессов внешнего обтекания твердых тел различной формы и течения в сложных каналах, вычисления поля давлений и температур потока, расчета коэффициентов сопротивления и потерь полного давления в широком диапазоне скоростей – «дозвук», «трансзвук», «сверхзвук» и «гиперзвук». Для достижения наилучших возможностей по параллельному режиму счета и по количеству внедренных вкод математических моделей физических явлений при обработке наиболее ресурсоемких задач требуется использовать программное обеспечение OpenFOAM.

Практический опыт показывает, что нестационарная задача движения вязкой жидкости в рамках двухпараметрической модели турбулентности на промежутке времени в 10 секунд сиспользованием сеточной модели в 60 млн ячеек на 8 расчетных узлах (2хCPU – Intel Sandy Bridge-EP E5-2665 – 16 расчетных ядер) решается с использованием стандартного решателя OpenFOAM примерно 6 месяцев.

Одно из направлений в повышении эффективности параллельных вычислений – использование параллельных вычислительных кластеров на основе графических процессоров (GPU), что на порядок повышает вычислительные возможности и минимизирует архитектуру и энергопотребление.

Например, компания «Т-Платформы» (производитель кластера «Ломоносов») показала, что более 80% расчетного времени при решении указанной выше задачи занимает решение СЛАУ, и в случае применения гибридного вычислителя (CPU + GPU) удается достигнуть сокращения сроков вычисления до 3 недель.

Одной из важных проблем при решении СЛАУ на гибридном вычислительном кластере является подбор параметров распараллеливания алгоритма вычисления, в частности, распределение количества вычислительной работы между CPU и GPU. В качестве модельной задачи, позволяющей исследовать эту проблему, хорошо подходит стандартный тест LINPACK, широко применяемый для оценки производительности вычислительных кластеров.

В статье [1] были описаны исследования производительности теста LINPACK в версии для гибридных узлов (CPU + GPU) на кластере «Ломоносов» МГУ им. М.В. Ломоносова дляразных размерностей задачи N (от 20 000 до 60 000) и стандартных (рекомендованных) остальных значений параметров теста.

В настоящей статье приведены результаты дальнейших исследований, касающиеся эффективности вычислений теста LINPACK при изменении параметров Nb (величина размерности логических блоков Nb × Nb, на которые разбивается исходная матрица) и CUDA_DGEMM_SPLIT (процент работы, загружаемой в GPU для умножения матриц сдвойной точностью), тесно связанных с аппаратной структурой вычислительных узлов кластера. Причем, как и в статье [1], под эффективностью понимается достижение максимальной производительности вычислений, выражаемое в общепринятых единицах GFlops.

Полученные экспериментальные зависимости могут быть полезны для выбора значений этих параметров при решении реальных систем линейных уравнений конкретных размерностей N с максимальной производительностью.

В статье сознательно не рассматриваются вопросы обусловленности самой математической системы, точности решения, выбора разрядности вычислений, поскольку они должны быть математически обоснованы и решены постановщиком задачи до выхода на вычислитель.

Описание теста

Тест LINPACK представляет собой задачу решения системы линейных алгебраических уравнений (СЛАУ) методом LU-разложения и считается на сегодня классическим способом определения производительности кластера, поскольку к решению СЛАУ сводятся очень многие реальные расчетные задачи.

Тест и его основные параметры, а также характеристики кластерного вычислителя «Ломоносов» подробно рассмотрены в статье [1].

В работе [2] полностью описываются теоретические основы теста LINPACK, а также его возможные варианты для оценки производительности различных компьютерных систем.

Публикация [3] раскрывает имплементацию алгоритма LINPACK для систем высокопроизводительных вычислений.

Основным автором исходного кода LINPACK для GPU (CUDA-enabled version of HPL 2.0 optimized for Tesla 20-series GPU Fermi version 1.5) является доктор Массимилиано Фатика (doctor M. Fatica, NVIDIA).

Основное отличие LINPACK для GPU заключается в том, что в исходном коде HPL 2.0 ядра и CPU, и GPU с небольшими модификациями или без модификаций используются совокупно (эффективность совокупности CPU и GPU превышает сумму их индивидуальных эффективностей):

• Библиотека узла прерывает вызовы кDGEMM иDTRSM ивыполняет иходновременно наядрах CPU иGPU, где:
  • DGEMM – Double-precision General Matrix Multiply – умножение матриц с двойной точностью;
  • DTRSM – Double-precision TRiangular Solve Multiple (solution of the triangular systems of linear equations) – решение треугольных систем линейных уравнений с двойной точностью.
• Использование pinned memory для быстрых передач данных по компьютерной шине PCI Express со скоростью до 5.7 GB/s на слотах x16 gen2.

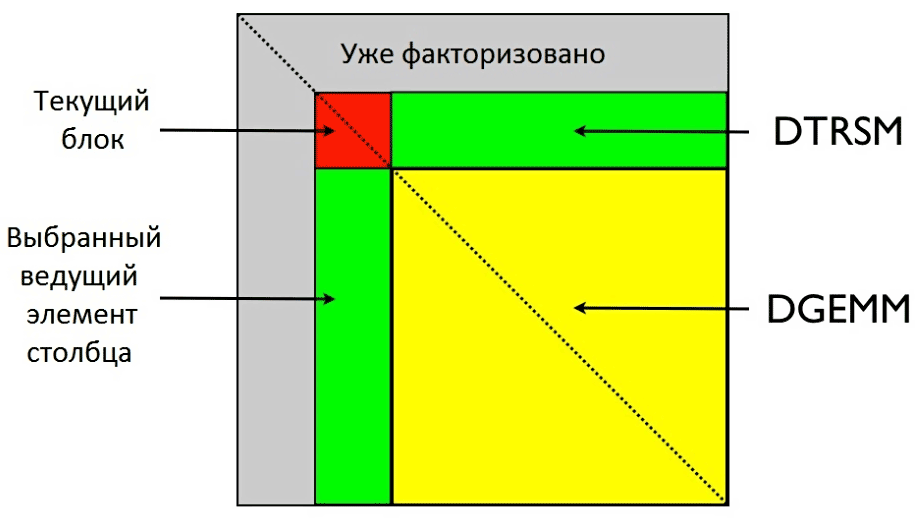
Схема вычислений в LINPACK для GPU показана на рис. 1. Из него видно, что после факторизации текущего блока (красный цвет) обновляются части зеленого и желтого цвета. Чем больше значение размерности N, тем больше времени расходуется на обновление (DGEMM).

• DGEMM – область умножения матриц с двойной точностью;
• DTRSM – область решения треугольных систем линейных уравнений с двойной точностью.

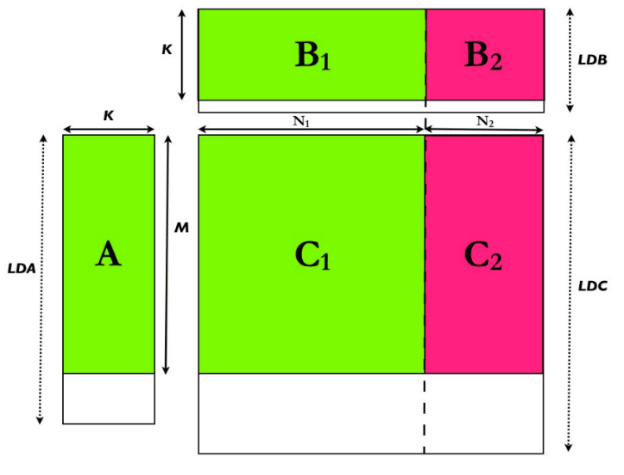
Рисунок 1. Факторизация текущего блока

В версии теста LINPACK для GPU мы опираемся на два преобразования с матрицами – DGEMM и DTRSM. Для их ускорения мы используем все вычислительные возможности CPU и GPU. Эффективное распределение расчетной нагрузки и минимизация времени обмена данными позволят получить наибольшую производительность.

Один из разработанных методов оптимизации для получения наибольшей производительности – оптимальное разделение рабочей нагрузки, которое состоит в следующем.

Если мы имеем матрицы с размерностями A (M , K), B (K , N) и C (M , N) (см. рис. 2), то при выполнении DGEMM-преобразования выполняется 2 × M × K × N операций.

Рисунок 2. Оптимальное разделение рабочей нагрузки

Временно́е равенство вычислений для CPU и GPU:

T_cpu (M, K, N₂) = T_gpu (M, K, N₁)

N = N₁ + N₂

где:

• T_cpu – время вычислений на CPU;
• T_gpu – время вычислений на GPU.

Если для DGEMM-преобразования G_CPU – значение производительности CPU, а G_GPU – значение производительности одного из GPU в размерности GFlops, то оптимальным разделением будет:

Схема метода показана на рис. 2, где:

• зеленым отмечена область GPU, а розовым цветом – CPU;
• A, B, C – матрицы;
• M – величина, определяющая число строк матрицы op(A) и матрицы C;
• N₁ – величина, определяющая число столбцов матрицы op(B₁) и число столбцов матрицы C₁ в области GPU;
• N₂ – величина, определяющая число столбцов матрицы op(B₂) и число столбцов матрицы C₂ в области CPU;
• K – величина, определяющая число столбцов матрицы op(A) и число строк матрицы op(B).

Остановимся на преобразовании DGEMM [4], которое представляет собой следующую процедуру мультипликации матриц:

C := α×op(A)×op(B) + β×C

где op(X) принимает одно из следующих значений:

op(X) = X или op(X) = X^T

Здесь:

• α, β – скалярные величины;
• A, B, C – матрицы;
• op(A) – матрица с числом строк m и столбцов k;
• op(B) – матрица с числом строк k и столбцов n;
• C – матрица с числом строк m и стобцов n;
• X^T – транспонированная матрица X.

Преобразование DGEMM оформлено в виде функции:

DGEMM = (TRANSA, TRANSA, M, N, K, ALPHA, A, LDA, B, LDB, BETA, C, LDC)

Здесь:

• TRANSA – переменная символьного типа, на входе ее значение определяет формат матрицы op(A), который будет использоваться в мультипликации матриц:

TRANSA = 'N'||'n' , op(A) = A

TRANSA = 'T'||'t' , op(A) = A^T

TRANSA = 'C'||'c' , op(A) = A^T

Не изменяется на выходе;

• TRANSB – переменная символьного типа, на входе ее значение определяет формат матрицы op(B), который будет использоваться в мультипликации матриц:

TRANSB = 'N'||'n' , op(B) = B

TRANSB = 'T'||'t' , op(B) = B^T

TRANSB = 'C'||'c' , op(B) = B^T

Не изменяется на выходе;

• M – переменная целого типа, на входе ее значение определяет число строк матрицы op(A) и число строк матрицы C, не изменяется на выходе;
• N – переменная целого типа, на входе ее значение определяет число столбцов матрицы op(B) и число столбцов матрицы C, не изменяется на выходе;
• K – переменная целого типа, на входе ее значение определяет число столбцов матрицы op(A) и число строк матрицы op(B), не изменяется на выходе;
• ALPHA – переменная двойной точности, на входе ее значение определяет скалярную величину α, не изменяется на выходе;
• A – массив двойной точности с размерностью (LDA, ka), где ka – это k, когда TRANSA = 'N'||'n' или, во всех других случаях, m. Перед вхождением с TRANSA = 'N'||'n', ведущая часть массива A размером m на k должна содержать матрицу A, иначе ведущая часть массива A размером k на m должна содержать матрицу A. Не изменяется на выходе;
• LDA – переменная целого типа, на входе определяет первичную размерность матрицы A, когда TRANSA = 'N'||'n', то LDA должно быть не меньше max(1,m), иначе LDA должно быть не меньше max(1,k). Не изменяется на выходе;
• B – массив двойной точности с размерностью (LDB, kb), где kb – это n, когда TRANSB = 'N'||'n' или, во всех других случаях, k. Перед вхождением с TRANSB = 'N'||'n', ведущая часть массива B размером k на n должна содержать матрицу B, иначе ведущая часть массива B размером n на k должна содержать матрицу B. Не изменяется на выходе;
• LDB – переменная целого типа, определяет первичную размерность матрицы B, когда TRANSB = 'N'||'n', то LDB должно быть не меньше max(1,k), иначе LDB должно быть неменьше max(1,n). Не изменяется на выходе;
• BETA – переменная двойной точности, на входе ее значение определяет скалярную величину β, когда значение BETA ноль, то для C не определяются входные данные. Неизменяется на выходе;
• C – массив двойной точности с размерностью (LDC, n). До входа ведущая часть массива С размером m на n должна содержать матрицу C, кроме случая, когда значение β ноль и для этого случая для C не определяются входные данные. На выходе массив C перезаписывается m на n матрицей (α×op(A)×op(B) + β×C);
• LDC – переменная целого типа, на входе определяет первичную размерность матрицы C; LDC – должна быть не меньше max(1,m). Не изменяется на выходе.

В отличие от классического теста LINPACK в его «кластерном» варианте требуется подбор параметра Nb и ряда других параметров в целях достижения максимальной производительности [5]. В частности, представляет интерес подбор значения параметра CUDA_DGEMM_SPLIT (процент работы, загружаемой в GPU для умножения матриц сдвойной точностью).

Описываемый эксперимент сводился к выполнению теста LINPACK на выделенных узлах кластера «Ломоносов» для сетки исходных значений, задаваемой параметрами N, Nb, ипри рекомендованных значениях остальных параметров теста.

В частности, значение параметра Nb зависит от характеристик параллельной вычислительной системы в целом и должно подбираться индивидуально для каждой системы. Дляполучения результатов, близких к пиковым, М. Фатика [6] рекомендует использовать значение Nb = 768 для гибридных кластеров CPU + GPU. Также он указывает, что иногда большую производительность можно достигнуть при Nb = 1024: «…768 typically gives best results, larger values may give better results (1024) if several GPUs share the same PCIe connection…» [7].

Максимально допустимое значение параметра N – размерность задачи, рассчитывается по формуле:

Общая память узлов = Число узлов × Память узла Гб × 1024 ×× 1024 × 1024

В нашем случае:

• Память узла – равняется 24 Гб;
• Коэффициент размера – сколько памяти от Общей памяти узлов необходимо для расчетов теста, чтобы операционная система могла выполнять необходимые операции. Дляконфигурации используемой экспериментальной установки этот коэффициент 0,75;
• Объём памяти для каждого элемента с двойной точностью – равняется 8 байт;
• Вычисленное значение N = 69511,425. Для «укладки» размерности задачи N c использованием Nb = 1024 в начальные условия запуска LINPACK для GPU, с учетом аппаратной конфигурации узлов, чтобы не происходило переполнение памяти при работе программы, принимается значение N = 60000.

Коэффициент CUDA_DGEMM_SPLIT может определяться по различным методикам для запуска теста LINPACK на гибридных узлах кластера CPU + GPU. С ним также тесно связан параметр CUDA_DTRSM_SPLIT (процент работы, загружаемой в GPU для решения треугольных систем линейных уравнений с двойной точностью. Получается вычитанием из CUDA_DGEMM_SPLIT значения 0,1):

1) По эмпирическим значениям, предложенным М. Фатика [6]:

CUDA_DGEMM_SPLIT = 0,836

CUDA_DTRSM_SPLIT = 0,736

2) По методике М. Фатика [7]:

CUDA_DGEMM_SPLIT = 

где:

• MKL_NUM_THREADS – число используемых ядер CPU на одно GPU;
• CPU_FREQ – частота CPU в ГГц.

В нашем случае:

3) По методике расчета Ш. Тарлетон [8]:

где:

• GPU_PEAK_FLOPS – теоретическое пиковое значение производительности GFlops для GPU;
• CPUFLOPS_PER_CLOCK – число операций за 1 такт процессора, позволяющее теоретически достичь пиковой производительности. Для данного типа процессора Intel Xeon L5630 значение CPUFLOPS_PER_CLOCK = 4;
• MKL_NUM_THREADS – число используемых ядер CPU на одно GPU;
• CPU_FREQ – частота CPU в ГГц.

Тогда:

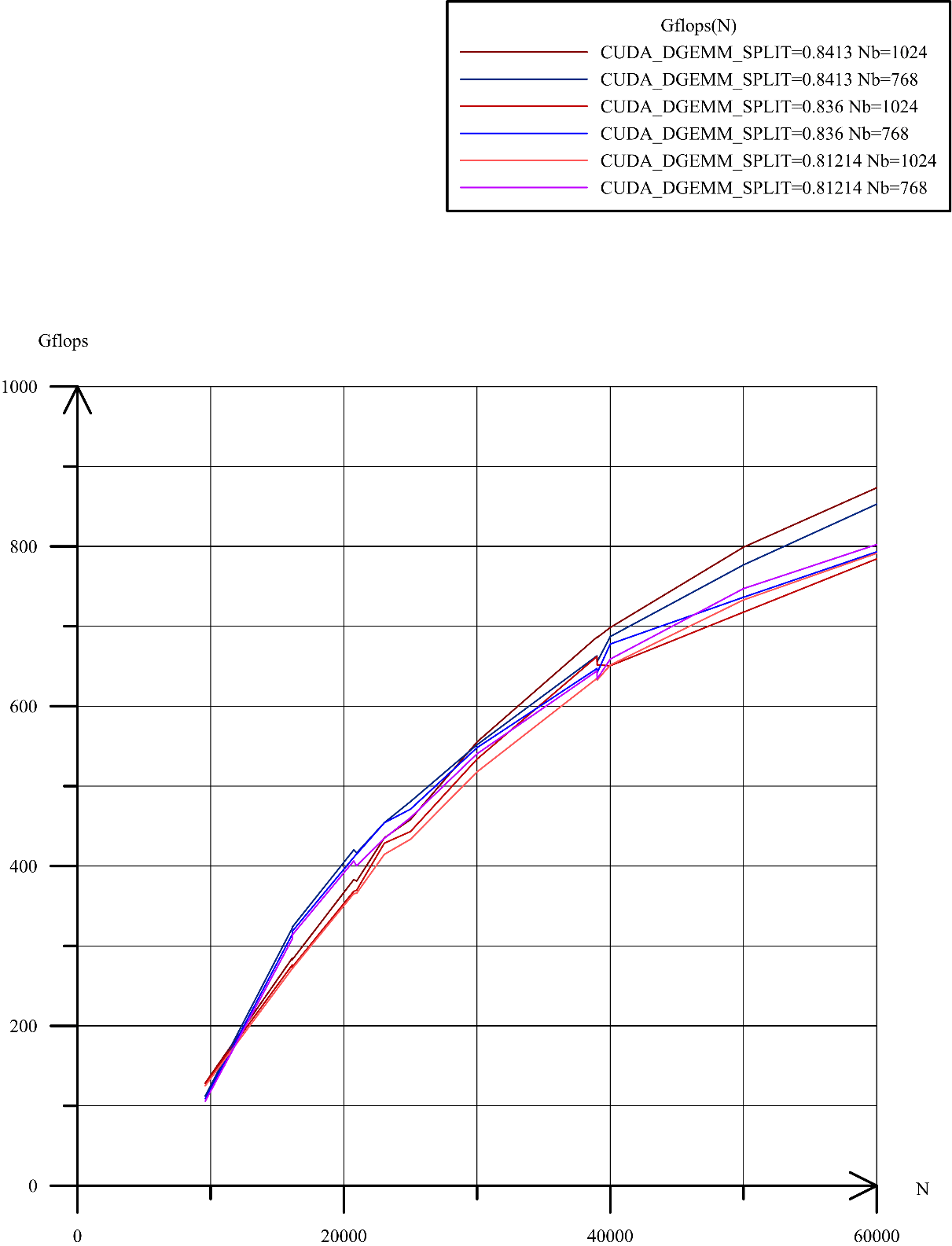
Результаты теста и выводы

Построим графики зависимости производительности кластера GFlops от размерности задачи N для вычисленных CUDA_DGEMM_SPLIT и CUDA_DRSM_SPLIT при Nb = 768 и Nb= 1024 в соответствии с полученными результатами (см. рис. 3).

Рисунок 3. Зависимость производительности вычислений GFlops от размерности задачи N

По графикам на рис.3 можно видеть, что:

• наблюдается картина увеличения производительности для CUDA_DGEMM_SPLIT = 0,8413 при малом значении N с Nb = 1024 в сравнении с другими результатами, получаемыми с CUDA_DGEMM_SPLIT, равными 0,81214 и 0,836;
• для значения CUDA_DGEMM_SPLIT = 0,8413 скорость роста производительности с увеличением N по сравнению с другими значениями CUDA_DGEMM_SPLIT является максимальной.

По верхней огибающей группы построенных графиков была построена рекомендательная таблица (см. таблицу 1) для выбора параметров Nb и CUDA_DGEMM_SPLIT взависимости от размера задачи N для получения максимальной производительности GFlops при решении СЛАУ методом LU-разложения на гибридных узлах кластера «Ломоносов»:

Таблица 1. Рекомендательная таблица

Проведение экспериментов с различными рекомендованными разработчиком значениями размера блока Nb равным 768 и 1024 и вычисленными по разным методикам значениями CUDA_DGEMM_SPLIT, равными 0,81214, 0,8413, 0,836, показало, что максимальной производительности GFlops на гибридных узлах кластера «Ломоносов» удается достичь привыборе значения CUDA_DGEMM_SPLIT = 0,8413, полученного с использованием методики Ш. Тарлетон [8]. При этом значения параметра Nb изменяются в зависимости отразмерности поставленной задачи.

1. Куликов В. А. Исследование возможностей GPU в высокопроизводительных вычислениях. // «В мире научных открытий», №12.2(60), 2014 г. – C. 639-650.
2. J. Dongarra, P. Luszczek, A. Petiet. The LINPACK Benchmark: past, present and future. // Concurrency and Computation: Practice and Experience. 2003. Vol. 15(9). P. 803-820. doi:10.1002/cpe.728.
3. Petitet, R. C. Whaley, J. Dongarra, A. Cleary. HPL Algorithm. Innovate Computer Laboratory (University of Tennessee, Computer Science Department), 2008. – URL:http://www.netlib.org/benchmark/hpl/algorithm.html (дата обращения 20.05.2015).
4. J. Dongarra, I. Duff, J. D. Croz, S. Hammarling. Subroutine DGEMM, 1989. – URL:http://www.netlib.org/lapack/explore-3.2-html/dgemm.f.html (дата обращения 20.05.2015).
5. Petitet, R. C. Whaley, J. Dongarra, A. Cleary. HPL 2.0.Innovate Computer Laboratory (University of Tennessee, Computer Science Department), 2008. – URL:http://www.netlib.org/benchmark/hpl/tuning.html (дата обращения 20.05.2015).
6. E. Phillips, M. Fatica. CUDA-enabled version of HPL 2.0 optimized for Tesla 20 series GPU Fermi version 1.5. Nvidia Corp., 2012. – URL:https://devtalk.nvidia.com/default/topic/500340/cuda-accelerated-LINPACK-code-available (дата обращения 23.05.2015).
7. M. Fatica. Accelerating LINPACK with CUDA on heterogenous clusters. // ACM International Conference Proceeding Series. Vol. 383.
8. S. Tarleton. Power Efficient LINPACK on GPUs, 2012. – URL:http://www.shanetarleton.com/power-efficient-LINPACK-on-gpus (дата обращения 17.06.2015).

Ключевые слова: графический процессор, кластер, высокопроизводительные вычисления, размерность задачи, гибридный вычислительный узел, LINPACK, решение СЛАУ, GFlops.

The research values of certain parameters of the LINPACK benchmark for hybrid cluster effects on the compute performance as a function of the problem sizes

Kulikov V. A., Post-Graduate Student, Department of Applied Mathematics, Computer Science and Computer Engineering Faculty of Electronics and Systems Engineering of the Moscow State Forest University (MSFU), Vladimir.Kulikov@rsce.ru

Chernyshov A. V., PhD, Tech., Associate Professor, Department of Applied Mathematics, Computer Science and Computer Engineering Faculty of Electronics and Systems Engineering of the Moscow State Forest University (MSFU), sch@mgul.ac.ru

Summary: When solving systems of linear algebraic equations with modern, hybrid (CPU GPU) clusters to the user, there arises the problem of selecting values of a number of parameters that have a significant, but unobvious subjection on computing performance and, as a consequence, on time, and, therefore, and technical resources for the solution of the problem. The existing recommendations on the selection of values for these parameters are evaluatives and do not guarantee the best performance computing for a given dimension of the system of linear algebraic equations. The purpose of this work is experimental research of the subjection of the values of the parameters Nb and CUDA_DGEMM_SPLIT LINPACK benchmark, representing a solution of model system of linear algebraic equations by the method of LU decomposition, for the performance computing of hybrid nodes of the cluster «Lomonosov» (Moscow State University, Moscow, Russia Federation). Recommendatory data of the values of the parameters Nb and CUDA_DGEMM_SPLIT LINPACK depending on the dimension of system of linear algebraic equations for achievement of the maximum performance for solving system of linear algebraic equations are obtained by LU decomposition method on hybrid computing nodes of a cluster «Lomonosov». The recommendatory data table constructed in this research work for a cluster «Lomonosov» allows to select unambiguously values of the Nb and CUDA_DGEMM_SPLIT parameters depending on dimension of system of linear algebraic equations for achievement of the maximum computing performance.

Keywords: GPU, cluster, high-performance computing, problem size, hybrid computing node, solving linear systems of equations, GFlops.

Комментарии могут оставлять только зарегистрированные пользователи