Кожевников А.М., д.т.н., профессор, Национальный исследовательский университет «Высшая школа экономики», AKozhevnikov@hse.ru

 Тумковский С.Р., д.т.н., профессор, Национальный исследовательский университет «Высшая школа экономики», STumkovskiy@hse.ru

Математическая макромодель вибрации
этажерочной конструкции радиоэлектронной аппаратуры

В работе рассматривается метод построения макромодели динамики этажерочной конструкции радиоэлектронной аппаратуры в частотной области на основе методов конечных элементов и электромеханической аналогии. Для построения макромодели использован математический аппарат собственных значений. В макромодели реализована аналитическая зависимость выходной характеристики от частоты воздействия. Построенная макромодель имеет размерность, равную количеству варьируемых в процессе оптимизации параметров, что многократно сокращает время, затрачиваемое на оптимизацию при малом количестве варьируемых параметров

Проблема

Современная радиоэлектронная аппаратура (РЭА), особенно бортовая, часто эксплуатируется в условиях внешних механических воздействий в виде вибраций, ударов и линейных ускорений, которые могут приводить к ее механическим поломкам.

Для автоматизированного проектирования виброударонадежных конструкций блоков РЭА необходимы критерии оптимальности и методы по поиску оптимальных средств (из заданного набора) и их параметров для доведения механических режимов печатных узлов (ПУ) и элементов несущей конструкции до допустимого уровня, обеспечивающего требуемую надежность. Методы должны оптимально решать следующие функциональные задачи: определение габаритов печатных плат; определение расположения мест крепления ПУ; рекомендовать места размещения электрорадиоизделий (ЭРИ) и ребер жесткости на печатной плате; определять параметры мини-виброизоляторов для печатных узлов; определять параметры элементов несущей конструкции; вырабатывать требования к системе виброудароизоляции РЭА в целом в случае неудовлетворительных динамических механических характеристик конструкции.

В данной работе рассматривается разработанный метод оптимального расположения стоек и мест крепления печатных узлов в этажерочных конструкциях (ЭК) РЭА, которые являются наиболее распространенным типом конструкций, используемым в бортовых РЭА, подверженных интенсивным внешним виброударным механическим воздействиям. Конструкции этажерочного типа представляют собой несколько печатных узлов, соединенных металлическими стойками. Данный метод улучшения динамических характеристик конструкций является мало затратным, т.к. не требует больших изменений в конструкции.

Имеющиеся варианты решения

Существующие в настоящее время методы выбора расположения стоек и мест крепления ПУ основаны на опыте конструктора и последующем проверочном моделировании на ЭВМ, что не обеспечивает нахождение оптимального проектного решения, при котором вибрационные перегрузки на ЭРИ будут минимальны. Создание программного приложения по оптимизации расположения стоек и мест крепления печатных узлов наталкивается на большие вычислительные затраты, связанные с многократным расчетом амплитудно-частотных характеристик ПУ, входящих в состав ЭК.

Предлагаемый метод

Для экономии вычислительных затрат была построена макромодель динамики этажерочной конструкции в частотной области на основе метода конечных элементов (МКЭ) и метода электромеханической аналогии. Результатом применения МКЭ является система уравнений колебаний конструкции РЭА [1]:

{ |R| - ω²|M| + jω|C| } |δ| = |F|,

где:

• |R| – глобальная матрица жесткости;
• |M| – диагональная глобальная матрица масс;
• |δ| – вектор перемещений;
• |F| – вектор внешних воздействий;
• ω – круговая частота вибрации;
• j – мнимая единица, j = -1;
• |С| – глобальная матрица демпфирования.

Решение этой системы уравнений дает значения перемещений в узлах модели, что позволит определить реакцию конструкции РЭА на внешние воздействия: перегрузки на ЭРИ и механические напряжения в элементах конструкции.

Основной характеристикой вибрационных свойств конструкции является ее амплитудно-частотная характеристика (АЧХ), отражающая зависимость коэффициента динамичности от частоты вибрации. Для конструкций ПУ коэффициентом динамичности K_g является коэффициент отношения амплитуды ускорения (А_т) в точке конструкции к амплитуде ускорения в местах крепления ПУ (А_кр):

K_g = A_т/A_кр

По АЧХ конструкции ПУ можно определить резонансные частоты и коэффициенты динамичности, т.е. условия работы элементов, установленных в данной точке ПУ в части механических воздействий при гармоническом и случайном вибрационном воздействии, а также механический режим конструкции при ударном воздействии.

Резонансные частоты конструкции определяются жесткостью конструкции и массовой нагрузкой. В свою очередь, жесткость конструкции ПУ при прочих равных условиях зависит от количества и расположения узлов его крепления к несущей конструкции. Поэтому изменение расположения узлов крепления ПУ позволяет изменять его АЧХ. При изменении АЧХ за счет изменения расположения узлов крепления можно добиться уменьшения перегрузок на ЭРИ, если сместить резонансные частоты ПУ в частотную область, в которой внешнее воздействие меньше по сравнению с исходной областью воздействия.

Для ПУ наиболее опасными являются механические воздействия, поперечные к плоскости платы, т.к. в поперечном направлении возникают собственные частоты колебаний, попадающие в частотный диапазон внешних вибрационных воздействий. Это приводит к резонансным явлениям в ПУ и, следовательно, к увеличению амплитуды колебаний ПУ в десятки раз по сравнению с воздействующей амплитудой.

При механическом воздействии в поперечном к плоскости платы направлении через стойки вибрация передается от места воздействия до плат практически без изменений вследствие большой жесткости стоек при растяжении-сжатии. Это позволяет рассматривать ЭК при воздействии в поперечном направлении как группу независимых друг от друга конструкций ПУ, которые подвержены одинаковому воздействию.

При оптимизации конструкции ПУ, подверженного внешнему вибрационному воздействию, необходимо снизить перегрузки на ЭРИ, что можно сделать, изменив его АЧХ в сторону непопадания собственных частот колебаний ПУ в частотные диапазоны с большими значениями параметров воздействующей вибрации. Оптимизация конструкции ПУ путем нахождения оптимального расположения его узлов крепления состоит в переборе вариантов их расположения, расчете АЧХ для каждого варианта и выборе варианта, при котором перегрузки на ЭРИ удовлетворяют требованиям к ним. Многочисленный расчет АЧХ ЭК с использованием ее полной модели большой размерности (тысячи уравнений) традиционным методом шагами по частоте является трудоемким с точки зрения затрат машинного времени, поэтому предлагается экономичный метод моделирования ЭК в частотной области, основанный на построении макромодели ЭК, размерность которой равна лишь количеству варьируемых параметров и в ней имеется аналитическая зависимость АЧХ от частоты воздействующей вибрации. Количество варьируемых параметров равно количеству переставляемых узлов крепления, которое обычно составляет от 4 до 11.

Построение модели основано на электромеханической аналогии первого типа, в которой существует следующее соответствие между электрическими и механическими величинами: ток – скорость, индуктивность – масса, емкость – податливость (величина, обратная жесткости), активное сопротивление – коэффициент трения (вязкость). При переходе к эквивалентной электрической схеме в уравнении колебаний конструкции по методу конечных элементов производим следующие замены: матрицу масс заменяем на матрицу индуктивностей, матрицу демпфирования заменяем на матрицу активных сопротивлений, матрицу жесткостей заменяем на матрицу емкостей, обратных соответствующим жесткостям. Далее переходим к построению макромодели полученной электрической схемы.

Рассмотрим исходную модель электрической схемы в частотной области, построенную в расширенном однородном координатном базисе:

где:

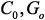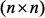• – -исходные вещественные матрицы коэффициентов;
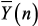• – вектор возмущающих воздействий;
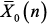• – искомый исходный вектор напряжений в узлах схемы и токов через индуктивности;
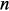• – количество неизвестных;
• ;
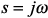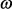•  – круговая частота;
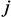• – мнимая единица.

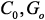При анализе чувствительности схем к большим изменениям параметров ЭРИ, от значений которых зависят коэффициенты матриц , параметр может изменяться от нуля до бесконечности, что позволяет варьировать структурой схемы, подключая или отключая элементы, т.е. узлы крепления, которым соответствует подключение индуктивностей, по величине на порядки больше массы ПУ и к которым прикладывается воздействующая сила в виде гармонического источника тока.

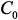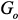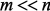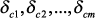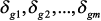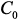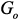Определим сначала чувствительность выходной характеристики к изменению параметров матриц и . Пусть варьируются параметров (m – равно количеству возможных мест крепления ПУ, которые в модели моделируются включением индуктивностей в соответствующие узлы), и они изменяются на величину или в матрицах и соответственно, а также в различных возможных вариантах.

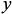Проводимость ветви – (или ее сопротивление), включенная между 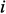и 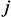узлами, появляется в матрице 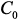и 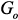в столбцах и строках с номерам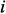и и 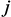, при этом имеет знак плюс в диагональных элементах 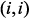и 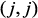и знак минус во внедиагональных элементах 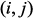и 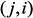. Эту зависимость можно записать, например, для матрицы 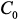в форме произведения векторов: 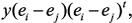где 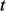– индекс транспонирования, 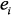– единичный вектор, все компоненты которого, кроме 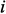, равны нулю, а 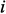равен единице, 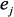– единичный вектор, все компоненты которого, кроме 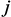, равны нулю, а 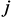равен единице [2].

Тогда матрица .

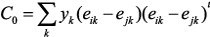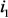Для четырехполюсников, имеющих два входных узла и 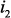и два выходных узла 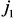и 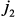, элемент матрицы 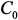, равный y, можно записать в виде: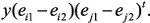

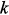Для четырехполюсника алгоритм занесения 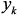в матрицу 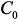(или 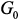) можно записать в виде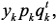
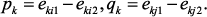
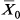где

Выходную величину представим в виде элементов вектора  , где 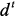– диагональная матрица, в диагонали которой находятся единицы в тех строках, номера которых равны номерам узлов выходных характеристик, а остальные элементы равны нулю;
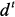– определяет номер элемента вектора 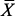, являющегося выходной характеристикой 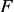при измененных параметрах: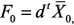

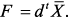
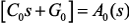Обозначим , при этом 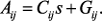Тогда при изменении параметров можно записать:

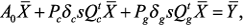(1)

где

,
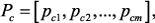
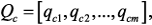
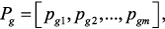
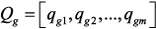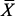– вектор решения при измененных параметрах, 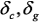– диагональные матрицы 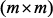изменений параметров.

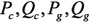Матрицы содержат информацию об адресах и знаках внесения параметров элементов в матрицу 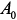, имеют размерность n x m и содержат нули и .

Обозначим

Уравнение (1) представим в виде системы уравнений:

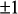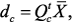
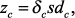
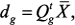
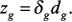
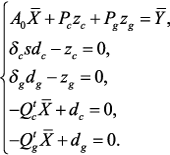(2)

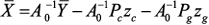Подставив из (1) в систему (2) и исключив из нее путем подстановк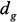и и 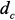, получим систему уравнений макромодели:

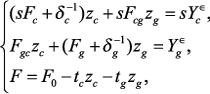(3)

где: .

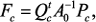
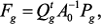
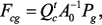
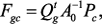
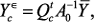
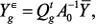
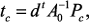
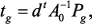
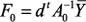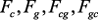В системе уравнений (3) матрицы имеют размерность 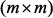, а векторы, 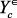, , 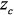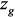и строки 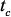, 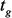– размер-ность .

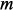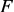Для того чтобы в выражении для сохранить аналитическую зависимость от 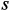, вычисление 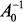производится по известному методу Н.И. Борисова [3], основанному на вычислении собственных значений 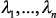матрицы 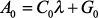и всех ее правых 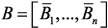и левых 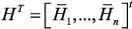собственных векторов, связанных условием нормировки 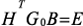, где 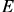– 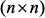единичная матрица. В результате матрица 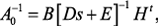где.

Эффективность метода

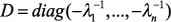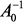Таким образом, вычислив один раз в виде аналитической зависимости от 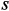и подставив в систему (3), имеющую размерность 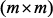, можно вычислять выходную характеристику 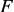на различных 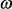при больших изменениях 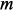параметров, т.е. индуктивностей, моделирующих места крепления ПУ.

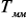Оценка предлагаемого метода произведена из сравнения вычислительных затрат на формирование макромодели (), вычисления выходной характеристики по исходной системе с симметричной положительно определенной матрицей коэффициентов (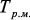) и полученной макромодели ():

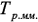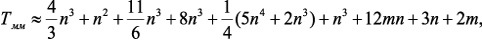
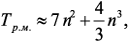
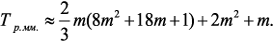
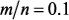Вычислительные затраты определялись в вещественных мульти­пликативных операциях. Из анализа приведенных выражений установлено, что при сокращение трудоемкости вычислений по макромодели 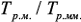будет не менее двух порядков, а построение макромодели оправдано, если надо сделать более десяти ша­гов оптимизации. Так, например, при 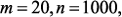количестве частотных точек – 100, количестве циклов оптимизации – 100, время решения при использовании макромоделирования (с учетом трудоемкости построения макромодели) уменьшилось в 42 раза по сравнению с решением при использовании полной модели.

Краткий алгоритм программы

Критерием оптимальности при перестановке мест крепления является минимум максимальной перегрузки на ЭРИ ЭК в заданном частотном диапазоне вибрации.

Алгоритм оптимизации расположения мест крепления ПУ ЭК состоит из следующих этапов:

• Ввод исходных данных с описанием конструкции, начальным и разрешенным расположением мест крепления, параметров внешних вибрационных воздействий.
• Построение макромодели колебаний конструкции в частотной области.
• Организация перестановки мест крепления, вычисление АЧХ по макромодели и критерия оптимальности при каждой перестановке, запоминание уменьшенного критерия оптимальности и соответствующего ему варианта перестановки.
• Вывод результатов.

1. Зенкевич О.К. Метод конечных элементов в технике/ пер.с англ. – М.: «Мир», 1975. – 541с.
2. Влах И., Сингхал К. Машинные методы анализа и проектирования электронных схем/ пер. с англ. – М.: «Радио и связь», 1988. – 560 с.
3. Борисов Н.И. Исследование и разработка методов снижения размерности и трудоемкости задач анализа и оптимизации линейных эквивалентных электрических схем на основе макромоделирования в САПР / Дисс. докт. техн. наук. – М.: МИЭМ, 1996. – 207с.

Ключевые слова: радиоэлектронная аппаратура, этажерочная конструкция, вибрация, макромодель, оптимизация.

The mathematical macro model vibration of the stacked bar construction of electronic equipment

Kogevnikov A.M., Tumkovskiy S.R.

National Research University «Higher School of Economics»

Summary: In this paper the method of constructing a macro model the dynamics of stacked bar construction of electronic equipment in the frequency domain based on the finite element method and electromechanical analogy.

Macro model has a dimension equal to the number of variable parameters in the optimization process. This greatly reduces the time optimization with a small number of variable parameters.

Keywords: electronic equipment; vibration, macro model, optimization.

Комментарии могут оставлять только зарегистрированные пользователи