 |
|
|
|||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Методы борьбы с омонимией Сейчас кажется привычной возможность задать вопрос любимой поисковой системе и моментально получить от нее соответствующий ответ. Для пользователя процесс может показаться простым, в то время как поисковый алгоритм встречает несколько препятствий, среди которых важное место занимает языковой барьер: вопрос, как правило, задается на естественном языке, которому, в отличие от компьютерного языка поискового алгоритма, присуща неоднозначность. Неоднозначными являются как тексты, в которых производится поиск, так и запрос пользователя. В этой статье пойдет речь о средствах снятия неоднозначности при автоматической обработке текста (и не обязательно при информационном поиске) О неоднозначности В этой статье мы будем говорить об омонимии, явлении, при котором у слова или разных слов совпадают некоторые формы. Если быть более точным, то можно выделить несколько видов омонимов:
Поскольку универсальной системы описания морфологии не существует, можно найти морфологические словари, отличающиеся разными наборами падежей или частей речи. По этой причине представления об омонимии (неоднозначности) для разных словарей могут немного отличаться. Наряду с морфологическими словарями существуют целые сборники текстов с разметкой, которые называются корпусами. В зависимости от корпуса разметка может включать не только морфологические, но также семантические и синтаксические характеристики [1]. Удобство доступа к информации делает корпус отличным источником статистических данных о языке – к примеру, можно узнать, какие виды неоднозначности являются наиболее распространенными. В таблице 1 отражена такая статистика согласно русскоязычным корпусам СинТагРус [2] и OpenCorpora [3]. Таблица 1. Статистика омонимии в русском языке
Нетрудно заметить, что содержание неоднозначности в разных корпусах тоже разное. В первую очередь это связано с использованием различных моделей морфологии, чуть меньшую роль играют стилистика текстов и объем данных. В одном корпуса едины: внушительная доля слов в русском языке обладает тем или иным видом омонимии. И как же с ней справиться? Машинное обучение Итак, чтобы устранить омонимию, каждое слово нужно «классифицировать», т.е. сопоставить ему лемму, часть речи и набор морфологических характеристик, которые для удобства объединяются в один тег. Для того чтобы узнать все возможные теги, достаточно найти все упоминания слова в имеющемся морфологическом словаре или использовать морфологический анализатор наподобие MyStem [4], который пытается предсказать теги слова. Остается только выбрать среди нескольких тегов единственный верный. С решением этой задачи может помочь машинное обучение, а конкретно – методы классификации. Перед началом работы классификатор необходимо обучить на реальных примерах, которые находятся в размеченном корпусе. Обучение заключается в определении связи между признаками объекта (часть речи соседних слов, капитализация, пунктуация) и классом (тегом). Конкретная реализация будет зависеть от выбранного метода. Виды методов Исторически сложилось так, что почти все методы снятия омонимии (т.е. устранения неоднозначности) делятся на две группы:
У каждой из этих групп есть свои достоинства и свои недостатки. Как часто бывает в таких ситуациях, сочетание в одном методе признаков (и достоинств) обеих групп может показать лучший результат по сравнению с ранее достигнутыми. Прежде чем ознакомиться с подобным гибридным методом, стоит рассмотреть представителей каждого вида. Правила: метод Брилля Показательным примером метода с автоматической генерацией правил является метод американского лингвиста Эрика Брилля. Обучение методу выглядит следующим образом:
Правила трансформации представляют собой набор «старый тег, новый тег, условие», а применение правила заключается в замене старого тега на новый при выполнении указанного условия. Минусом данного метода является падение роста точности с ростом числа правил [5], что, впрочем, согласуется с принципом Парето: «80% усилий обеспечивают 20% результата». В то же время принцип работает и в обратную сторону: выполнения одного только шага инициализации достаточно для достижения высокой точности снятия омонимии. Как показали тесты, проведенные на корпусе СинТагРус, метод позволяет определить часть речи каждого слова с точностью 97,4%, а полный набор морфологических характеристик – с точностью 87,6%. Согласно таблице 1 почти половина слов в корпусе СинТагРус не является омонимичными. Это значит, что в их случае верное определение части речи и морфологических характеристик является заслугой не метода снятия омонимии, а морфологического словаря/анализатора. Чтобы оценить фактическую полезную работу метода, нужно считать статистику не на всех словах, а только на омонимах. Выходит, что задача определения части речи ставится только для 24,10% корпуса, а определения части речи и морфологических характеристик – для 51,94%. Для вышеописанного частотного метода, являющегося сокращенной версией метода Брилля, полезная точность составляет 89,1 и 76,2% для части речи и морфологических характеристик соответственно. Статистика: скрытая марковская модель Статистические методы снятия омонимии позволяют рассчитать вероятность каждого возможного варианта на основе статистики встречаемости: если в каком-либо контексте существительное встречается чаще, чем союз, то омоним, встреченный в том же контексте, будет с большей вероятностью существительным, нежели союзом (если эти варианты допускает словарь). Для описания контекста пригодится N-грамма – один из математических инструментов, который широко используется в автоматической обработке текстов. N-грамма представляет собой последовательность из N однотипных элементов, будь то слова или теги. Такие последовательности из двух и трех элементов для удобства называют соответственно биграммами и триграммами. К примеру, биграмма вида (пред, сущ) описывает ситуацию, в которой перед существительным стоит предлог. Для удобства описания простейшего статистического метода снятия омонимии и всех последующих методов будут использоваться следующие обозначения:
Работа статистического метода снятия омонимии на основе скрытой марковской модели заключается в поиске наиболее вероятной последовательности тегов T = {T1,T2,...,Tn}, где Ti ∈ D(wi), а n – длина предложения. Если взять для примера подход наивного байесовского классификатора, то вероятность последовательности будет рассчитываться как произведение вероятностей ее отдельных биграмм. Наивность классификатора здесь заключается в предположении о том, что эти отдельные вероятности никак не зависят друг от друга. Итак, условие поиска записывается как:
Модификации модели Поскольку расчет вероятности основан на статистике встречаемости в корпусе, случается так, что вероятность P для некоторой редкой пары тегов равна нулю. Эта вроде бы небольшая погрешность может привести к тому, что все произведение последовательности независимо от остальных вероятностей обратится в ноль. Чтобы нивелировать этот недостаток, в статистике используется так называемое сглаживание. Наглядный пример сглаживания Лапласа в функции P, гарантирующий, что ее значение будет строго больше нуля, может выглядеть следующим образом:
Разумеется, сглаживание – не панацея, поэтому чрезмерно полагаться на него не стоит. Чем больше корпус и чем меньше пространство признаков, тем больше доверия к собранным данным и меньше вероятность, что какое-либо редкое сочетание было пропущено [6]. Обычно размер корпуса фиксирован, зато имеется полная свобода выбора признаков для сбора статистики. К примеру, вместо биграмм можно учитывать триграммы. Формула поиска в этом случае примет вид:
где
В качестве альтернативы, к признакам можно добавить пунктуацию, но тогда встанет вопрос о том, каким образом она будет учитываться в N-граммах. Например, если считать пунктуацию отдельным тегом, из статистики биграмм пропадут пары тегов, которые разделяет какой-либо из знаков пунктуации. Чтобы сохранить эти связи, можно заменить биграммы (тег, тег) на триграммы (тег, пунктуация, тег). Тогда условие поиска станет выглядеть так:
а pmi – знак пунктуации после i-того слова. Здесь и в предыдущих примерах знаменатель может иметь другой вид, если он одинаков для всех цепочек в любой позиции i и таким образом не влияет на поиск максимума. Ничто не мешает использовать в качестве признаков слова, как это происходит в частотной модели. Как показала практика, использование в скрытой марковской модели данных о частоте тегов позволяет получить точность, недостижимую для этих моделей по отдельности. Формула поиска в случае использования биграмм без пунктуации будет выглядеть следующим образом:
Можно сделать статистику более конкретной, разбив все слова на отдельные группы. Для этого вводится функция G(w), сопоставляющая каждому слову идентификатор группы, к которой он относится. С вводом групп функция P примет вид:
где gi = G (wi), а Cg обозначает число n-грамм, в которых последнее слово относится к группе g. В зависимости от выбора принципа, по которому группируются слова, можно как повысить, так и понизить точность работы метода. В предлагаемой автором модификации каждой группе соответствует список вариантов тега, которые может принимать слово, другими словами, G(w) = D(w). В результате формула поиска становится такой:
Отдельного упоминания заслуживает реализация механизма работы метода. Казалось бы, можно двигаться от первого слова к последнему и выбирать наиболее вероятный тег с учетом соседей слева, однако этот подход вовсе не гарантирует, что полное произведение вероятностей будет максимальным из всех возможных. Для полной уверенности стоит перебрать абсолютно все варианты последовательностей, но поскольку каждое неоднозначное слово увеличивает число вариантов как минимум вдвое (а точнее, в |D(w)| раз), их общее число экспоненциально зависит от длины предложения, так что полный перебор не представляется возможным (или по крайней мере эффективным). К счастью, существуют методы динамического программирования, которые заключаются в рекурсивном разбиении сложной задачи на подзадачи, после чего из решений подзадач составляется общее решение. С их помощью можно найти последовательность с максимальной вероятностью за линейное, а не экспоненциальное время. Распространенными примерами методов динамического программирования являются алгоритм Витерби и алгоритм прямого-обратного хода. Динамическое программирование Для нахождения самых вероятных последовательностей в скрытых марковских моделях был разработан алгоритм Витерби, логика работы которого заключается в следующем: прежде чем найти наиболее вероятную последовательность тегов {T1,...,Tn}, нужно знать наиболее вероятные последовательности {T1,...,Tn-1}, тем, в свою очередь, нужны последовательности на один элемент короче, и так далее до простейшей последовательности {T1}, с которой и начнется вычисление. Таким образом, на любом этапе расчета s будут храниться не все возможные варианты Под алгоритмом прямого-обратного хода обычно понимается метод, работающий с временными последовательностями, но этот термин также применяют к алгоритмам, вычисляющим кроме прямых вероятностей P еще и обратные. Функция обратной вероятности P' для биграмм будет выглядеть следующим образом:
По аналогии с прямой вероятностью при i = n функция P' покажет вероятность того, что тег tn является последним в предложении. Итак, формула поиска приобретет вид:
Разумеется, ничто не запрещает сочетать любые из представленных модификаций, используя разные способы сглаживания, представления пунктуации, частот слов, учета групп и обратных вероятностей. Более того, можно перед снятием полной омонимии (т.е. определением морфологических характеристик) снять омонимию частеречную – найти части речи всех слов в предложении. В таблице 2 представлено сравнение некоторых вариантов, реализованных автором. Таблица 2. Статистика работы методов снятия омонимии на корпусе СинТагРус
* Эти методы показали лучшие результаты без применения сглаживания. **Точность с предварительным устранением частеречной омонимии.
Обучение рассмотренных выше методов заключается в простом сборе статистики. На ее основе не делается никаких выводов о связях между тегами и входными параметрами, остается лишь надеяться, что именно у правильного варианта разбора окажется наибольшая вероятность и алгоритм выберет его. В арсенале машинного обучения есть более «разумные» методы, к числу которых относится дерево принятия решений. Дерево принятия решений На этапе обучения дерево принимает весь список примеров вида (атрибуты, класс). Класс в нашей задаче соответствует тегу, а к атрибутам относятся морфологические характеристики слова и его соседей, знаки препинания и др. Выбирается один из атрибутов и помещается в текущую вершину дерева. Для каждого из значений атрибута строится поддерево, которому передается часть списка параметров, в котором атрибут принимает конкретно это значение. Поддеревья строятся рекурсивно до тех пор, пока не произойдет одно из двух событий:
Большое влияние на форму и качество работы дерева оказывает критерий, по которому в каждой вершине выбирается атрибут. К наиболее распространенным относятся следующие:
Теперь, когда обучение завершено, дерево готово к принятию решений. Работа дерева выглядит следующим образом:
Дерево принятия решений отлично работает с любым числом входных параметров, поскольку на каждом этапе построения критерий выберет только самый оптимальный из них. Кроме того, каждое решение можно легко объяснить, проследив маршрут от корня дерева до вершины, сделавшей выбор. Важным недостатком является так называемое переобучение – дерево учитывает конкретные особенности обучающей выборки, поэтому в незнакомом примере способно допустить грубую ошибку. Чтобы избежать переобучения, можно использовать метод подрезки, при котором убираются вершины дерева, не оказывающие влияния на качество принятия решений. *** Как это было показано выше, для снятия омонимии могут применяться различные методы. В статье не был рассмотрен еще один подход, основанный на нейронных сетях. Их плюсом является поиск скрытых зависимостей. Но для обучения любого подхода (кроме составления правил вручную) требуется размеченный корпус со снятой омонимией, причем желательно, чтобы омонимия снималась вручную. На практике проще взять один из существующих на данный момент словарей, открытых программных модулей снятия омонимии, размеченных корпусов и… И убедиться, что они несовместимы между собой. Собственно, именно поэтому создаются новые и новые решения в этой области.
Ключевые слова: компьютерная лингвистика, омонимия, частеречная разметка, скрытая марковская модель, машинное обучение. How to Kill Homonymy? Rysakov S.V., a graduate student of HSE, Department of Computer Engineering MIEM, rysakov.2009@itas.miem.edu.ru Summary: The article provides a review of modern methods of morphological ambiguity resolution. We considered such methods as statistical disambiguation, Brill’s automatically generated rules, de-cision trees and their modifications. For the comparison, the article provides numerical results ob-tained on two open corpora: OpenCorpora and SynTagRus. Keywords: computer linguistics, homonymy, POS-tagging, hidden Markov model, machine learn-ing. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 РЫСАКОВ С.В., аспирант НИУ ВШЭ, департамент компьютерной инженерии МИЭМ,
РЫСАКОВ С.В., аспирант НИУ ВШЭ, департамент компьютерной инженерии МИЭМ, 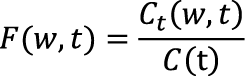
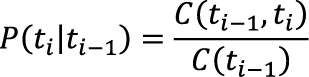
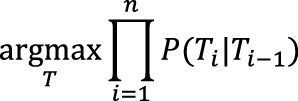
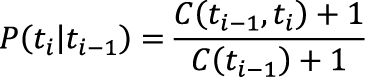
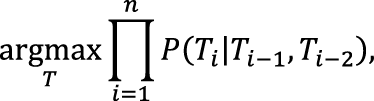
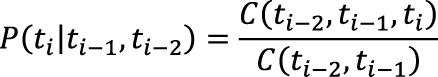
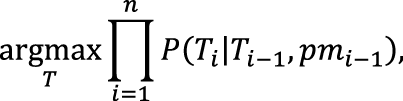
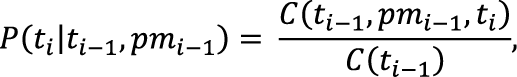
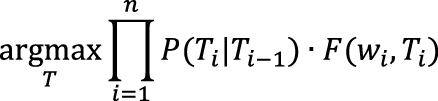
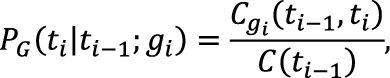
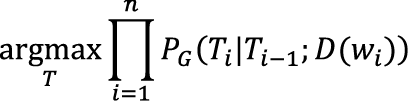
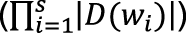 , а только наиболее вероятные (|D(ws)|). Это также означает, что в этапах с однозначным словом остается только один (самый вероятный) вариант, определяющий все теги для пройденной части предложения.
, а только наиболее вероятные (|D(ws)|). Это также означает, что в этапах с однозначным словом остается только один (самый вероятный) вариант, определяющий все теги для пройденной части предложения.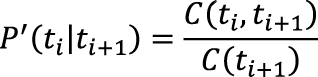
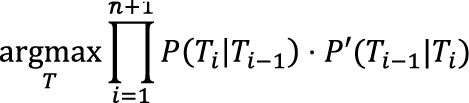
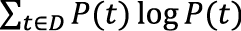 , где D – множество всех тегов, а P(t) – отношение количества примеров с тегом t к количеству всех примеров.
, где D – множество всех тегов, а P(t) – отношение количества примеров с тегом t к количеству всех примеров.


