|
|
|
|||||||||||||
|
|
Комплекс информационного обеспечения принятия решений Важной научной и практической проблемой настоящего времени является решение задач построения различных параметрических и непараметрических систем управления динамическими объектами, в том числе как для принятия решений, так и для динамической реструктуризации [1-7]. Примерами этой проблемы в области науки и технологий являются управление критическими объектами производственных процессов и их испытание, диспетчеризация и выполнение процессов, управление в режиме разделения времени, складская логистика Одними из известных научных трудов, посвященных адаптивному управлению стохастическими системами с конечным множеством управляющих воздействий, являются [1-4]. В этих работах начато решение задач построения адаптивных систем, когда априорные сведения о входных данных объекта управления. Решаемые при этом задачи могут обеспечить повышение эффективности методов адаптивного выбора вариантов. Предложены принципиально новые адаптивные алгоритмы поиска. Несмотря на это, нерешенной прежде частью общей проблемы, которой и посвящена данная публикация, является рассмотрение программного комплекса адаптивного выбора. Этот комплекс может быть пригоден для информационного обеспечения принятия решений в условиях априорной неопределенности входных данных. Целью данной работы является приведение результатов системного анализа программно-инструментального комплекса адаптивного принятия решений адаптивными алгоритмами. Разработанный комплекс позволяет решать задачи безусловной минимизации по критерию минимума предельных значений средних текущих потерь. Методы принятия решений Одной из принятых терминологий для описания автоматных рекуррентных последовательностей является та, что используется в работах [1, 2]. В соответствии с [1] при использовании автоматных оптимизационных алгоритмов непрерывное время функционирования объекта управления разбивается на последовательные интервалы длительности T, каждому из которых присваивается номер
где Перед выбором очередного варианта Известный [1, 2] метод деления отрезка состоит в том, что, если известно значение Пусть для любого
определяется условием Различают [1-4] беспроекционные алгоритмы адаптивного выбора вариантов вида Если
Считается [1-4], что проекционные алгоритмы объективно лучше беспроекционных за счет потенциала их использования для решения более обширного класса задач, чем беспроекционныме, по критериям (3), а именно при присутствии как бинарных, так и небинарных потерь Известные алгоритмы адаптивного выбора с приведением необходимых для описания рекуррентных последовательностей приведены в [1]. Стоит отметить, что для их сравнительной оценки, помимо использования данных реальных систем, можно ограничиться тестовой задачей [2], в которой число вариантов N=5, потери Автором настоящей работы предложены два принципиально новых стохастических метода и реализованы соответствующие им алгоритмы: проекционный алгоритм стохастической аппроксимации с использованием соседних вариантов для оптимизации управления выбором управляющих воздействий [6]; алгоритм доминирующего выбора вариантов для принятия решений в условиях вирусной атаки [7]. Необходимо подробнее остановиться на каждом из них. В проекционном алгоритме стохастической аппроксимации с использованием соседних вариантов [6] для оптимизации управления выбором управляющих воздействий рекуррентная формула разработанного автором алгоритма имеет вид:
В формуле (4) d обозначает абсолютное значение наибольшей величины разности между соседними элементами к выбранному в векторе вероятностей. Эти элементы получают некоторое, численно равное d, преимущество перед остальными, которое и обеспечивает использование соседних вариантов (соседние элементы получают условно более высокий ранг, при этом происходит разбиение множества совокупности элементов вектора на два – соседние и несоседние). Естественно, что когда выбранный элемент является первым или последним в векторе, то сосед у него всего лишь один. Формула (4) представлена в виде соответствия вычислительному процессу в программной реализации. Момент отличия предложенного алгоритма от разработки Назина–Позняка иллюстрируется на рис. 1, причем рис. 1а демонстрирует случай проекционного алгоритма, а рис. 1б – алгоритма по [6]. а Рисунок 1. Изменение вектора выбора вариантов (а – алгоритм Назина–Позняка, б – алгоритм [6]) В свою очередь, предлагаемый алгоритм выбора доминирующего варианта [7] функционирует следующим образом. Вначале происходят прогоны с фиксированным вариантом, номер варианта постоянен и равен номеру прогона. Затем происходит непосредственно функционирование, выбранным номером варианта является вариант, для которого имеется наименьшее значение среднего от средних величин текущих потерь. Если таких вариантов несколько, используется с наименьшим порядковым номером. Для последующего построения рекуррентной последовательности управляющих воздействий используется алгоритм Назина–Позняка [1]:
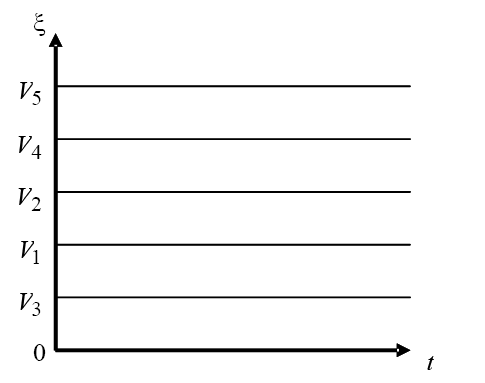
В (5) Для исследования работы алгоритма в силу того, что происходит управление выбором вариантов, разумно использовать тестовую задачу, в которой число вариантов N=5, а потери
Рисунок 2. Тестовая задача
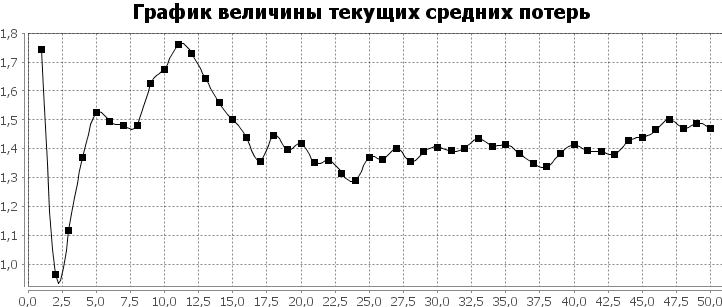
Программный комплекс информационного обеспечения принятия решений Программно-инструментальный комплекс для информационного обеспечения поддержки принятия решений обеспечивает решение задач адаптивного принятия решений автоматными алгоритмами. Они являются задачами безусловной минимизации по критерию минимума оценок значений предельных средних потерь. Пользователь выбирает алгоритм оптимизации, задает число шагов, параметры алгоритма и значения функции текущих потерь на каждом шаге оптимизации. Система получает для каждого шага алгоритма номер следующего варианта управления и величины текущих средних потерь. После завершения фазы оптимизации производится построение графика величины текущих средних потерь в зависимости от шага алгоритма, а также расчет описательной статистики для значений текущих средних потерь. Разработка ведется на языке программирования высокого уровня Java и с использованием библиотек Swing, Apache Commons Math, JFreeChart. Реализуются алгоритмы стохастической оптимизации:
При разработке программного средства, определения функциональных задач, декомпозиции системы на подсистемы и определения связей между ними используются принципы системного подхода. В соответствии с основополагающим принципом системного анализа, который называется принципом конечной цели, выделяются наиболее важные функции реализуемого программного комплекса: реализация одного шага алгоритмов оптимизации [1, 6, 7], получение бинарных и небинарных потерь, выбор варианта методом деления отрезка, выполнение оптимизации для заданного числа шагов и заданных параметров алгоритмов, расчет описательных статистик, обеспечение обработки ошибок и исключений, работа с визуальными компонентами и поддержка пользовательского интерфейса. По принципу единства комплекс рассматривается одновременно как целое и как совокупность элементов. Можно у комплекса выделить подсистемы, композиция которых вместе с взаимосвязями позволит выполнить все требуемые функции, а также определит структуру комплекса, а именно
В (6)
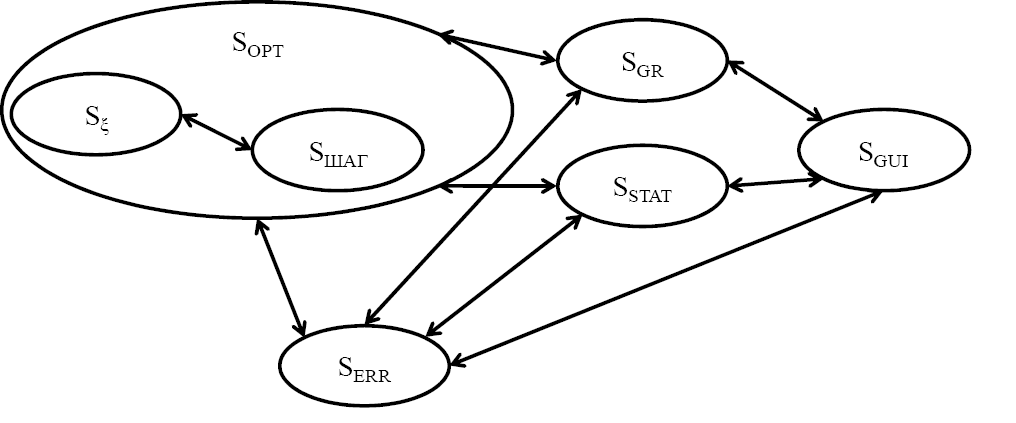
По принципу связности любая часть и подсистема комплекса должна рассматриваться вместе с взаимосвязями с другими подсистемами и окружающей операционной системой, аппаратным и программным обеспечением. По принципу модульности выделяются программные модули, реализующие (6). Используется объектно-ориентированное программирование, система классов повторяет и реализует (6). По принципу иерархии в комплексе реализованы иерархии подсистем. Эти связи с иерархиями наглядно представляются на рис. 3. Рисунок 3. Изображение связей подсистем
По принципу функциональности выделяются функции комплекса и его подсистем:
В (7)
По принципу развития имеется возможность дальнейшего совершенствования комплекса путем добавления новых алгоритмов и методов для выполнения безусловной минимизации по критерию минимума средних значений оценок текущих потерь. По принципу сочетания централизации и децентрализации степень централизации минимальна, а именно отдельные Java-классы могут использоваться независимо в других программных продуктах. По принципу учета неопределенности и случайностей учитывается возможность возникновения ошибок, как внутри комплекса, так и со стороны операционной системы и используемых аппаратных средств, принимаются необходимые меры для уменьшения возможных потерь данных и дальнейшего функционирования комплекса. Фрагменты интерфейса комплекса изображаются на рис. 4, 5. Рисунок 4. Фрагменты интерфейса программно-инструментального комплекса, а Рисунок 5. Фрагменты интерфейса программно-инструментального комплекса, б Вывод В работе предлагается описание программно-инструментального комплекса информационного обеспечения принятия решений при условии априорной неопределенности входных данных адаптивного принятия решений адаптивными алгоритмами. Комплекс позволяет решать задачи безусловной минимизации по критерию минимума предельных средних потерь. Перспективой дальнейших изысканий по данной тематике станет развитие программного комплекса с использованием принципов системного подхода.
Ключевые слова: поддержка принятия решений, априорная неопределенность, стохастические автоматы Complex information support of decision making under the condition of a priori indeterminacy of the input data Tkachenko Kirill Stanislavovich, 1st cat. Specialist on educational and methodical work, Assistant, Graduate student Federal State Budget Educational Institution of Higher Education «Sevastopol State University» Sevastopol, Russian Federation, 299053, tkachenkokirillstanislavovich@mail.ru, tkachenkokirillstanislavovich@gmail.com Summary: There are stochastic approximation method using neighboring variants to optimize the control actions choices and the dominant method of options selection for decision making suppor under conditions of virus attack provided in this article. Program-instrumental complex for informational decision making support under the condition of a priori uncertainty of the input data adaptive decision making stochastic automata algorithms described. Keywords: decision making support, a priori indeterminacy, stochastic automata. |
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 ТКАЧЕНКО К.С., аспирант, Федеральное государственное бюджетное образовательное учреждение высшего образования «Севастопольский государственный университет»,
ТКАЧЕНКО К.С., аспирант, Федеральное государственное бюджетное образовательное учреждение высшего образования «Севастопольский государственный университет», 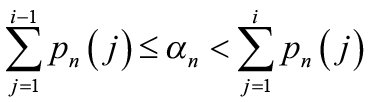 . Потому подход и называется рандомизированным. Удобно использовать обозначения:
. Потому подход и называется рандомизированным. Удобно использовать обозначения:  ;
; 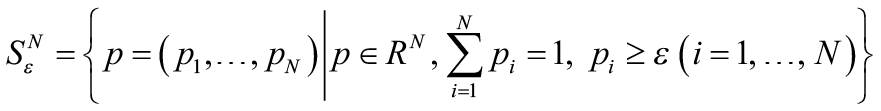 , (2)
, (2)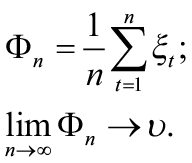 (3)
(3)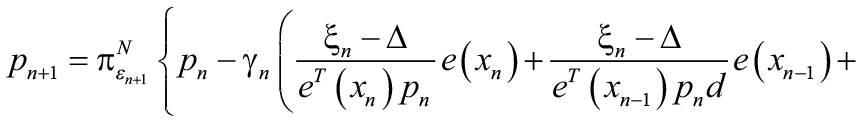
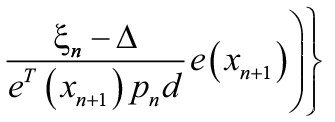 , (4)
, (4)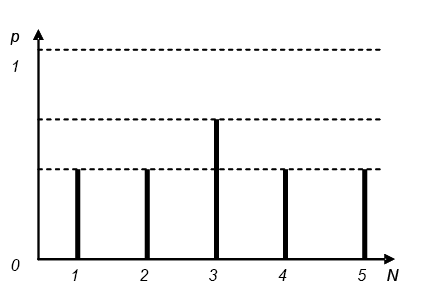 б
б ![Рисунок 1. Изменение вектора выбора вариантов (б – алгоритм [6]) Рисунок 1. Изменение вектора выбора вариантов (б – алгоритм [6])](../../../../uploads/articles/2015/07-08/134_137-Complex_Information_Support/image01b.png)
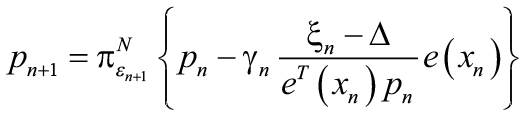 . (5)
. (5)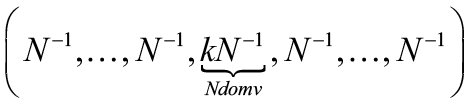 , где
, где