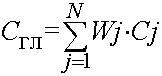Принятие решений при администрировании сложных технических проектов

  ВИШНЕКОВ А.В., д.т.н., профессор, avishnekov@hse.ru
 ИВАНОВА Е.М., к.т.н., доцент, emivanova@hse.ru

Департамент компьютерной инженерии Московского института электроники и математики Национального исследовательского университета «Высшая школа экономики», г. Москва

Принятие решений
при администрировании сложных технических проектов

В статье рассматриваются вопросы применения методов поддержки принятия решений при администрировании и выполнении сложных проектов. Приведены основные типы задач принятия решений. Исследования показали, что эти задачи имеют сложный и многокритериальный характер, при их решении лицо, принимающее решение (руководитель проекта, руководители проектных подразделений, инженеры-разработчики), может допустить ошибки. При выполнении сложных дорогостоящих проектов цена этих ошибок велика и может поставить под вопрос успешность проекта. Приводится пример применения метода последовательных уступок для решения задачи подбора персонала для выполнения проекта

Введение

В настоящее время перед отечественными предприятиями, работающими в сфере высоких технологий, ставится задача разработки конкурентоспособной продукции, включая различные виды программно-аппаратного обеспечения. Разработка должна вестись в соответствии с государственными отраслевыми стандартами с учетом многообразных критериев качества проектных решений.

Руководитель предприятия (проекта) в повседневной практике встречается с множеством задач принятия решений. Это выбор приоритетных проектов, схем их финансирования, выбор подрядчиков и поставщиков комплектующих материалов и программных средств, выбор наиболее рациональных проектных решений, кадровые решения и многое другое.

Постоянный рост многообразия и сложности решаемых задач требует необходимости владения современными методами и системами поддержки принятия решений. Эти задачи, как правило, носят слабо структурированный и неструктурированный характер, требуют учета большого объема разнородной информации и могут быть отнесены к задачам принятия решений в условиях многокритериальности. Число ихарактер критериев оценки качества принимаемых решений зависят от конкретики решаемой задачи. Их число может быть большим и малым, они могут иметь численный и лингвистический характер. Число возможных альтернативных решений поставленной задачи также может быть различным: от единиц до сотен. Поэтому часто взвешенное принятие того или иного решения является сложной и весьма трудоемкой задачей для руководителя. Применение на практике методов поддержки принятия решений может значительно облегчить подобную работу и автоматизировать ее.

Сегодня к методам поддержки принятия решений относят чуть ли не все возможные методы получения информации, помогающей человеку принимать те или иные решения (системы Big Data [1], BI системы [2], информационные системы). Однако более корректно относить к данным методам методы, имеющие непосредственное отношение к теории принятия решений [3]. Поэтому под методами поддержки принятия решений будем понимать методы, представляющие собой последовательность человеко-машинных процедур, позволяющих заменить сложную для человека (по данным психологических исследований [4]) процедуру многокритериального выбора на последовательность «элементарных» процедур, при выполнении которых человек, как правило, не совершает ошибок. К типовым процедурам, используемым лицом, принимающим решения (ЛПР), можно отнести:

• Сравнение оценок двух критериев (определение превосходства одного из них).
• Сравнение оценок двух альтернатив по шкале оного критерия (определение превосходства одной из них).
• Определение удовлетворительного значения для оценки альтернативы по какому-либо критерию.
• Выделение всех или части критериев, оценки по которым должны быть улучшены, могут быть ухудшены либо остаться не хуже установленного уровня (совокупность процедур 1, 2).
• Выделение удовлетворительных и неудовлетворительных (в какой-то степени оценок) по заданным критериям.

Методы поддержки принятия решений направлены на сравнение преимущественно альтернатив, относящихся к множеству Эджворта–Порето (сложные для сравнения) [3], то есть таких, которые нельзя сравнить безпривлечения дополнительной информации от ЛПР (например, задание весов критериев оценки альтернатив). Использование методов поддержки принятия решений при администрировании сложных проектов обусловлено и тем, что руководитель (ЛПР) получает возможность поддержки принятия решений не только в условиях определенности исходной информации, но и в вероятностно-определенных условиях и вусловиях неопределенности. Это важно при запуске масштабных долговременных проектов, т.к. на момент начала выполнения проекта трудно точно сказать, какое состояние «внешней среды» будет на момент выполнения какого-либо из этапов проекта. Под состоянием внешней среды будем понимать совокупность внешних факторов, влияющих на значения критериев оценки вариантов проектных решений на конкретном этапе.

Различают две ситуации: можно рассчитать вероятность наступления возможных состояний «внешней среды», тогда говорят о принятии решений в вероятностно-определенных условиях, и когда вероятность наступления возможных состояний «внешней среды» рассчитать невозможно, тогда говорят о принятия решений в условиях неопределенности исходной информации.

Постановка задачи

В самом общем виде задача принятия решений может выглядеть следующим образом. Задано множество альтернатив (возможных вариантов решения) или область допустимых значений параметров альтернатив имножество критериев оценки качества заданных альтернатив. Необходимо решить одну из следующих задач: выбор наиболее рационального решения, ранжирование альтернатив по степени предпочтения, группировка альтернатив по заданным признакам.

Руководитель проекта может самостоятельно решать одну из выше указанных задач (индивидуальное принятие решения) либо может привлечь группу экспертов (групповое принятие решений). Одной из задач, которые часто решает руководитель проекта, является задача подбора персонала для выполнения проектных работ.

В каждом конкретном случае критерии подбора персонала для выполнения проекта зависят от требуемой квалификации сотрудника [5]. Наименьшую сложность представляет подбор специалиста низкой квалификации, которого легко можно заменить. Гораздо сложнее найти высококлассного специалиста (директора, топ-менеджера, главного бухгалтера, ведущего инженера-проектировщика и др.), способного за счет своих уникальных знаний и личных качеств создавать для фирмы дорогостоящие продукты. Именно для перечисленных категорий кандидатов используются уникальные методики подбора персонала (тесты, деловые игры, многократные собеседования) и именно здесь можно значительно облегчить задачу руководителя, применив методы поддержки принятия решений.

К специалистам высокой квалификации современные работодатели предъявляют различные требования [5, 6], которые можно рассматривать как критерии подбора персонала:

• высшее образование (квалификация, соответствующая занимаемой должности);
• знание иностранных языков;
• опыт работы (время работы в данной должности);
• наличие некоторых дополнительных навыков (например, наличие водительского удостоверения определенной категории, умение использовать в работе ПК и оргтехнику);
• физические/медицинские характеристики, соответствующие напряженности и сложности выполняемых работ;
• деловые качества (коммуникабельность, честность, порядочность, деловитость);
• готовность работать ненормированный рабочий день;
• наличие и весомость рекомендации;
• персональные характеристики (пол, возраст, социальный статус, тип личности, семейное положение) и др.

В качестве альтернативных решений могут рассматриваться кандидатуры на рассматриваемую должность с их оценками по выбранным из предыдущего списка критериям.

Решение задачи подбора персонала методом последовательных уступок

Для решения подобных задач хорошо зарекомендовали себя методы, основанные на задании уступок на значения критериев оценки кандидатов, – метод STEM и метод последовательных уступок.

Французская компания SEMA для решения задачи подбора персонала использует метод STEM [3], содержащий фазу расчетов (оптимизации) и фазу анализа, на которой рассматривается вектор значений критериев, найденный при оптимизации по глобальному критерию:

где W_j – вес j-го критерия, а C_j – оценка кандидата по j-му критерию.

Затем выявляются критерии, оценки по которым являются неудовлетворительными, и для наименее удовлетворительного критерия назначается уступка (задается новое пороговое значение), и фаза расчетов (оптимизации) повторяется для новой области допустимых значений критериев. Если на очередном шаге значения всех критериев принимаются удовлетворительными, решение считается найденным.

Рассмотрим решение задачи выбора наилучшего кандидата для выполнения проекта с использованием метода последовательных уступок [3].

Первый шаг применения метода последовательных уступок заключается в том, что следует определить частные критерии отбора персонала для указанной должности. Допустим, что для отбора используются следующие пять критериев:

• образование (квалификация, соответствие рассматриваемой работе);
• опыт работы (время работы в данной должности);
• деловые качества (коммуникабельность, деловитость);
• готовность работать ненормированный рабочий день;
• наличие и весомость рекомендации.

Затем производится анализ относительной важности выбранных частных критериев отбора. Это может проделать ЛПР, рассчитав веса выбранных критериев с применением процедур попарного сравнения критериев из метода аналитических иерархий [3]. Также веса можно рассчитать, пригласив группу экспертов, применив групповые методы согласования экспертных решений, такие, например, как метод ранга [4].

Допустим, что для критериев К1-К5 были получены следующие веса:

• образование (вес 0,30);
• опыт работы (вес 0,10);
• деловые качества (вес 0,15);
• готовность работать ненормированный рабочий день (вес 0,25);
• наличие рекомендации (вес 0,20).

На основании этого анализа критерии располагаются в порядке убывания их важности. Допустим, что в нашем случае критерии были проранжированы следующим образом:

• К1. образование (W_К1=0,30);
• К2. готовность работать ненормированный рабочий день (W_К2=0,25);
• К3. наличие и весомость рекомендации (W_К3=0,20);
• К4. деловые качества (W_К4=0,15);
• К5. опыт работы (W_К5=0,10).

Следующий шаг применения метода последовательных уступок будет заключаться в том, что всем критериям следует определить допустимые значения, например, по 100-балльной шкале. Для каждого критерия определяются его максимально достижимое значение Q_j и величина «допустимого» снижения этого значения (уступки) D_j>0 для того, чтобы определить, удовлетворяет ли кандидат выставляемым требованиям.

На следующем шаге ЛПР оценивает всех кандидатов с применением выбранных критериев и расставляет оценки каждому i-му кандидату по каждому j-му критерию с применением той же 100-балльной шкалы. В результате если обнаруживается кандидат с максимальным значением критерия К1 и удовлетворяющий всем прочим критериям, то выбор сделан.

Если таковых кандидатов несколько, то сравниваются прочие оценки по другим критериям и выбирается кандидат с максимальными оценками по наиболее важным критериям.

Если таковые кандидаты отсутствуют, то организуется процедура решения многокритериальной задачи методом последовательных уступок. Метод заключается в том, что начиная с главного критерия К1 ипоследовательно задавая несколько небольших уступок в его значении можно найти кандидата, удовлетворяющего критерию К1 и всем прочим критериям. Из этих кандидатов можно выбрать одного с максимальными показателями по критерию К2. Если и таких кандидатов несколько, процедуру оптимизации следует продолжить для критерия К2, затем возможно К3 и т.д.

Пример решения задачи

Рассмотрим пример решения задачи подбора персонала методом последовательных уступок. Пусть имеется 10 кандидатов и пять выбранных критериев, предложенных выше. Допустим, ЛПР выставил численные оценки каждому кандидату по выбранным критериям отбора (см. таблицу 1), а также установил минимально допустимые оценки по каждому из критериев (см. таблицу 2).

Таблица 1. Оценки кандидатур

Таблица 2. Минимально допустимые значения оценки кандидатур по критериям

Оценки	Критерии Кj
	К1	К2	К3	К4	К5
Максимальная оценка (max() = Qj )	100	90	100	100	100
Минимальная оценка (Qj – Dj )	90	75	85	80	70
Максимальная уступка (Dj)	10	15	15	20	30

Первым шагом решения задачи будет поиск кандидатов с максимальным значением первого критерия: Q₁=100 . В нашем примере таких кандидатов два: А3 и А10 (см. таблицу 1). Для указанных кандидатов проверяем, удовлетворяют ли они следующему по важности критерию К2, и выясняем, что не удовлетворяют. Следовательно, необходимо использовать метод последовательных уступок начиная с предыдущего критерия К1.

На втором шаге решения многокритериальной задачи мы рассматриваем критерий К1 и задаем для него небольшую уступку =5 (т.е. новое максимальное значение критерия К1 равно =95 ) и проверяем, не появился ли удовлетворяющий новым условиям кандидат. Помимо уже известных А3 и А10, добавился кандидат А8, однако и он также не удовлетворяет критерию К2. Тогда предлагается сделать другую уступку =10 по критерию К1 (т.е. новое максимальное значение критерия К1 равно =90) и проверяем, не появился ли удовлетворяющий этим новым условиям кандидат. Таких кандидатов оказалось несколько: А2, А3, А4, А5, А6, А8, А10, но ни один из них не удовлетворяет критерию К2. Однако большую уступку по критерию К1 делать не имеет смысла, т.к. это наиболее важный из критериев, и работодатель (выступающий в роли ЛПР) не может поступиться своими требованиями.

Тогда на третьем шаге рассматриваем критерий К2. Его максимально достижимое значение: Q₂=90 . Задаем небольшую уступку =5 по критерию К2 (т.е. новое максимальное значение критерия К1 равно =85) и проверяем, не появился ли кандидат, удовлетворяющий новым условиям (=90 и =85). Таких кандидатов нет. Тогда задаем другую уступку =10 по критерию К2 (т.е. новое максимальное значение критерия К2 равно =80) и проводим еще одну проверку с минимальными условиями (=90 и =80). Таких кандидатов три: А3, А4, А5. Для них проверяем, удовлетворяют ли они критерию К3. Ни один из найденных кандидатов не соответствует условиям. Тогда задаем еще одну другую уступку =15 по критерию К2 (т.е. новое максимальное значение критерия К2 равно =75) и проводим еще одну проверку на соответствие кандидатов условиям (=90 и =75). Находим несколько кандидатов: А3, А4, А5, А6, А8 (см. таблицу 1), из которых никто не удовлетворяет критерию К3.

Большую уступку по критерию К2 делать нельзя, и мы на следующем шаге переходим к рассмотрению критерия К3. Его максимально достижимое значение: Q3=100 . Задаем небольшую уступку =5 покритерию К3 (т.е. новое максимальное значение критерия К3 равно =95) и проверяем, не появился ли кандидат, удовлетворяющий новым условиям (=90,  =75  и =95). Таких кандидатов нет. Тогда задаем другую уступку =10 по критерию К3 (т.е. новое максимальное значение критерия К3 равно =90) и проводим еще одну проверку с минимальными условиями (=90, =75 и =90). Таких кандидатов три: А5, А6, А8. Для них проверяем, удовлетворяют ли они критерию К4. Только кандидат А6 удовлетворяет нашим условиям, для него проверяем соответствие по критерию К5 – оно соблюдено. Утверждаем кандидата А6 как окончательное решение.

Заключение

В распоряжении руководителя проекта (при администрировании проекта) и исполнителей (при принятии проектных решений) должны быть средства, помогающие принимать наиболее рациональные решения. Необходимость подобных средств продиктована сложностью решаемых задач, их многоальтернативностью и многокритериальностью. Одним из наиболее эффективных средств является применение методов поддержки принятия решений. Выбор конкретного метода проводится на основе анализа решаемой задачи: использование численных или лингвистических критериев, число возможных альтернатив, число применяемых критериев оценки качества принимаемых решений, необходимость привлечения экспертов, возможные состояния «внешней среды», необходимость выбора единственного наиболее рационального решения или ранжирования возможных решений по степени их предпочтительности. Использование методов поддержки принятия решений позволит не только повысить качество и эффективность принимаемых решений, но и автоматизировать процесс принятия административных и проектных решений.

1. http://habrahabr.ru/hub/bigdata.
2. http://programmist1s.ru/bi-sistemyi.
3. Ларичев О.И. Теория и методы принятия решений. – 2-е изд., перераб. и доп. – М.: «Логос», 2002. – 392 с.
4. Ларичев О.И., Байченко В.С. и др. Проблемы выявления альтернатив и двоичных оценках на шкалах критериев//Многокритериальный выбор при решении слабоструктурированных проблем: Тр. ВНИИСИ, 1978, №5. – С.61-77.
5. http://www.kadry.ru/articles/detail.php?ID=1446.
6. http://center-yf.ru/data/Kadroviku/Kriterii-otbora-personala.php .
7. Иванова Е.М., Вишнеков А.В., Ерохин В.В. Автоматизация процедуры выбора микроконтроллера // Нано- и микросистемная техника, 2014, № 7. – С. 14-21.

Ключевые слова: администрирование проекта, задача принятия решения, методы поддержки принятия решений.

Decision making when administering complex technical projects

Vishnekov A.V., professor, avishnekov@hse.ru

Ivanova E. M., ass. professor, emivanova@hse.ru

National Research University Higher School of Economics, Moscow Institute of Electronics and Mathematics, «Computer Engineering» department, Moscow

Summary: The article deals with the application of decision support in the complex projects administration and execution. The main types of decision-making problems are shown. Research have shown that these problems have complex and multi-criteria character. The solution of this task by the decision-maker (project managers, design departments managers, design engineers) can cause some mistakes. When performing complex and expensive projects the price of these mistakes is high and may affect the success of the project. An example of the successive concessions method to solve the problem of recruitment for the project.

Keywords: project administration, the decision-making task, decision support methods.

Комментарии могут оставлять только зарегистрированные пользователи