|
|
|
|||||||||||||
|
|
Разработка и исследование программной системы Разрабатывается и исследуется программная система поддержки принятия решений с методом стохастической аппроксимации с выбором доминирующего варианта. Приводятся необходимые рисунки, таблицы Проблема проектирования, анализа, построения сложных компьютерных вычислительных систем, распределенных систем, сред и сетей является ключевым фактором обеспечения функционирования любой технической системы, в том числе при управлении объектами критического применения, а также системами реального времени. Эта проблема связана с научными и практическими задачами принятия решений и параметрического синтеза систем управления динамическими объектами. Одним из известных способов решения таких задач является использование при адаптивном управлении в условиях априорной неопределенности входных данных стохастических автоматов для выбора из конечного множества управляющих воздействий. Известными трудами, посвященными рассмотрению с единых позиций возможных решений задач безусловного и условного выбора, являются [1, 2]. Проектированию и использованию новых методов управления на основе рекуррентных последовательностей, как и решению возникающих при этом частных задач, посвящены публикации [3, 4, 5]. При этом нерешенной прежде частью общей проблемы, которая рассматривается в данной работе, является разработка методов управления с выбором доминирующего варианта и их реализаций. Цель этой статьи – построение метода управления на основе проекционного алгоритма стохастической оптимизации с возможностью выбора доминирующего варианта, с последующей разработкой и исследованием программной системы поддержки принятия решений, реализующей этот метод и алгоритм. Для обеспечения необходимого уровня надежности и безопасности функционирования, защиты от вирусных атак и несанкционированного доступа (в дальнейшем – ВА) в распределенных средах и системах, компьютерных системах и сетях, облачных и GRID-платформах (далее – РС) необходимо использовать программные средства поддержки принятия решений (СППР) в целях динамической реструктуризации обозначенных выше сложных технических систем. Это возможно по той причине, что РС по своей структуре, функциональной организации являются диверсионными. На достаточно высоком уровне абстракции структурная модель РС с СППР имеет вид, изображенный на рис. 1. Рисунок 1. Высокоуровневая абстрактная структурная модель РС с СППР Схему взаимодействия подсистем и информационных потоков между ними можно представить на рис. 2.
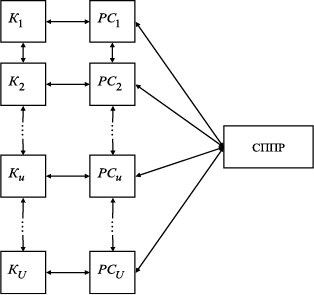
Рисунок 2. Схема взаимодействия подсистем Необходимо прокомментировать содержимое рис. 2 путем перечисления изображенных на нем объектов:
В целях некоторого упрощения явно предполагается, что число каналов тождественно равно числу информационно независимых структурных подразделений РС. Математической моделью РС с СППР в таком виде является граф:
В формуле (1) применяются обозначения:
РС с СППР выполняет большое количество функций, перечень которых удобно формализовать в виде множества:
В формуле (2):
Множество
В формуле (3):
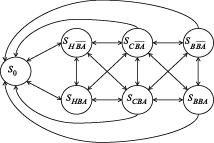
Для формулы (3) имеется наглядное изображение, представленное на рис. 3. Рисунок 3. Наглядное представление множества функций РС с СППР Для следующего этапа – построения графа состояний – необходим перечень состояний с указанием функциональной производительности системы и наличием ВА. Состояния, в которых может находиться система, сводятся в таблицу 1, а непосредственно граф состояний приводится на рис. 4. Таблица 1. Состояния, в которых может находиться система
Рисунок 4. Граф множества состояний Переходы между состояниями При этом для тривиального случая, в котором
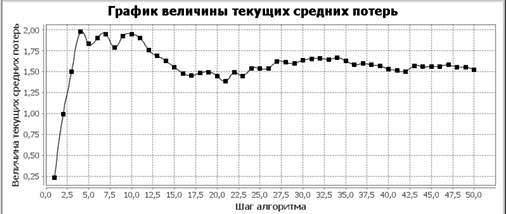
Но для построения такой последовательности можно использовать проекционные и беспроекторные алгоритмы стохастической аппроксимации. Прежде чем начать изложение разработанного алгоритма и метода, необходимо ввести обозначения. Пусть для любого Тогда так называемые рандомизированные стратегии используют рекуррентные правила вида Предлагаемый метод на основе алгоритма стохастической аппроксимации использует рекуррентное правило вида Задача безусловной минимизации предельных значений средних текущих потерь формулируется как Предлагаемый алгоритм функционирует следующим образом. Вначале происходят прогоны с фиксированным вариантом, номер варианта постоянен и равен номеру прогона. Затем происходит непосредственно функционирование, выбранным номером варианта является вариант, для которого имеется наименьшее значение среднего от средних величин текущих потерь. Если таких вариантов несколько, используется с наименьшим порядковым номером. Для последующего построения рекуррентной последовательности управляющих воздействий используется алгоритм Назина – Позняка с
В отличие от оригинального использования этого алгоритма начальными значениями компонентов вектора вероятностей выбора вариантов по (4) становятся Разработанное программное обеспечение СППР позволяет выполнять оптимизацию предложенным методом для рассмотренной выше модели РС. Результаты вычислительного эксперимента приводятся на рис. 5.
Рисунок 5. Результаты расчетов по предложенному методу Вывод. В результате исследования получен результат в области информационных систем и процессов. Перспективой дальнейших изысканий по данной тематике станет совершенствование разработанных моделей, методов и систем.
Ключевые слова: стохастическая аппроксимация, выбор доминирующего варианта, система поддержки принятия решений. Tkachenko Kirill Stanislavovich, 1st cat. Engineer, Graduate student, Federal State Budget Educational Institution of Higher Education «Sevastopol State University», tkachenkokirillstanislavovich@mail.ru, tkachenkokirillstanislavovich@gmail.com Development and research of the decision-making support software system with the method of dominant variant choice Developed and investigated the decision-making support software system with the method of stochastic approximation with dominant variant choice. The necessary drawings, tables provided. Keywords: stochastic approximation; dominant variant choice; decision support system. |
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 ТКАЧЕНКО К.С., инженер 1-й кат., аспирант, Федеральное государственное бюджетное образовательное учреждение высшего образования «Севастопольский государственный университет»,
ТКАЧЕНКО К.С., инженер 1-й кат., аспирант, Федеральное государственное бюджетное образовательное учреждение высшего образования «Севастопольский государственный университет», 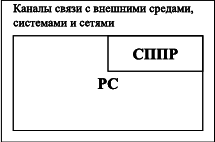
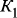 ,
, 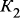 , …,
, …, 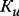 , …,
, …, 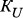 – каналы связи с внешними средами, системами и сетями;
– каналы связи с внешними средами, системами и сетями; ,
, 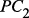 , …,
, …, 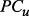 , …,
, …, 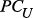 – информационно и функционально независимые структурные подразделения РС;
– информационно и функционально независимые структурные подразделения РС;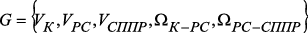 (1)
(1)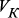 – множество вершин, соответствующих
– множество вершин, соответствующих 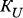 ;
;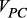 – множество вершин, соответствующих
– множество вершин, соответствующих 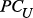 ;
;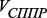 – множество вершин, соответствующих СППР;
– множество вершин, соответствующих СППР;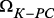 :
: 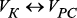 – множество ребер, связывающих
– множество ребер, связывающих 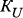 и
и 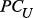 ;
;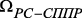 :
: 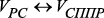 – множество ребер, связывающих
– множество ребер, связывающих 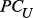 и СППР.
и СППР.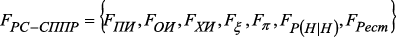 (2)
(2)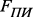 – функция получения и передачи информации;
– функция получения и передачи информации;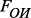 – функция обработки информации;
– функция обработки информации;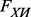 – функция хранения информации;
– функция хранения информации;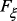 – функция оценки значений текущих потерь;
– функция оценки значений текущих потерь;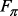 – функция обеспечения функционирования проекционных и беспроекторных методов и алгоритмов стохастической аппроксимации на основе автоматных рекуррентных последовательностей;
– функция обеспечения функционирования проекционных и беспроекторных методов и алгоритмов стохастической аппроксимации на основе автоматных рекуррентных последовательностей;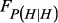 – функция оценки значений вероятностей гипотез о наличии ВА;
– функция оценки значений вероятностей гипотез о наличии ВА;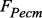 – функция формирования управляющих сигналов и выполнения динамической реструктуризации РС.
– функция формирования управляющих сигналов и выполнения динамической реструктуризации РС.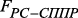 может быть представлено как
может быть представлено как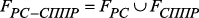 (3)
(3)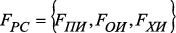 – подмножество функций, характерных для РС;
– подмножество функций, характерных для РС;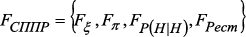 – подмножество функций, характерных для СППР.
– подмножество функций, характерных для СППР.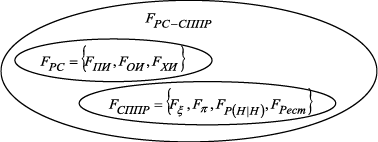
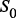
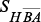
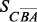
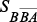
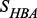
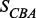
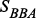
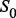 ,
, 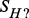 ,
, 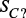 ,
, 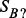 , где ? – символ-подстановка, определяются коммутированием ряда соединений из
, где ? – символ-подстановка, определяются коммутированием ряда соединений из 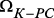 ,
, 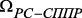 . Используемая для этих целей последовательность управляющих сигналов в значительной мере связана с конструктивными особенностями реальной РС и в настоящей работе не рассматривается.
. Используемая для этих целей последовательность управляющих сигналов в значительной мере связана с конструктивными особенностями реальной РС и в настоящей работе не рассматривается.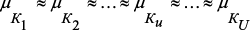
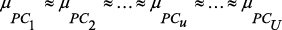 ,
, 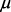 – производительность, управляющие сигналы могут быть такими:
– производительность, управляющие сигналы могут быть такими: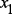 – отключены все связи из
– отключены все связи из 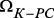 ;
;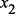 – подключена одна связь с наименьшим индексом из
– подключена одна связь с наименьшим индексом из 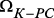 ;
;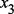 – подключены две связи с наименьшими индексами из
– подключены две связи с наименьшими индексами из 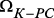 и так далее;
и так далее;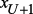 – подключены все связи из
– подключены все связи из 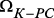 ;
;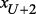 – подключена одна связь с наименьшим индексом плюс единица из
– подключена одна связь с наименьшим индексом плюс единица из 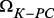 и так далее до
и так далее до 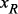 , где
, где 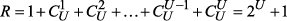 .
.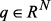 вектор-столбец
вектор-столбец 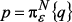 , принадлежащий
, принадлежащий 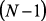 -мерному единичному
-мерному единичному  -симплексу
-симплексу 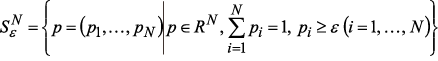 , определяется условием
, определяется условием 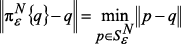 .
. 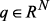 вектор
вектор 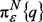 существует и единственен и
существует и единственен и 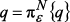 тогда и только тогда, когда
тогда и только тогда, когда 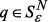 . В этом случае
. В этом случае 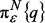 – оператор проектирования вектора
– оператор проектирования вектора 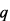 на
на  -симплекс.
-симплекс. 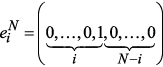 ;
; 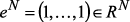 ;
;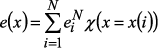 , если
, если 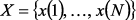 ;
; 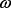 – элементарный исход.
– элементарный исход.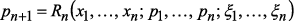 ,
, 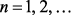 , где
, где 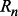 – вектор-функция движения со значениями в симплексе
– вектор-функция движения со значениями в симплексе 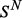 ,
, 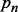 – вектор условных вероятностей выбора вариантов
– вектор условных вероятностей выбора вариантов 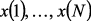 в момент времени
в момент времени 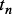 . Перед выбором очередного варианта
. Перед выбором очередного варианта 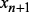 происходит расчет непосредственно следующих значений вероятностей выбора вариантов
происходит расчет непосредственно следующих значений вероятностей выбора вариантов 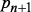 . Выбор варианта осуществляется методом деления отрезка: если известно значение
. Выбор варианта осуществляется методом деления отрезка: если известно значение 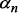 , полученное с выхода генератора псевдослучайной последовательности (закон распределения случайных величин равномерный) в момент времени
, полученное с выхода генератора псевдослучайной последовательности (закон распределения случайных величин равномерный) в момент времени 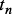 , то
, то 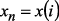 , причем номер
, причем номер  определяется исходя из соотношения
определяется исходя из соотношения 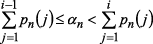 .
.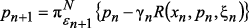 и по этой причине является проекционным.
и по этой причине является проекционным.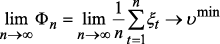 ,
, 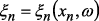 – случайные потери за выбор варианта
– случайные потери за выбор варианта 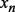 , произведенный в момент времени
, произведенный в момент времени 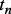 , и
, и 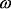 – элементарный исход.
– элементарный исход.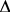 – параметром, влияющим на величину разницы между средним значением текущих потерь и ее предельным значением:
– параметром, влияющим на величину разницы между средним значением текущих потерь и ее предельным значением: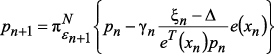 (4)
(4)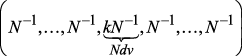 ,
, 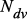 – номер доминирующего варианта,
– номер доминирующего варианта, 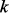 – масштабный множитель, выбираемый исходя из общесистемных соображений. Перед первым использованием элементы вектора корректируются оператором проектирования для обеспечения условия нормировки.
– масштабный множитель, выбираемый исходя из общесистемных соображений. Перед первым использованием элементы вектора корректируются оператором проектирования для обеспечения условия нормировки.