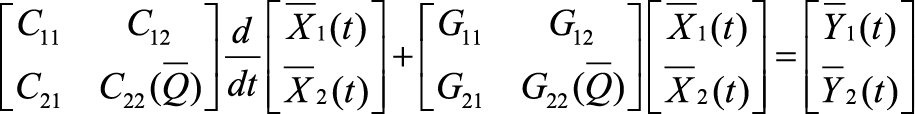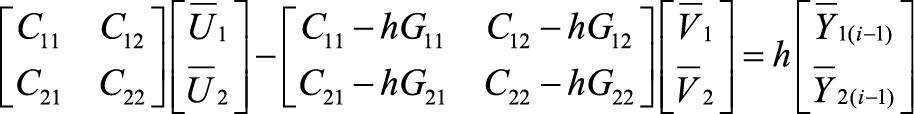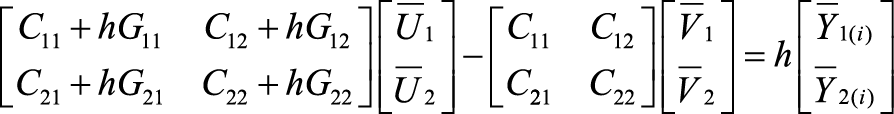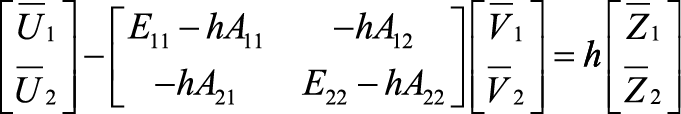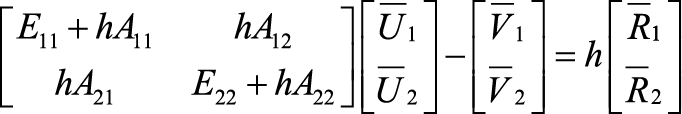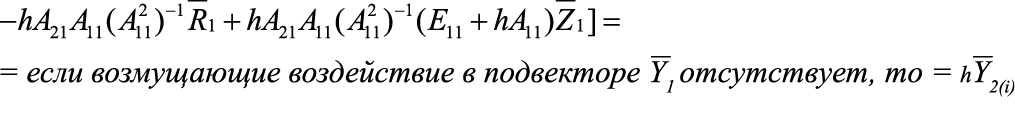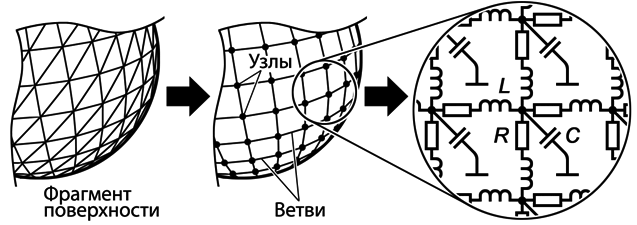
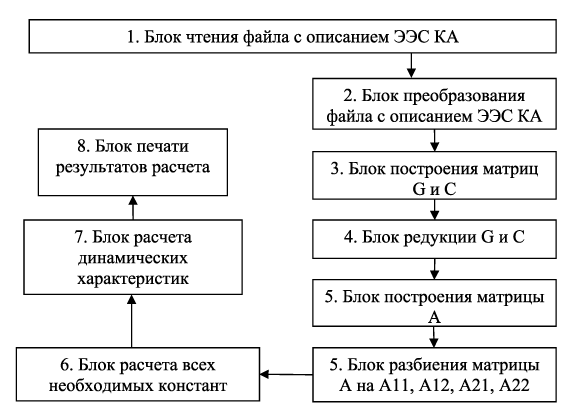
Разработка и анализ редуцированной вычислительной схемы

	ВОСТРИКОВ А.В., к.т.н., старший преподаватель НИУ ВШЭ, avostrikov@hse.ru		ЖАДОВ А.Д., студент 4-го курса НИУ ВШЭ
	БОРИСОВ Н.И., д.т.н., профессор НИУ ВШЭ		КЛЫШИНСКИЙ Э.С., к.т.н., доцент НИУ ВШЭ

Разработка и анализ редуцированной вычислительной схемы

В работе рассмотрен оригинальный подход к решению большой системы линейных обыкновенных дифференциальных уравнений первого порядка. В статье изложен вывод новой редуцированной вычислительной схемы на основе методов Эйлера. Приведены нюансы алгоритмизации построения вычислительной схемы. Оценена погрешность данной схемы по сравнению с неявным методом Эйлера. Посчитаны временные затраты на реализацию редуцированной вычислительной схемы. Исследование осуществлено в рамках Программы фундаментальных исследований НИУ ВШЭ в 2014 году

Одной из наиболее важных проблем длительной эксплуатации космических аппаратов (КА) являются электризация и связанные с этим процессом электростатические разряды (ЭСР). Отказы КА в 30% случаев происходят именно из-за электризации. Находясь в космическом пространстве, КА взаимодействует с разреженной плазмой. Заряженные частицы, накапливаясь на поверхности КА, создают разность потенциалов в десятки киловольт между элементами конструкции КА. Далее на поверхности КА возникают ЭСР, величина которых может достигать 100 А. Протекающие по поверхности КА токи вызывают в бортовой кабельной системе помехи в десятки вольт (В). Такие помехи способны вывести из строя бортовую радиоэлектронную аппаратуру [2]. Для сведения к минимуму возможных сбоев электроники КА необходимо смоделировать картину растекания тока по поверхности КА, провести расчет наводок в кабелях и дать рекомендации по оптимальному маршруту прокладки или их экранированию. С этой целью в МИЭМ были разработаны структурная электрофизическая модель (СЭМ) КА [3] и программное обеспечение (ПО) Satellite-MIEM для ее реализации. Метод СЭМ, опирающийся на идею методов искусственных аналогий [8], является самым эффективным для расчета переходных токов по корпусу КА.

Сначала необходимо смоделировать 3D-модель КА. Объемную полигональную модель КА можно построить в программе 3D MAX. ПО Satellite-MIEM преобразует 3D-модель в СЭМ КА (см. рис. 1). Полигональная модель состоит из совокупности прямоугольников или треугольников, преобразуемых в поверхностную равномерную сетку: совокупность связанных узлов. Количество узлов СЭМ крупногабаритного КА равняется (1…2)х105.

Рисунок 1. Преобразование полигональной модели КА в СЭМ

Каждую связь (ветвь) можно представить в виде RLC-цепи, образующей эквивалентную электрическую схему (ЭЭС) поверхности КА. ЭЭС содержит в себе резисторы, катушки индуктивностей, конденсаторы и источник тока. Процесс растекания токов по конструкции КА, содержащей вышеперечисленные схемные элементы, трактуется системой линейных обыкновенных дифференциальных уравнений (ОДУ). Уравнения, содержащие в себе R, L, C-элементы, описывают модель по переменному току (динамическая модель). При этом номиналы однотипных элементов равны, таким образом, математическая модель имеет три варьируемых параметра: R, L, C. По математической модели ЭЭС КА строят картину растекания токов, затем вычисляют наводки в кабелях. Для расчета переходных токов в ПО используется наиболее производительная программа расчета электрических схем LTSpice [3]. Итак, для построения картины растекания токов по поверхности КА нам необходимо решить систему ОДУ, причем количество уравнений равно числу узлов ЭЭС. Отметим также, что узлом с математической точки зрения является точка соединения двух радиотехнических элементов и соединение трех и более ветвей.

Построение картины растекания токов является наиболее трудоемким процессом во всей процедуре расчета наводок. Решение данной задачи в ПО LTSpice для схемы порядка 150 000 узлов требует около 83 часов на современных ПК [2], что неприемлемо для предприятий космической отрасли. Используемые в программах Spice неявные численные методы (метод трапеций, метод Гира и пр.) применимы только при расчете сравнительно небольших (до 10 000 узлов) моделей [3]. В связи с этим актуальной становится задача разработки новых ускоренных методов для решения больших систем линейных ОДУ.

Поэтому ставится задача разработки и анализа новой вычислительной схемы. Ранее в [4-6] был предложен подход, основанный на исключении из математической модели подвекторов с искомыми неизвестными (токи в ветвях или потенциалы в узлах), значения которых не превышают 1-2% от величины приложенного к месту разряда тока. Таким образом, из модели исключаются порядка 99% неизвестных, а расчет проводится в локальной области вокруг места разряда [5-7]. Однако полученная нами ранее редуцированная вычислительная схема имела заметную погрешность получаемых результатов.

Далее будет рассмотрен вывод новой редуцированной вычислительной схемы, опирающейся в большей степени на неявный метод Эйлера.

Постановка задачи

Модель схемы, сформированная в расширенном однородном координатном базисе (РОКБ), может быть записана в виде системы вот таких линейных обыкновенных дифференциальных уравнений [5]:

,

, (1)

где – – матрицы, при этом матрица содержит в себе номиналы индуктивных элементов и емкостных ЭЭС, а содержит номиналы проводимостей ЭЭС, – вектор варьируемых параметров модели, – вектор искомых фазовых переменных (напряжений во всех узлах схемы и токов, протекающих через индуктивные элементы), – вектор входных сигналов.

С учетом того, что , исходная задача (1) может быть записана в блочном виде:

,

, (2)

где - – матрицы, - – вектор, содержащий искомые выходные характеристики модели.

Необходимо преобразовать задачу (2) таким образом, чтобы итоговые выражения для вычисления выходных характеристик содержали в себе только вектор . Поскольку преобразованная задача будет состоять из m уравнений, при m << n произойдет значительное уменьшение трудоемкости вычислений динамических характеристик схемы, что будет доказано практическим примером. Также нужно будет вычислить погрешность результатов для оценки адекватности новой редуцированной схемы.

Разработка редуцированной вычислительной схемы

Для решения систем линейных обыкновенных дифференциальных уравнений на практике используются численные методы. Наиболее простыми являются явный и неявный методы Эйлера. Рассмотрим математические выражения, характеризующие эти методы, а затем на их основании выведем новую редуцированную вычислительную схему, в которой будем вычислять искомые m << n потенциалы в узлах ЭЭС.

Явный метод Эйлера задается выражением:

.

Неявный метод Эйлера определяется формулой:

.

Следовательно, для исходной системы уравнений (1) получим следующие выражения:

, (3) 

. (4)

Передвинув формулу явного метода (3) на один шаг назад и используя обозначение , запишем выражения (3), (4) в следующем виде:

, (5)

. (6)

В блочном виде система уравнений из двух методов будет выглядеть следующим образом:

, (7)

, (8)

в этоих выражениях векторы и обозначения векторов и соответственно.

В этом случае исходная система дифференциальных уравнений записана в явной форме и имеет простой вид:

, . (9)

В блочном виде явный и неявный методы Эйлера для такой системы записываются следующим образом:

,

,

где , , что эквивалентно системе их четырех подсистем уравнений:

, (10)

, (11)

, (12)

, (13)

Подставим из (10) в подсистему (12):

.

Таким образом, выражение для вектора имеет вид:

(14)

Теперь получим редуцированную формулу для вычисления подвектора решения. Она может быть получена не единственным образом в зависимости от того, какое из оставшихся условий (10) – (13) будет для этого использовано.

Далее подставим полученные значения и в выражение (13). В данном варианте будут использованы два условия из блочного неявного метода и одно из явного метода. Поскольку неявный метод обладает большей точностью, чем явный, итоговая редуцированная формула также должна быть более точной, чем полученная ранее в [5].

.

Подставим  из явного метода:

.

Подставим в полученное выражение  из (14):

.

Вычислим матрицу при векторе : 

. 

Пусть

Тогда имеем .

Вычислим матрицу при векторе :

.

Получим правую часть новой формулы: 

Если возмущающее воздействие в подвекторе , то рабочая формула из (13) с учетом ранее принятых обозначений имеет вид:

(15)

Программная реализация редуцированной вычислительной схемы

Для реализации редуцированной вычислительной схемы для расчета линейных ЭЭС большой размерности было разработано ПО (см. рис. 2), работу которого можно разбить на несколько этапов:

1. Конвертирование ЭЭС КА из программы LTSpice в модель, сформированную в РОКБ, для дальнейших преобразований.
2. Преобразование матриц для ускорения расчета по редуцированной вычислительной схеме.
3. Расчет ЭЭС с помощью вычислительной схемы.

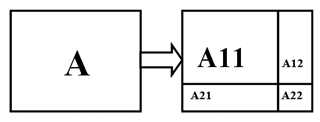
Рисунок 2. Иерархическая структура разработанного ПО

Для экономии машинной памяти на больших задачах все матрицы хранятся в списочном виде, то есть для больших разреженных систем, где количество нулевых элементов много больше, чем ненулевых, нет необходимости хранить нули. Такой подход увеличивает быстродействие программы.

Алгоритм конвертирования файла LTSpice в математическую модель (1), формируемую в РОКБ, для дальнейших преобразований был рассмотрен нами в [1].

Далее следует получить матрицу А из (9) путем умножения матрицы G на матрицу C^-1. Поскольку в матрице могут содержаться маленькие величины порядка 10^-12 (значения номиналов), а в матрице G – большие порядка 10³ , то при умножении матриц ЭВМ выдает некорректный результат. В этом случае необходимо масштабировать матрицу С таким образом, чтобы ненулевые коэффициенты матриц C и G имели одинаковый порядок. Приведем предложенный нами подход. Пусть необходимо решить систему линейных алгебраических уравнений (СЛАУ) вида:

, (16)

где ||C|| << ||G||, h > 0, h << 1, C = diag(c₁₁, ..., c_nn).

Добавим к матрице Ch матрицу Cq, такую, чтобы ||C(h + q)|| ≈||G||, т.е. получим СЛАУ вида:

(17)

Поскольку матрица СЛАУ (16) не совпадает с матрицей СЛАУ (17), вместо решения получим решение .

Раскроем скобки в СЛАУ (17):

Поскольку , получим СЛАУ:

,

где – вектор, все коэффициенты которого, кроме i-го, равны нулю, а i-й коэффициент равен единице.

С учетом того, что скалярные произведения имеют вид , имеем:

.

При замене переменных получим СЛАУ с n правыми частями, которую необходимо решить:

.

С учетом того, что , имеем: .

Итак, необходимо:

1) Решить СЛАУ 

(18)

2) Решить СЛАУ

  (19)

3) Решить СЛАУ

(20)

Далее из матриц С и G получаем матрицу А, которая разбивается на четыре блока – А₁₁(nxn), А₂₁(mxn), А₁₂(nxm) и А₂₂(mxm).

В [1] матрица А приводилась к треугольному виду с окаймлением с помощью метода определяющих величин, однако в ходе исследования было принято решение отказаться от этого подхода. Хотя в теории использование этого метода дает выигрыш в быстродействии при обращении матриц, этот способ приводит к потере некоторых специфичных свойств, таких как симметричность, что в дальнейшем влияет на конечное решение.

Поэтому далее математическая модель (2) ЭЭС строилась так: выбирались искомые узлы вокруг места разряда, которые затем включались в подвектор (см. формулу (2), в соответствии с перестановкой неизвестных в векторе был изменен порядок строк и столбцов в матрице А так, что в блоки А₂₁(mxn), А₁₂(nxm) и А₂₂(mxm) попадают искомые узлы (см. рис. 3).

Рисунок 3. Преобразование матрицы А

Таким образом, построение матрицы А сводится к следующим операциям:

1. Получение матрицы А путем перемножения соответсвующих матриц G и C^-1.
2. Поскольку матрица А имеет большое количество обусловленностей из-за большой разницы в порядках коэффициентов, то нами было принято решение масштабировать матрицу А по алгоритму Уилкинсона [9]. Если на диагонали матрицы А стоит элемент, меньший 1, то вся строка системы домножается до 1-го порядка.
3. Искомые узлы вокруг места разряда, заносим в подвектор . Искомые строки матрицы А поместить вниз, а столбцы вправо.
4. Если на диагонали есть нулевые элементы, то эту строку/столбец переставить вниз/вправо соответственно.
5. Получим блоки: А₁₁, А₁₂, А₂₁, А₂₂ (см. рис. 4).

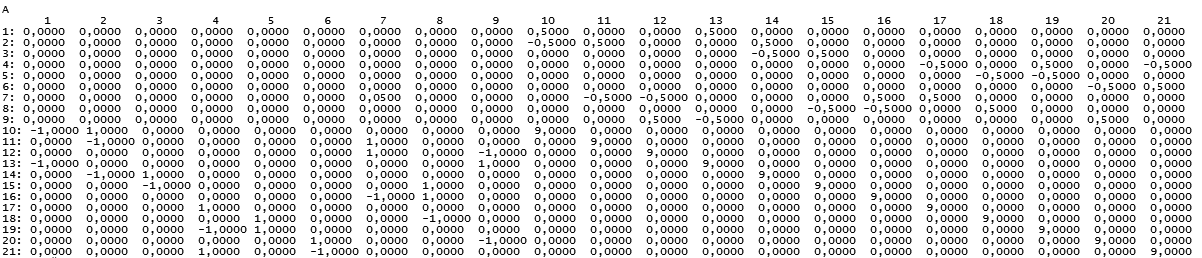
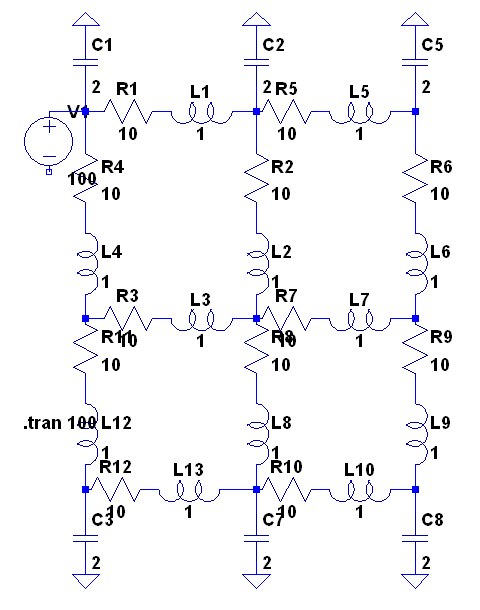
Рисунок 4. Результат преобразования матрицы

Далее вычисляются константы, полученные для (15):

Затем рассчитываются потенциалы в узлах по формуле (15):

Найденные из (15) коэффициенты сходятся к конечному решению, полученному из явного и/или неявного метода (3), (4). Для проверки адекватности результатов была вычислена локальная погрешность на каждом шаге по формуле:

Хотя ее величина меняется в зависимости от выбранного шага, в целом локальная погрешность интегрирования E << 1%. После того как был получен , строится картина растекания тока.

Расчет временных затрат

Практика показала, что расчет по вычислительной схеме больших математических моделей происходит на два-три порядка быстрее используемых в специализированном ПО методов. Время анализа ЭЭС, состоящей из 1000 узлов, разными методами при шаге h=0,001 с и количестве шагов 1000 приведено в таблице 1, а время построения редуцированной вычислительной схемы – в таблице 2.

Таблица 1. Время расчета ЭЭС различными методами

Численный метод	Время расчета (с)
Явный метод Эйлера	11,4
Неявный метод Эйлера	1057,01
Редуцированная вычислительная схема (3 узла в подвекторе )	0,063
Редуцированная вычислительная схема (11 узлов в подвекторе )	0,069
Редуцированная вычислительная схема (20 узлов в подвекторе )	0,073

Таблица 2. Время построения редуцированной вычислительной схемы, содержащей различное количество узлов в подвекторе 

Количество узлов в подвекторе	Время построения редуцированной вычислительной схемы (с)
Редуцированная вычислительная схема (3 узла в подвекторе )	851,4
Редуцированная вычислительная схема (11 узлов в подвекторе )	867,5
Редуцированная вычислительная схема (20 узлов в подвекторе )	885,1

Эксперименты осуществлялись на ПК с двухъядерным процессором (тактовая частота по 1,8 ГГц на каждом ядре) и ОЗУ 2 Гб. При этом результаты расчета по редуцированной вычислительной схеме отличаются от результатов неявного метода << 1%.

Практический пример

Вычислительная схема была протестирована на больших задачах, но проиллюстрировать данные примеры не представляется рациональным из-за большого объема данных. Для подтверждения результатов работоспособности редуцированной вычислительной схемы приведем примеры ЭЭС с небольшим количеством узлов (см. рис. 5).

Рисунок 5. ЭЭС, содержащая 21 узел

Оценим результаты, полученные после анализа схемы различными вычислительными схемами. Пусть к первому узлу подключен источник тока, а искомая локальная область – потенциалы в узлах: 1, 2, 4.

Результаты анализа, полученные неявным методом Эйлера и по редуцированной вычислительной схеме, отличаются на 0,0006% (см. рис. 6).

Рисунок 6. Расчет при h=0.001 с и количестве шагов = 1000

Локальная погрешность интегрирования на каждом шаге составляет E = 0,005% при величине шага h = 0,001с и E = 0,04% при h = 0,01с.

1. Жадов А. Д., Востриков А. В., Борисов Н. И., Тумковский С. Р. Программная реализация редуцированной вычислительной схемы численного интегрирования системы линейных дифференциальных уравнений на основе методов Эйлера. //«Системный администратор», №3, 2014 г. – С. 66-69 (http://samag.ru/archive/article/2647).
2. Л.С. Новиков, Г.В. Бабкин, Е.П. Морозов, С.А. Колосов, К.К. Крупников, В.Н. Милеев, В.С. Саенко. Комплексная методология определения параметров электростатической зарядки, электрических полей и пробоев на космических аппаратах в условиях их радиационной электризации. Руководство для конструкторов. – ЦНИИМАШ, Королев, 1995. – С. 160.
3. Востриков А. В., Абрамешин А. Е. Тестирование коммерческого программного обеспечения для моделирования и анализа эквивалентных электрических схем космических аппаратов. //«Технологии электромагнитной совместимости», №1, 2012 г. – С. 25-28.
4. Azmy S. Ackleh, Edward James Allen, R. Baker Kearfott, Padmanabhan Seshaiyer. //Classical and Modern Numerical Analysis: Theory, Methods and Practice/ 2009 by Chapman and Hall/CRC, 628 p.
5. Востриков А. В., Абрамешин А. Е., Борисов Н. И. Расчет наводок в бортовой кабельной сети космических аппаратов с помощью макромоделирования на основе методов Эйлера. //«Технологии электромагнитной совместимости», 2012. №1, 2012 г. – С. 19-24.
6. Востриков А. В., Абрамешин А. Е. Вычислительная схема ускоренного метода расчета наводок в бортовой кабельной сети космических аппаратов. //«Технологии электромагнитной совместимости», №3, 2012 г. – С. 22-28.
7. Востриков А. В., Борисов Н. И. Разработка эффективного метода анализа эквивалентных электрических схем космических аппаратов, использующего редукцию и разреженность матриц моделей. //В кн.: Новые информационные технологии в автоматизированных системах: материалы пятнадцатого научно-практического семинара./Отв. ред.: С. Р. Тумковский. – М.: Московский государственный институт электроники и математики, 2012. – С. 113-120.
8. Деньдобренко Б.Н., Малика А.С. Автоматизация конструирования РЭА. – М.: «Высшая школа», 1980. – С. 384.
9. Уилкинсон Дж. Алгебраическая проблема собственных значений. – ЧМ.: «Наука», 1970. – С. 564.

Ключевые слова: методы Эйлера, редуцированная вычислительная схема, преобразование матрицы, погрешность, алгоритм

Vostrikov A.V., Zhadov A.D., Borisov N.I., Klyshinsky E.S.

Development and analysis of the reduced computational schemes

Summary

The paper discusses a novel approach to solving large systems of linear ordinary differential equations of the first order. This paper describes the introduction of a new reduced computational scheme based on the Euler methods. Given the nuances of the algorithmic construction of the computational scheme. The estimated error of this scheme in comparison with the implicit Euler method. Calculated time implementation costs reduced computational schemes. The study was implemented in the framework of the Basic Research Program at the National Research University Higher School of Economics (HSE) in 2014.

Keywords: methods of Euler, reduced computational scheme, the transformation matrix, the error, the algorithm.

National Research University High School of Economics (NRU HSE)

Комментарии могут оставлять только зарегистрированные пользователи