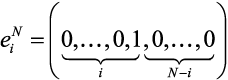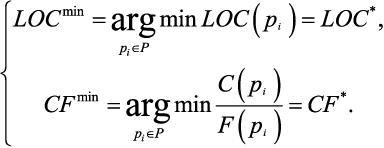|
|
|
|||||||||||||
|
|
Программные реализации оператора проектирования на эпсилон-симплекс Рассматривается несколько различных программных реализаций оператора проектирования на ε-симплекс. Приводятся необходимые формулы, таблицы В общем виде задача разработки и исследования программных реализаций оператора проектирования на ε-симплекс (πεN) актуальна и своевременна, при этом связана с важными научными и практическими задачами построения средств поддержки принятия решений (СППР), автоматизированных систем управления технологическими процессами (АСУ ТП), оптимизации и автоматизации производственных процессов, управления распределенными, облачными, вычислительными системами, сетями и средами, построения программных систем (ПС). В последних исследованиях и публикациях, в которых начинают решать данную проблему и на которые опирается автор [1-8], описывается решение различных задач с использованием проекционных и беспроекционных алгоритмов стохастической аппроксимации. При этом в работе [1] приводятся алгоритм и программная реализация на языке Фортран-IV оператора πεN. Нерешенной прежде частью общей проблемы, которой посвящена эта статья, является реализация оператора πεN на нескольких различных языках программирования высокого уровня (ЯП ВУ) с учетом разных подходов. Цель данной работы – разработка и исследование программных систем, реализующих оператор πεN. Известно [1], что рандомизированные стратегии, лежащие в основе стохастических автоматов, используют рекуррентные правила вида: pn+1 = Rn(x1,..., xn; p1,..., pn; ξ1,..., ξn), n = 1, 2,..., (1) В выраженни (1):
Когда происходит выбор очередного варианта xn+1, рассчитываются значения вероятностей выбора вариантов pn+1 по (1). Удобно выбор результирующего варианта осуществлять методом деления отрезка. Для удобства используются обозначения как в [1, 2], а именно: если X = {x(1),..., x(N)}; ω – элементарный исход. Пусть для любого q ∈ RN вектор-столбец p = πεN{q}, принадлежащий (N-1)-мерному единичному ε-симплексу: определяется условием: Для любого q ∈ RN вектор πεN{q} существует и единственен и q = πεN{q} тогда и только тогда, когда q ∈ SεN. Известны эффективные алгоритмы адаптивного выбора вариантов [1], которые можно подразделить на беспроекционные алгоритмы адаптивного выбора вариантов вида pn+1 = pn - γnR(xn, pn, ξn) и проекционные алгоритмы адаптивного выбора вариантов вида
Проекционные алгоритмы могут быть лучше беспроекционных, поскольку их можно использовать для решения более широкого класса задач (как с бинарными, так и с небинарными потерями ξn за счет обеспечения нормировки использованием оператора проектирования). При разработке СППР можно произвести сравнение различных реализаций оператора πεN на различных ЯП ВУ. Поскольку в основе СППР и моделей различных сетей и систем будут лежать методы и алгоритмы, использующие оператор πεN, то это сравнение позволит в дальнейшем производить выбор и обоснование используемых сред разработки и ЯП ВУ, в том числе и методом анализа иерархий (МАИ), и производить структурный синтез результирующих систем. Алгоритм выполняется следующей последовательностью шагов [1]: Шаг 0: k := 0, q0 := 0. Шаг i.1: Производится проецирование вектора qi-1 на SN-k. Шаг i.2: Если πN-k{qi-1} ∈ SN-k, то конец. Шаг i.3: Иначе исключаются из рассмотрения все отрицательные k компонентов, i := i + 1, qi := πN-k{qi-1}, переход к шагу i.1. Результаты разработки сводятся в таблицу 1. При этом в различных реализациях могут как использоваться, так и не использоваться возможности ЯП ВУ для абстракции списков (list comprehension, LC) – компактные описания операций обработки списков. Таблица 1. Разработанные программные системы, реализующие оператор πεN
Соответствующие фрагменты исходных кодов приводятся в листингах 1-7. Листинг 1. Исходный код P1 def defined(q): return [x for x in q if x is not None]
def sq1(q): return 1.0 - sum(defined(q))
def countOfDefined(q): return float(len(defined(q)))
def proek(q, eps): ar = 1.0 - eps * len(q) p = [((x - eps) / ar) for x in q] workIsDone = False while not workIsDone: workIsDone = True cod = countOfDefined(p) sq1p = sq1(p) p2 = [((x + (sq1p / cod)) if (x is not None) else None) for x in p] p = [(None if ((x is not None) and (x < 0.0)) else x) for x in p2] workIsDone = (p == p2) return [(eps + ar * (x if x is not None else 0.0)) for x in p]
if __name__ == '__main__': print(proek([1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1], 0.001))
Листинг 2. Исходный код P2 import math def defined(q): return [x for x in q if not math.isnan(x)]
def sq1(q): return 1.0 - math.fsum(defined(q))
def countOfDefined(q): return float(len(defined(q)))
def proek(q, eps): nan = float('nan') ar = 1.0 - eps * len(q) p = [((x - eps) / ar) for x in q] workIsDone = False while not workIsDone: cod = countOfDefined(p) sq1p = sq1(p) p2 = [(x + (sq1p / cod)) for x in p] p = [(nan if x < 0.0 else x) for x in p2] workIsDone = (p == p2) return [(eps + ar * (x if not math.isnan(x) else 0.0)) for x in p]
if __name__ == '__main__': print(proek([1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1], 0.001))
Листинг 3. Исходный код E1 -module(proek). -export([main/0, main/1, proek/2]).
main() -> main(args). main(_) -> run().
run() -> io:format("~p\n", [proek([1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1], 0.001)]).
proek(Q, Eps) -> AR = 1.0 - Eps * length(Q), P1 = lists:map(fun(X) -> (X - Eps) / AR end, Q), P2 = proekNaPolnySimplex(P1), lists:map(fun(X) -> Eps + AR * X end, P2).
proekNaPolnySimplex(Q) -> P1 = lists:map(fun(X) -> if X =/= nil -> X + sq1(Q) / countOfDefined(Q); true -> X end end, Q), P2 = lists:map(fun(X) -> if X < 0 -> nil; true -> X end end, P1), case countOfDefined(P1) =/= countOfDefined(P2) of true -> proekNaPolnySimplex(P2); false -> lists:map(fun(X) -> if X =/= nil -> X; true -> 0 end end, P2) end. sq1(Q) -> 1 - lists:sum(lists:filter(fun(X) -> (X =/= nil) end, Q)).
countOfDefined(Q) -> length(lists:filter(fun(X) -> (X =/= nil) end, Q)).
Листинг 4. Исходный код E2 -module(proek2). -export([main/0, main/1, proek/2]).
main() -> main(args). main(_) -> run().
run() -> io:format("~p\n", [proek([1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1], 0.001)]).
proek(Q, Eps) -> AR = 1.0 - Eps * length(Q), P1 = [(X - Eps) / AR || X <- Q], P2 = proekNaPolnySimplex(P1), [Eps + AR * X || X <- P2].
proekNaPolnySimplex(Q) -> P1 = [if X =/= nil -> X + sq1(Q) / countOfDefined(Q); true -> X end || X <- Q], P2 = [if X < 0 -> nil; true -> X end || X <- P1], case countOfDefined(P1) =/= countOfDefined(P2) of true -> proekNaPolnySimplex(P2); false -> [if X =/= nil -> X; true -> 0 end || X <- P2] end. defined(Q) -> [X || X <- Q, X =/= nil].%lists:filter(fun(X) -> (X =/= nil) end, Q). sq1(Q) -> 1 - lists:sum(defined(Q)). countOfDefined(Q) -> length(defined(Q)).
Листинг 5. Исходный код J1 public class Main {
public static double[] proekNazinPoznyak(double[] q, double e) { int N = q.length; // размерность вектора q double r = e * N; // εN double ar = 1.0 - r; // 1 - εN double ak = N; double sq1 = 0.0; // = 1 - ε{q_i}
double[] p = new double[N]; // результат boolean[] mon = new boolean[N]; boolean shagAlgo = true;
for (int i = 0; i < N; i++) { sq1 += q[i]; p[i] = q[i]; } sq1 = 1 - sq1;
for (int i = 0; i < N; i++) { mon[i] = false; p[i] = (p[i] - e) / ar; }
sq1 /= ar;
while (shagAlgo) { shagAlgo = false;
for (int i = 0; i < N; i++) { if (!mon[i]) { p[i] += sq1 / ak; } }
for (int i = 0; i < N; i++) { if (!mon[i] && (p[i] < 0.0)) { sq1 = p[i]; p[i] = 0.0; mon[i] = true; ak--; shagAlgo = true; break; } } }
for (int i = 0; i < N; i++) { p[i] = ar * p[i] + e; }
return p; } // proekNazinPoznyak
public static void main(String[] args) { double[] p = proekNazinPoznyak(new double[] { 1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1 }, 0.001); for (double x : p) System.out.println(" " + x); } }
Листинг 6. Исходный код J2 public class ProekWithLists {
private static double nil = Double.NaN;
private static boolean isNil(double x) { return Double.isNaN(x); }
public static double[] proekWithLists(double[] q, double eps) { boolean workIsDone; double[] p = new double[q.length]; double ar = 1.0 - eps * q.length; for (int i = 0; i < q.length; i++) { p[i] = (q[i] - eps) / ar; } do { workIsDone = true; double cod = countOfDefined(p); double sq1p = sq1(p); for (int i = 0; i < p.length; i++) { if (!isNil(p[i])) { p[i] += sq1p / cod; } } for (int i = 0; i < p.length; i++) { if (p[i] < 0.0) { p[i] = nil; workIsDone = false; } } } while (!workIsDone); for (int i = 0; i < p.length; i++) { if (isNil(p[i])) { p[i] = 0.0; } p[i] = eps + ar * p[i]; } return p; } private static double[] defined(double[] q) { java.util.ArrayList<Double> result = new java.util.ArrayList<Double>(); for (double y : q) { if (!isNil(y)) { result.add(y); } } double[] resultArr = new double[result.size()]; for (int i = 0; i < result.size(); i++) { resultArr[i] = result.get(i); } return resultArr; }
private static double sq1(double[] q) { double sum = 0; for (double y : defined(q)) { sum += y; } return 1 - sum; } private static int countOfDefined(double[] q) { return defined(q).length; } }
Листинг 7. Исходный код J2, продолжение public class Main { public static void main(String[] args) { double[] result = ProekWithLists.proekWithLists(new double[] { 1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1 }, 0.001); for (double x : result) { System.out.print(" " + x); } System.out.println(); } } Оценки метрических характеристик разработанных ПС, полученные с использованием программного обеспечения с открытым исходным кодом, сводятся в таблицу 2. Таблица 2. Полученные метрические характеристики разработанных ПС
В таблице используются обозначения:
Выбор подходящей системы производится следующим образом. Пусть P = {P1, P2, J1, J2, E1, E2,}. Тогда для оценки реализаций ПС по критериям LOC и C/F можно решить оптимизационную задачу: Для (3) искомым является piopt = P2. Вывод. В данной работе приведены результаты разработки и исследования программных систем, реализующих оператор πεN. Перспективой дальнейших изысканий по данной проблеме станут разработка и исследование оператора πεN на некоторых других ЯП ВУ и низкого уровня.
Ключевые слова: программные системы, оператор проектирования. Software implementations of the projection operator on the epsilon-simplex Tkachenko Kirill Stanislavovich, 1st cat. Engineer, graduate student, assistant, tkachenkokirillstanislavovich@mail.ru, tkachenkokirillstanislavovich@gmail.com Abstract There are a number of different software implementations of the projection operator on the ε-simplex in this article. The necessary formulas, tables are provided. Keywords: software systems, projection operator. |
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 ТКАЧЕНКО К.С., инженер 1-й кат., аспирант, ассистент,
ТКАЧЕНКО К.С., инженер 1-й кат., аспирант, ассистент,