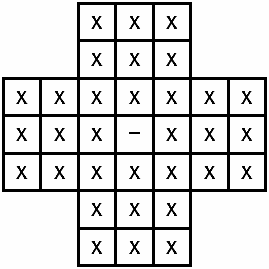
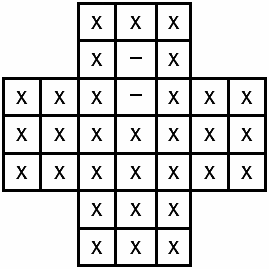
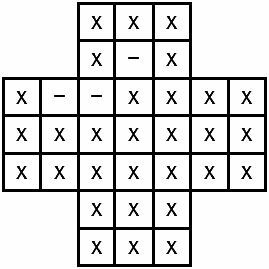
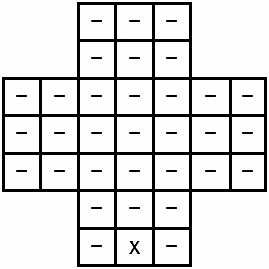
 |
|
|
|
Головоломка «Отшельник». Реализации решения «выигрывающих стратегий»
Головоломка «Отшельник» Существует определенный класс головоломок, который можно назвать «выигрывающие стратегии» [1] – их суть состоит в нахождении выигрышной стратегии. Широко известна головоломка «Отшельник» или «English peg solitaire» [2] с 32 колышками (фишками) Правила головоломки таковы: на крестообразном игровом поле (см. рис. 1) в начале игры находится 32 колышка (обозначенные символом «х») и одно свободное место (обозначенное символом «-»).
Рисунок 1. Начальное состояние игрового поля Все возможные ходы состоят в том, что колышек может «съесть» другой колышек, «перепрыгнув» через него на свободное место либо по горизонтали, либо по вертикали. Так, два последовательных хода из начальной позиции изображены на рис. 2, 3.
Рисунок 2. Состояние игрового поля после первого хода
Рисунок 3. Состояние игрового поля после второго хода При этом игра (решение головоломки) может заканчиваться, когда на доске остается один колышек (см. рис. 4).
Рисунок 4. Вероятное последнее состояние игрового поля Одной из существующих программных реализаций является [3] пример использования возможностей языка программирования Go. Укрупненный и упрощенный алгоритм функционирования [3] следующий:
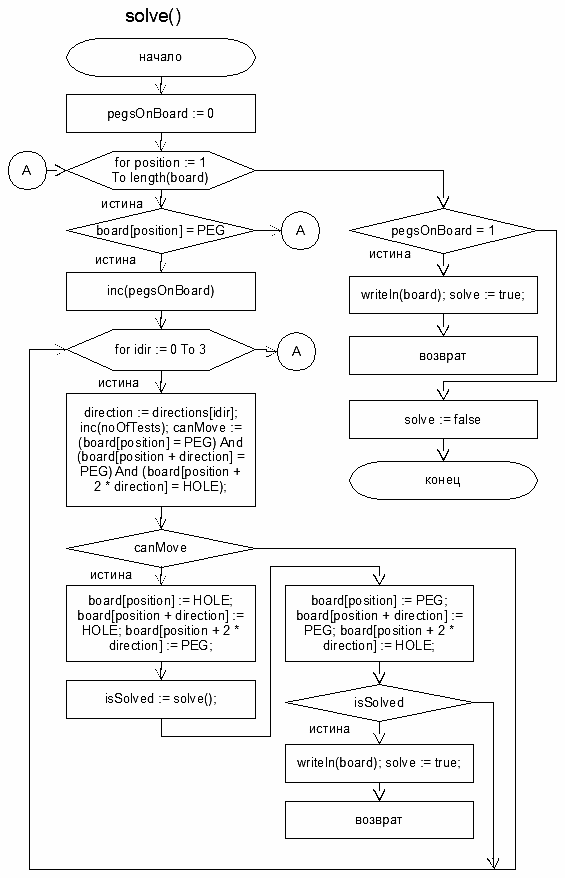
Далее будет рассматриваться модифицированный алгоритм, для которого схема основной рекурсивной функции выбора хода приводится на рис. 5. При этом используются паскале-подобные обозначения (некоторые отклонения от норм и требований к схемам алгоритмов обусловлены предельными значениями журнальной страницы). На рис. 5 и в нижеследующих листингах используются обозначения переменных (полей), сведенные в таблицу 1.
Рисунок 5. Алгоритм функционирования рекурсивной функции выбора хода Таблица 1. Переменные (поля)
Перед реализацией на нескольких языках программирования разумно проверить, в каком порядке нужно производить обход направлений при проверке возможности совершения игрового хода. Для этих целей разрабатывается программа, приведенная в листинге 1. В дальнейшем предполагается, что массив для представления игрового поля одномерный; направление задается разницей индексов целевого и рассматриваемого полей. Статью целиком читайте в журнале «Системный администратор», №10 за 2014 г. на страницах 82-85. PDF-версию данного номера можно приобрести в нашем магазине. |
КИРИЛЛ ТКАЧЕНКО, аспирант, Севастопольский национальный технический университет, 
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
