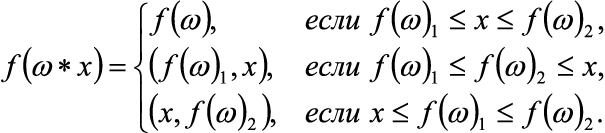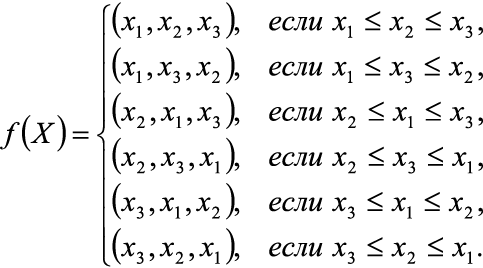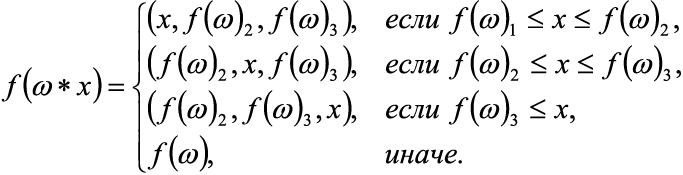 |
|
|
|
Особенности построения корректных программ с использованием метода вычисления индуктивных функций
Особенности построения корректных программ Рассматриваются возможности метода построения алгоритмов с использованием индуктивного вычисления функций на пространстве последовательностей применительно к последующей реализации на языке Java. Данная статья не является оригинальным исследованием; лучше истолковывать ее как краткое методическое указание, а автора, соответственно, составителем В настоящее время большое значение придается проверке корректности программного обеспечения (ПО), а также изначально верных алгоритмов проектирования и разработки. Для этих целей имеется значительное количество методов тестирования ПО и его формальной верификации. При этом в открытой печати, современных учебных пособиях, информационно-новостных сайтах, коллективных и личных блогах, посвященных информационным технологиям, программированию, информатике и вычислительной технике, относительно редко встречаются упоминания о методе вычисления индуктивных функций. Метод позволяет получать единственно возможные минимальные по потребляемой памяти однопроходные алгоритмы решения задач определенного класса. При этом программы, реализующие эти алгоритмы, могут иметь достаточно простую структуру, возможно решение при использовании потоковой обработки данных и в микропроцессорных системах. Данная публикация призвана заполнить существующий информационный пробел. В учебном пособии для вузов [1] содержится большое количество теоретического материала по данной тематике и некоторые примеры решения задач методом. Методический комплекс [2] содержит примеры использования метода на языке программирования Perl. При этом некоторые задачи на применение обозначенного метода, в том числе и из [1], не решены на кроссплатформенных, структурных, императивных языках программирования высокого уровня. Целью данной работы является подробное описательное решение некоторых задач средней сложности обозначенным методом с приведением готовых программ на языке Java без использования сторонних библиотек. Это позволит заинтересованным программистам начать использовать метод сразу, «по аналогии», в том числе и на других императивных языках программирования высокого уровня. Обозначения и краткие теоретические сведения Как и в [1], используются обозначения:
И, наконец, функция F : Q → Y называется индуктивной, если F(ω * x) можно вычислить, зная F(ω) и x. Для любой индуктивной функции на пространстве последовательностей существует минимальный по памяти однопроходный алгоритм. Чаще всего для некоторой последовательности Ω этот алгоритм будет выглядеть следующим образом: f1 := F(x1), x1 ∈ Ω; for each xi ∈ Ω, i ∈ 2,|Ω| do f1 := F(fi-1, xi) Очевидно, что если функция является индуктивной, то на конечной последовательности возможно реализовать ее вычисление. При этом программа будет корректной с точностью до мутаций исходного кода. В качестве примеров излагается решение двух задач из [1] с последующей реализацией на языке Java. Задача 1. Найти минимальное и максимальное значения последовательности Формализация задачи: f = «минимальное и максимальное значения», f : Ω1(R) → M ∈ R2, M = {(x1, x2)|x1 ≤ x2}. Аналитическое решение: Пусть здесь и далее f (ω)i – значение i-ой компоненты результата. При этом хранение f (ω)i возможно реализовать и без массива и/или иной структуры данных, в виде совокупности переменных. Начальная инициализация:
Основной цикл:
Программа, выполняющая вычисления по формулам (1)-(2), приводится в листинге 1. Первую строку условий в (2) можно не реализовывать. Для удобства демонстрации и отладки входная последовательность представлена в виде массива внутри кода, вывод осуществляется на стандартное устройство вывода. Значения массива получены с использованием генератора псевдослучайной последовательности, нормальное распределение, µ = 10,0; σ2 = 5,0. Переменные обозначаются латинскими буквами, при этом греческим буквам поставлены в соответствие латинские по первой букве произношения. Это касается и обозначенных в формулах функций на пространстве последовательностей. Листинг 1. Программа решения задачи 1 public class Main { public static void main(String[] args) { double[] o = { 8.1580e+0, 8.5010e+0, 1.7370e+1, 7.7220e+0, 1.3190e+1, 9.0350e+0, 1.1660e+1, 1.0920e+1, 6.4290e+0, 1.4050e+1, 1.3000e+1, 4.8380e+0, 9.8400e+0, 1.9450e+1, 9.8130e+0, 1.0770e+1, 5.2450e+0, 7.9320e+0, 1.0850e+1, 1.1060e+1, 8.8590e+0, 1.6640e+1, 1.7500e+0, 1.5080e+0, 2.1370e+1, 8.9400e+0, 8.8250e+0, 1.0410e+1, 7.6320e+0, 2.3720e+0, 1.2780e+1, 1.3780e+1, -1.1430e+0, 1.0470e+1, 8.7490e+0, 7.5710e+0, 1.7070e+1, 6.7480e+0, 1.0260e+1, 7.5710e+0, 8.6910e+0, 1.7790e+1, 1.4550e+1, 8.7880e+0, 1.7080e+1, 6.8140e+0, 8.1570e+0, 7.2240e+0, 9.9540e+0, -5.6870e-1 }; double fo1, fo2; if (o[0] <= o[1]) { fo1 = o[0]; fo2 = o[1]; } else { fo1 = o[1]; fo2 = o[0]; } for (int i = 2; i < o.length; i++) { double x = o[i]; if (fo1 <= fo2 && fo2 <= x) { fo2 = x; } else if (x <= fo1 && fo1 <= fo2) { fo1 = x; } } System.out.println(String.format("%.4f\t%.4f", fo1, fo2)); } } Результат выполнения программы из листинга 1: -1,1430 21,3700 Задача 2. Найти три наибольших значения последовательности Формализация задачи: f = «минимальное и максимальное значения», f : Ω1(R) → M ∈ R2, M = {(x1, x2)|x1 ≤ x2}. Аналитическое решение: Пусть здесь и далее f (ω)i – значение i-ой компоненты результата. При этом хранение f (ω)i возможно реализовать и без массива и/или иной структуры данных, в виде совокупности переменных. Начальная инициализация:
Основной цикл:
Вычисления по (3) можно реализовать и иным способом, более эффективно. Программа, выполняющая вычисления по формулам (3)-(4), приводится в листинге 2. Последнюю строку условий в (4) можно не реализовывать. Организация входных и выходных значений – как и в программе из листинга 1. Листинг 2. Программа решения задачи 2 public class Main { public static void main(String[] args) { double[] o = { 8.1580e+0, 8.5010e+0, 1.7370e+1, 7.7220e+0, 1.3190e+1, 9.0350e+0, 1.1660e+1, 1.0920e+1, 6.4290e+0, 1.4050e+1, 1.3000e+1, 4.8380e+0, 9.8400e+0, 1.9450e+1, 9.8130e+0, 1.0770e+1, 5.2450e+0, 7.9320e+0, 1.0850e+1, 1.1060e+1, 8.8590e+0, 1.6640e+1, 1.7500e+0, 1.5080e+0, 2.1370e+1, 8.9400e+0, 8.8250e+0, 1.0410e+1, 7.6320e+0, 2.3720e+0, 1.2780e+1, 1.3780e+1, -1.1430e+0, 1.0470e+1, 8.7490e+0, 7.5710e+0, 1.7070e+1, 6.7480e+0, 1.0260e+1, 7.5710e+0, 8.6910e+0, 1.7790e+1, 1.4550e+1, 8.7880e+0, 1.7080e+1, 6.8140e+0, 8.1570e+0, 7.2240e+0, 9.9540e+0, -5.6870e-1 }; double fo1, fo2, fo3; if (o[0] <= o[1] && o[1] <= o[2]) { fo1 = o[0]; fo2 = o[1]; fo3 = o[2]; } else if (o[0] <= o[2] && o[2] <= o[1]) { fo1 = o[0]; fo2 = o[2]; fo3 = o[1]; } else if (o[1] <= o[0] && o[0] <= o[2]) { fo1 = o[1]; fo2 = o[0]; fo3 = o[2]; } else if (o[1] <= o[2] && o[2] <= o[0]) { fo1 = o[1]; fo2 = o[2]; fo3 = o[0]; } else if (o[2] <= o[0] && o[0] <= o[1]) { fo1 = o[2]; fo2 = o[0]; fo3 = o[1]; } else { fo1 = o[2]; fo2 = o[1]; fo3 = o[0]; } for (int i = 3; i < o.length; i++) { double x = o[i]; if (fo1 <= x && x <= fo2) { fo1 = x; } else if (fo2 <= x && x <= fo3) { fo1 = fo2; fo2 = x; } else if (fo3 <= x) { fo1 = fo2; fo2 = fo3; fo3 = x; } } System.out.println(String.format("%.4f\t%.4f\t%.4f", fo1, fo2, fo3)); } } Результат выполнения программы из листинга 2: 17,7900 19,4500 21,3700 Видно, что решения задач 1, 2 однопроходные, потребляют сравнительно мало памяти, не требуют организации сортировки и вызова каких-либо библиотечных методов. Читатели могут самостоятельно решить эти две задачи, не используя вычисление индуктивных функций и стандартные библиотеки применяемых языков, и убедиться в громоздкости и сложности получаемых решений. Кроме того, в качестве «домашнего задания» можно предложить реализовать сравнения в программе из листинга 2 более экономно. В данной публикации рассмотрено решение некоторых задач, которые могут возникнуть в практической деятельности инженеров-программистов и системотехников. Перспективой дальнейших работ в этом направлении может стать приведение решений задач повышенной сложности.
Ключевые слова: индуктивные функции, обработка последовательностей, языки высокого уровня. Features for correct programs development with the using of the inductive functions calculations method К.S. Tkachenko, 1st cat. Engineer, graduate student, Sevastopol National Technical University, tkachenkokirillstanislavovich@mail.ru Annotation. This article describes the possibilities of the method of constructing algorithms using inductive functions computing on the space of sequences applied to the subsequent implementation in Java. This article is not original research; better interpret it as short guideline, and the author, accodingly, as the compiler. Кеуwords: inductive functions; processing of sequences; high-level languages. |
ТКАЧЕНКО К. С., инженер 1-й категории, аспирант, Севастопольский национальный технический университет, 
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
