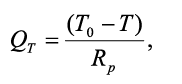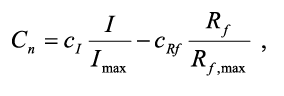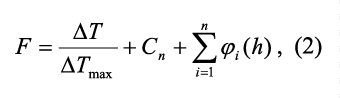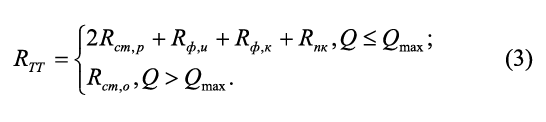|
|
|
|||||||||||||
|
|
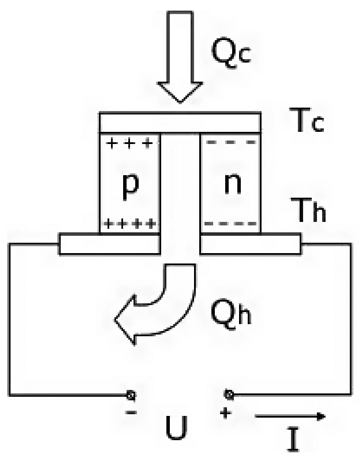
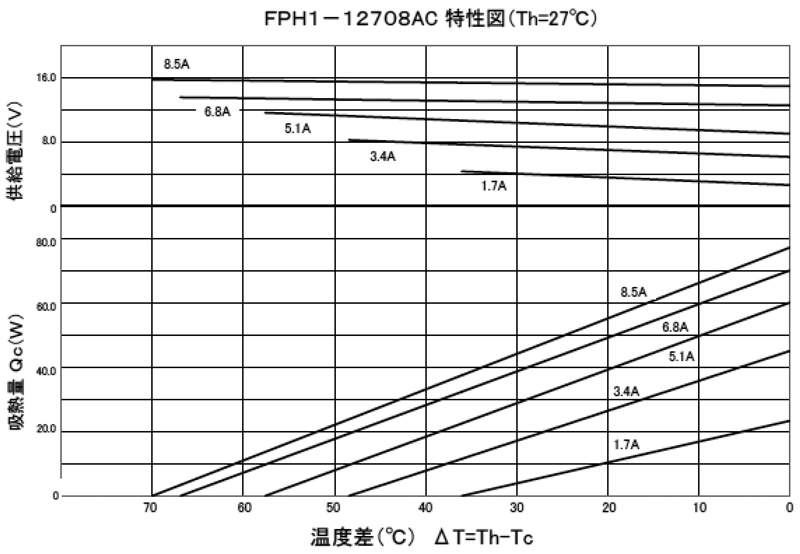
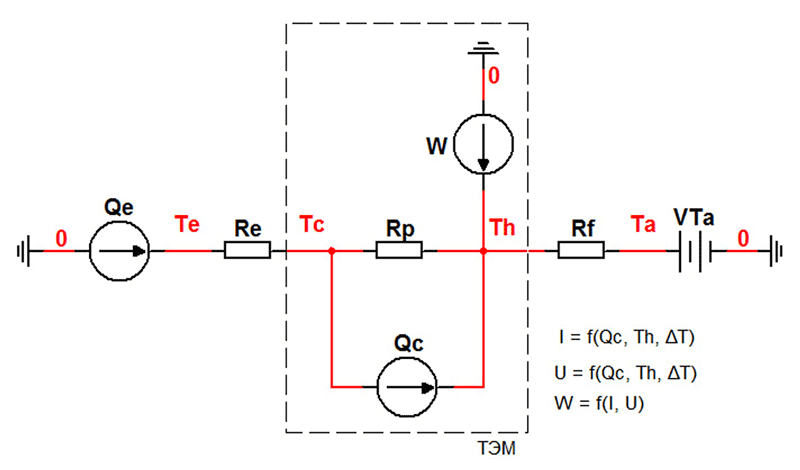
Оптимизационные модели В статье рассматривается оптимизационное моделирование термоэлемента Пельтье и тепловой трубы для повышения надежности современной бортовой и переносной радиоэлектронной аппаратуры с использованием современных информационных технологий в целях создания инновационной системы автоматизированного проектирования средств обеспечения ее тепловых режимов В современной бортовой РЭА (радиоэлектронной аппаратуре) для выполнения задач поддержания температурного режима входящих в него электрорадиоэлементов (ЭРИ) и блока в целом все чаще используются термоэлектрические модули (ТЭМ) Пельтье и тепловые трубы (ТТ), что обусловлено применением большого количества полупроводниковых микросхем, микропроцессоров и микросборок, функционирование которых с заданной надежностью неприемлемо вне определенного диапазона температур. Эта задача также актуальна для переносной РЭА, использующейся в сухопутных войсках, где требуется поддерживать тепловые режимы различных мобильных блоков питания и критичных к колебанию температур цифровых матриц тепловизоров. Помимо этого, ТЭМ и ТТ позволяют существенно снизить массу и габариты блоков РЭА, т.к. могут сократить количество и массу других средств – радиаторов, вентиляторов, кондуктивных теплоотводов. Ключевым преимуществом ТЭМ является возможность поддержания температуры охлаждаемого РЭА ниже температуры окружающей атмосферы внутри блока с прецизионным регулированием, а ТТ – формирование кондуктивной ветви с очень высокой тепловой проводимостью от охлаждаемого элемента к основной зоне отвода тепла. Необходимо заметить, что в настоящее время наблюдается тенденция в развитии программного обеспеспечения (ПО) инженерных расчетов, позволяющих с хорошей степенью точности уже на этапах предварительного проектирования производить оценку теплового режима блока РЭА без использования «тяжелых» и дорогостоящих систем, таких как ANSYS и Nastran (NX Thermal). Подобное ПО позволяет существенно сэкономить время на последующих этапах, т.к. помогает определиться с правильным выбором направления проектирования и использованием тех или иных средств обеспечения тепловых режимов. Требуется, чтобы выбранное решение было наиболее оптимальным с точки зрения затрат на реализацию и стоимости применения тех или иных средств обеспечения тепловых режимов. Учитывая, что существующие тепловые модели ТЭМ и ТТ не удобны для параметрической оптимизации, актуальной является задача создания удобных оптимизационных моделей с минимальным количеством факторов. В данной работе предлагаются оптимизационные модели ТЭМ и ТТ, выполненные в концепции электротепловой аналогии и состоящие из общепринятых элементов с небольшим количеством параметров. Оценка затрат на реализацию выполняется с помощью функции стоимости в качестве оценочного критерия эффективности и затратности решения оптимизационной задачи. Оптимизационная модель ТЭМ Оптимизационная модель ТЭМ необходима для нахождения наиболее оптимальных тепловых параметров ТЭМ, таких как холодопроизводительность Qc и тепловыделение Qh ТЭМ, при которых с минимальными затратами обеспечивается температура охлаждаемого объекта в заданных пределах с учетом термосопротивления Rf теплоотвода с самого ТЭМ в окружающую среду блока РЭА с температурой Ta. При этом эксплуатация ТЭМ при определенных значениях тепловых параметров в получаемом температурном поле приводит к затратам электрической мощности по току I при заданном напряжении U. Поэтому в оптимизационной модели необходимо оценивать как изменение тепловых параметров, так и затраты по току I, что реализуется с помощью экспертно-экономического показателя – стоимости реализации проектного решения с ТЭМ. Рассмотрим основные свойства ТЭМ. ТЭМ основан на эффекте выделения или поглощения тепла на границе двух разных проводников при прохождении через них электрического тока (см. рис. 1) [3]. Конструктивно ТЭМ состоит из набора полупроводниковых стержней p и n типа проводимости, соединенных металлическим мостиком (спай). При прохождении электрического тока I при напряжении U в охлаждающем спае поглощается тепло при температуре Tс и выделяется в другом спае при температуре Th. Рисунок 1. Схема действия элемента Пельтье Поглощаемая Qc и выделяемая тепловая Qh мощности выражаются через: Qc = α·I·∆T, Qh = Qc + W, где α = α1 + α2 – сумма термо-ЭДС обоих ветвей полупроводников, W – тепловая мощность, выделяемая внутри ТЭМ согласно эффекту Джоуля: W = U·R, ∆T = Th – Tc, R – электрическое сопротивление обоих ветвей. Мощность, затрачиваемая на теплопроводность между теплой стороной модуля и холодной, определяется через: где Rp – коэффициент теплового сопротивления модуля. Помимо этого, необходимо учитывать напряжение термо-ЭДС Eтэдс, возникающее при разности потенциалов между теплыми и холодными спаями согласно эффекту Зеебека в результате разности температур: Eтэдс = E·∆T, где E – коэффициент Зеебека. Эффект Томпсона принято оставлять без внимания ввиду малого его влияния по сравнению с другими эффектами. Существующие тепловые модели ТЭМ Пельтье основываются на приведенных зависимостях и конструктивных параметрах конкретного ТЭМ, например [1], и требуют подробного описания в модели всех происходящих в термопарах термоэлектрических явлений через параметры конструкции, например [2]. Это не всегда возможно осуществить в принципе ввиду того, что производитель, как правило, не публикует подробное описание конструкции своих модулей, размеров термопар, проводников и изоляторов, их свойств, применяемых материалов, а следовательно, неизвестны значения термо-ЭДС, α1, α2, параметры теплопроводностей и пр. В связи с вышеизложенным в данной работе предлагается тепловая модель ТЭМ, которая позволяет абстрагироваться от конструктивных параметров конкретных моделей термоэлементов и детального рассмотрения термоэлектрических явлений. Это возможно осуществить благодаря тому, что производитель (отечественный и зарубежный) публикует в листах спецификаций для конкретных моделей ТЭМ подробные функциональные зависимости Qc, I и U от температуры Th и разности температур ΔT на основе собственных экспериментально подтвержденных данных (см. рис. 2). Рисунок 2. Пример зависимостей параметров ТЭМ японского производителя На основе изложенного было проведено моделирование ТЭМ в соответствии с методом электротепловых аналогий и с использованием стандартных элементов программ симулирования электрических схем, поддерживающих анализ по постоянному току. Предлагаемая модель в дальнейшем может быть использована как самостоятельно для расчетов тепловых режимов ЭРИ и параметрической оптимизации ТЭМ, так и встроена в общую тепловую модель блока РЭА. На рис. 3 показана электрическая схема, моделирующая тепловые процессы ТЭМ и граничных тепловых объектов. В ней присутствует источник тепла Qe от охлаждаемого объекта, слой термопасты между ним и ТЭМ с тепловым сопротивлением Re и средство охлаждения горячей стороны ТЭМ с сопротивлением Rf, которое может быть радиатором, вентилятором, жидкостной системой, сборкой тепловых труб и т.п. Модель включает теплоотводящую ветвь холодопроизводительности Qc, тепловое сопротивление конструкции ТЭМ – Rp, ветвь выделения джоулевого тепла W на горячей стороне ТЭМ. Te, Tc, Th, Ta – температуры на объекте, холодной стороне, горячей стороне ТЭМ и окружающей среды соответственно, получаемые в результате расчета тепловой модели блока. Модель ТЭМ может быть встроена в общую модель теплообмена блока РЭА через узлы Tc, Th или Ta. Рисунок 3. Модель ТЭМ с охлаждаемым объектом Ток I, напряжение U и мощность W, необходимые для обеспечения заданной Qc, представлены функциональными зависимостями: I = b0 + b1Qc + b2∆T + b3Th + b11Qc2 + b22∆T2 + b33Th2, U = a0 + a1I + a2∆T + a3Th + a11I2 + a22∆T2 + a33Th2, W = I·U, где a0, a1, b0, b1… – коэффициенты полинома, определяемые в результате регрессионного анализа зависимостей Qc= f(I,Th,ΔT), U = f(I,Th,ΔT) по спецификации производителя (см. рис. 2) и определяются единожды для конструкции ТЭМ. Максимальные Qc, ΔT, Th ограничены для конкретной модели ТЭМ. Для определения коэффициентов регрессии использовался план эксперимента второго порядка, согласно которому регистрировалось восемь опытов полного факторного эксперимента по графикам зависимостей производителя, где каждый фактор варьировался не менее чем на трех уровнях. Полученные зависимости (1) позволили получить значения с точностью порядка (10-1÷10-2) от значений графиков производителя ТЭМ, которые, в свою очередь, основаны на многочисленных экспериментальных данных. Поэтому полученная точность является достаточной для проведения оптимизации. Исходными данными в процессе оптимизации на основе модели, включающей ТЭМ, является тепловыделение на охлаждаемом объекте Qe, диапазон температур, при которых обеспечивается его функционирование с требуемой надежностью Te ϵ [Tmin, Tmax], и температура окружающей среды, задаваемая VTa. Варьируемыми параметрами в процессе оптимизации являются Qc и Rf, через которые находятся параметры I, U, W согласно (1), что приводит к получению вектора температур Th, Tc, Te через решение системы уравнений по законам Кирхгофа для модели на рис. 3. Наиболее оптимальный режим работы ТЭМ с требуемой холодопроизводительностью Qc и минимальными затратами по току I, а следовательно, с минимальным тепловыделением W самого ТЭМ наблюдается при ΔT → 0 (см. рис. 2). Поэтому основной задачей в процессе оптимизации является поиск Qc и Rf, обеспечивающих такие значения температур Th и Tc,при которых ΔT будет минимальной и при этом будут обеспечиваться условия поддержания Te в заданных границах. Кроме того, необходимо оценивать затратность обеспечения питания самого ТЭМ и степень возможности реализации охлаждения его горячей стороны. Экспертно-стоимостную оценку эффективности решения с использованием ТЭМ, хорошо зарекомендовавшей себя в процессе практической оптимизации, можно представить в виде функции стоимости Сп от тока питания ТЭМ и средства его охлаждения: где I – ток обеспечения режима ТЭМ, Imax – максимально возможный ток для данной модели ТЭМ, сI – весовой коэффициент по току, Rf, Rf,max – расчетное и максимальное заданное тепловое сопротивление средства охлаждения ТЭМ, cRf – весовой коэффициент по выбранному средству охлаждения ТЭМ. Целевая функция, минимизируемая в процессе оптимизации, представляется зависимостью: где ΔTmax – максимальная заданная разность температур, φ – штрафные функции для недопущения выхода варьируемых параметров Qc, Rf и температуры охлаждаемого объекта Te за заданные границы. Оптимизация ТЭМ Оптимизацию ТЭМ предлагается производить в два этапа:
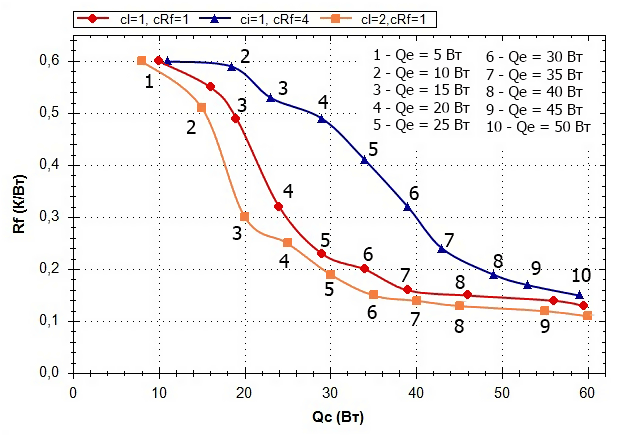
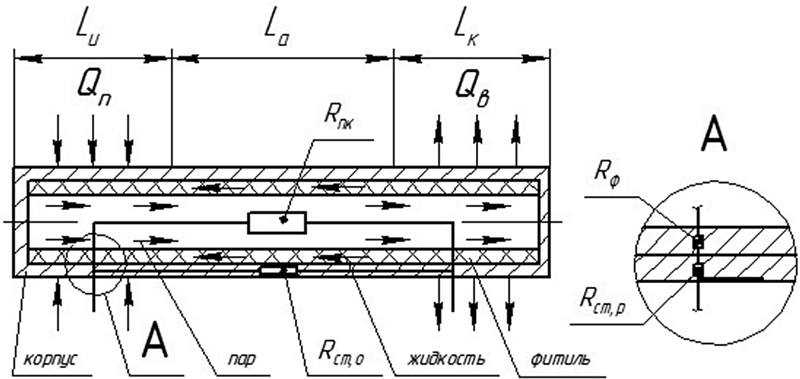
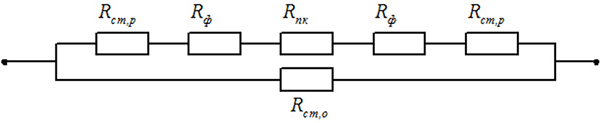
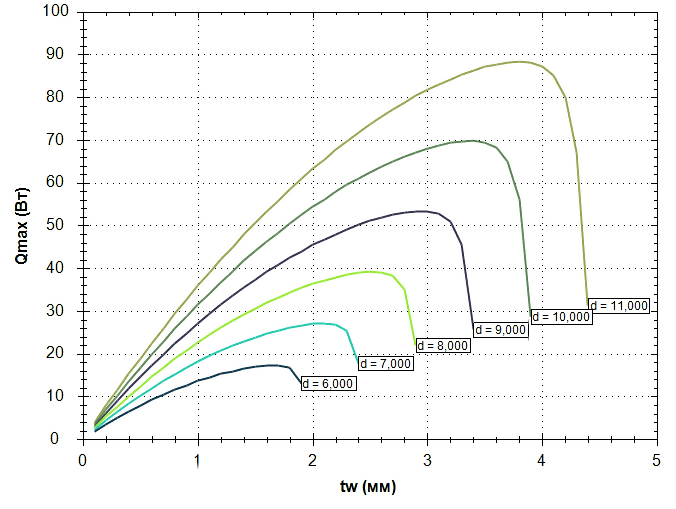
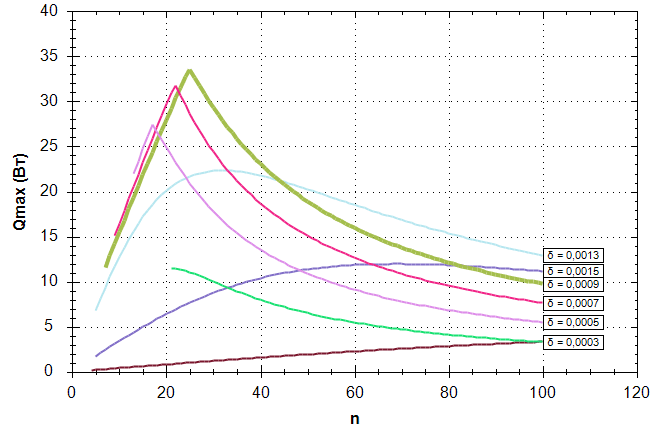
Важной особенностью ТЭМ является зависимость базовых параметров I, U и W (1) от температур Tc и Th. То есть, тепловой режим ТЭМ ключевым образом зависит от охлаждаемого объекта и охлаждения его самого. Так как в начале расчета Tc и Th неизвестны, то на предварительном этапе эти величины рассчитываются с допущением Th = Ta, ΔT = Th – p, где p – константа предварительной оценки разности температур, определяемая экспертом исходя из необходимости обеспечения требуемой температуры охлаждаемого объекта Te. На практике величина p обычно составляет 10-30°, что дает точность в разности ΔT на разных этапах расчета порядка (10-2)°. На рис. 4 представлены графики оптимальных параметров Qc и Rf (точки на графиках), полученные в результате оптимизации тепловой модели, включающей ТЭМ Криотерм ICE-71 при разных значениях тепловыделения охлаждаемого объекта Qe и различных весовых коэффициентах сI и сRf. Температура окружающей среды задана через VTa равной 35°C. Рисунок 4. Результат оптимизации ТЭМ Криотерм ICE-71 Оптимизационная модель ТТ Классические ТТ могут успешно применяться в конструкциях РЭА любого исполнения вследствие ряда преимуществ по сравнению с традиционными средствами охлаждения и термостатирования, т.к. не требуют обслуживания, электрической мощности, обладают малым тепловым сопротивлением и способны переносить значительное количество тепла. В настоящее время актуальной является задача оптимизации параметров ТТ для различных задач, что требует наличия подходящей тепловой модели ТТ с минимально необходимым набором параметров, которая будет адекватно соответствовать процессам, протекающим при теплообмене. Типичная ТТ общей длиной LТ с круглым поперечным сечением работает в режиме теплопереноса от зоны испарения длиной Lи, в зону конденсации длиной Lк. Длина транспортной или адиабатической зоны в общем случае равна Lа, в частном случае может быть равна нулю. Считаем, что тепловой поток в зонах испарения и конденсации распределен равномерно. Фитиль может быть выполнен из проволочной сетки, упакованных (спеченных) шаров или в форме канавок в корпусе трубы. Форма фитиля – цилиндрическая и имеет плотный контакт с корпусом ТТ, при этом тепловым сопротивлением между корпусом и фитиле можно пренебречь. Тепловое сопротивление проходящему тепловому потоку в осевом и радиальном направлении равно Rст,о и Rст,р соответственно. Rпк – тепловое сопротивление парового канала, Rф – тепловое сопротивление насыщенного жидкостью фитиля, Qп – поглощаемый тепловой поток от охлаждаемого объекта, Qв – тепловой поток, отдаваемый ТТ (см. рис. 5). Рисунок 5. Схема тепловой трубы с элементами тепловых сопротивлений Моделирование ТТ в соответствии с методом электротепловой аналогии можно произвести в виде набора связанных тепловых сопротивлений (см. рис. 6). Рисунок 6. Тепловая модель ТТ Суммарное тепловое сопротивление RТТ в таком случае находится через: где тепловые сопротивления R = f(q,T), Qmax = f(q,T), Т – рабочая температура, q – варьируемые при оптимизации параметры: D – внешний диаметр корпуса ТТ, tp – толщина стенки корпуса, ψ – угол наклона относительно гравитационного поля, δ, ω, n – глубина, ширина и количество канавок фитиля соответственно (параметры сеточного слоя для сеточного фитиля или параметры спеченных шариков), табличные значения свойств рабочей жидкости и материала корпуса при рабочей температуре Т, Q – тепловой поток от охлаждаемого объекта. Тепловые сопротивления из (3) в конечном виде могут быть получены по методике [3]. В ряде работ, например [2, 3], тепловое сопротивление вдоль оси ТТ не участвует в моделировании, т.к. при Q ≤ Qmax тепловое сопротивление в радиальном направлении и через паровой канал на несколько порядков меньше, чем в осевом. Данная тепловая модель учитывает случай выхода значения теплового потока Q охлаждаемого объекта за максимально возможный для данной ТТ Qmax, что на практике приводит, в частности, к «осушению фитиля» в зоне испарения от рабочей жидкости. В этом случае теплоперенос от зоны испарения к зоне конденсации производится только по корпусу ТТ. В процессе автоматизированного поиска оптимальных параметров ТТ значение функции (3) будет стремиться к максимуму для наиболее нежелательных значений параметров функций RТТ и наиболее существенно (на несколько порядков) возрастать при Q > Qmax. При этом значение Rст,о для упрощения расчета рекомендуется брать как некое большое число, обеспечивающее неприемлемое значение RТТ и исключающее выбор параметров ТТ, работающей за пределами Qmax. Разность температур в зоне испарения и конденсации на внешнем корпусе ТТ находится при встраивании кондуктивной ветви с тепловым сопротивлением RТТ в общую тепловую модель РЭА, где может быть также использована при проведении структурной или параметрической оптимизации системы обеспечения теплового режима блока РЭА в целом. Максимальная теплопередающая способность Qmax наиболее существенно лимитируется капиллярным ограничением передающей способности фитиля Qc,max и ограничением по кипению теплоносителя Qb,max. Данные ограничения могут быть получены экспериментально и затем представлены регрессионной зависимостью аналогично (1), данными производителя либо получены расчетным путем. Если не известно значение Qmax для оптимизационной модели из экспериментальных данных, то для различных ТТ c одним испарителем и одним конденсатором, имеющих постоянную площадь поперечного сечения корпуса, Qc,max и Qb,max могут быть найдены по методике [3]. В процессе оптимизации Qmax определяется как: Qmax = min(Qc,max, Qb,max). На рис. 7 представлена зависимость для Qmax, полученная в результате моделирования ТТ с медным корпусом, водой в качестве рабочей жидкости и различных значениях толщины скрученной сетки медной проволоки – фитиля и при разных диаметрах корпуса. Графики показывают ключевое влияние диаметра фитиля d и его толщины tw на составляющую капиллярного ограничения Qc,max, что подтверждается экспериментальными данными [4]. Справа и сверху Qc,max ограничивается пределом по кипению теплоносителя Qb,max. Задача нахождения оптимальных параметров ТТ требует оценки эффективности изменения каждого параметра, что может быть сделано с помощью экспертного показателя – стоимостной функции. В общем случае суммарная стоимость применения ТТ может быть представлена через стоимостные функции: СTT = λжNж(τ) + λкCк(ε) + λфCф(μ) (4) где Ск и Сф, – стоимостные функции для параметров конструкции ТТ и параметров фитиля, λж, λк, λф,– весовые коэффициенты важности, Nж – параметр теплопередающей способности теплоносителя [5], τ – варьируемый тип теплоносителя, ε – варьируемые конструктивные параметры ТТ, μ – варьируемые параметры фитиля. На параметры накладываются ограничения. Вид стоимостных функций и весовые коэффициенты задаются экспертом перед выполнением процесса оптимизации. На рис. 7 представлены значения Qmax, полученные в результате расчета параметров тепловой трубы с фитилем в форме прямоугольных канавок глубиной δ в алюминиевом корпусе диаметром 12 мм и аммиаком NH3 в качестве теплоносителя. Рисунок 7. Зависимость Qmax от диаметра d при разной толщине фитиля tw Максимумам соответствуют наиболее оптимальные значения параметров фитиля, при этом стоимостная функция (4) позволяет ввести ограничения в процесс оптимизации и выбрать наиболее эффективное решение с учетом затрат на реализацию ТТ с полученными параметрами. Рисунок 8. Пример зависимости Qmax от числа канавок n и глубины канавки δ (м) *** В результате данной работы предложены оптимизационные тепловые модели ТЭМ и ТТ с небольшим набором параметров. Данные модели могут быть использованы при самостоятельной параметрической оптимизации элементов, а также в составе блока РЭА при структурной и параметрической оптимизации, т.к. позволяют оценить целесообразность применения проектного решения для системы обеспечения температурного режима блока с помощью стоимостных функций. Тепловые модели могут быть использованы в любых программах, поддерживающих расчет по постоянному току, например, ngspice, Multisym, LTSpice и др. Полученные оптимизационные модели являются частью разрабатываемого программного обеспечения для структурного и параметрического синтеза систем обеспечения тепловых режимов блоков РЭА.
Ключевые слова: Радиоэлектронная аппаратура, автоматизация проектирования, тепловой режим, оптимизация, элемент Пельтье, тепловая труба. Optimization models thermocouple Peltier and heat pipes Gromov I.U, A. M. Kozhevnikov A.M. Annotation. The article considers the optimization modeling thermocouple Peltier and heat pipes to increase the reliability of modern on-Board and portable electronic equipment with use of modern information technologies to create innovative computer-aided design tools ensure its thermal regimes. Кеуwords: Radio-electronic equipment, design automation, thermal regime, optimization, Peltier element, heat pipe. |
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|