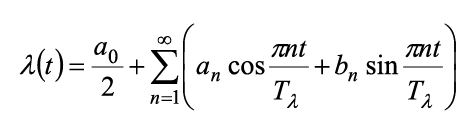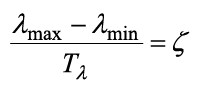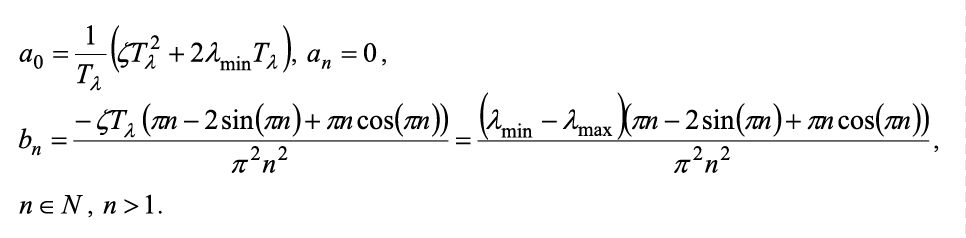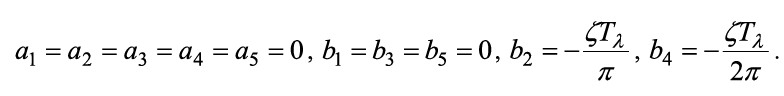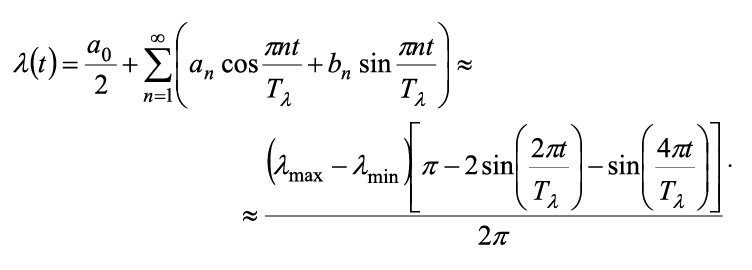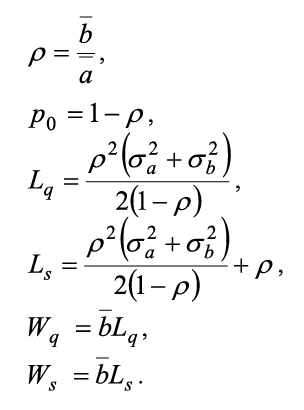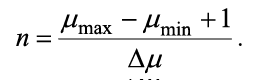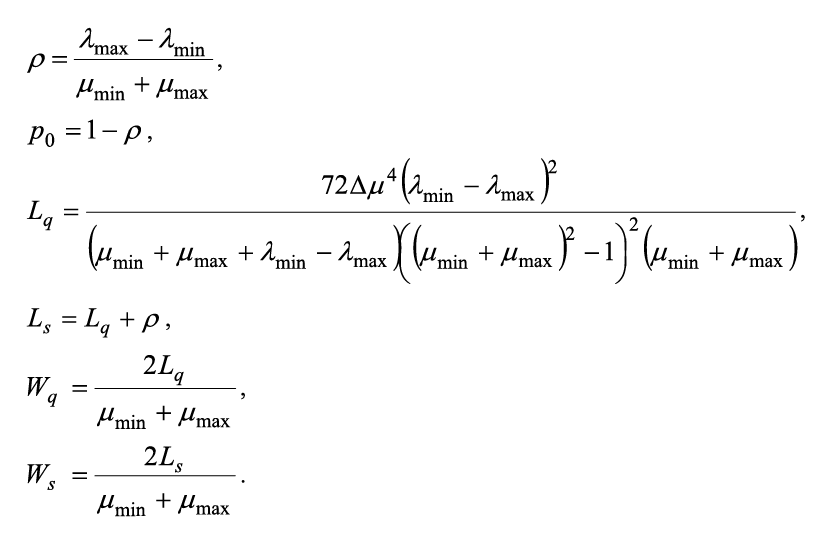 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Узел однородной вычислительной сети под воздействием вирусных атак как система G/G/1
Узел однородной вычислительной сети Предлагается и рассматривается аналитическая модель узла однородной вычислительной сети под воздействием вирусной атаки с позиций теории массового обслуживания как система G/G/1. Приводятся необходимые формулы, рисунки, таблицы В настоящее время, как никогда, своевременна и актуальна проблема обнаружения несанкционированных воздействий и вирусных атак (ВА). Эта проблема связана с важными научными и практическими задачами обеспечения безопасности, корректности функционирования, готовности, работы в реальном времени разнообразных компьютерных систем и комплексов, распределенных систем, сред и сетей, отдельных компьютеров. Существенную сложность представляет отсутствие разумного компромисса между затратами на частоту контроля и возможными потерями за счет ВА. Проверки, тестирование и возможное обнаружение ВА требуют затрат. Эти затраты тем выше, чем чаще будут проводиться контролирующие действия. Но, с другой стороны, при низкой частоте контроля повышаются вероятные потери за счет ВА и прочих вредоносных действий. Для предложения необходимых правил компромисса и решения возникающих оптимизационных задач необходимы разработка, исследование и использование системы поддержки принятия решений (СППР). Имеется ряд последних исследований и публикаций, в которых начаты решения данной проблемы и на которые опирается автор. В статье [1] рассматривается структурный синтез систем мониторинга и описывается СППР по выбору структуры системы мониторинга и дисциплины опроса узлов фрагмента компьютерной сети. В публикации [2] исследуются эффективность процедур безусловной оптимизации для параметрической идентификации трафика коммутационного узла сети. В работе [3] производится сравнение работы нестационарной двухфазовой системы в стационарном и нестационарном режимах, вводится коэффициент оценки влияния нестационарности на результаты моделирования. Подход, позволяющий с помощью введения версионно-модельной избыточности парировать дефекты проектирования и взаимодействия алгоритмических и вычислительных составляющих имитационных моделей и, таким образом, принимать эффективные решения, опублико-ван в [4]. Нерешенной прежде частью общей проблемы, которой посвящена данная статья, является аналитическое приближение системы массового обслуживания (СМО) G/G/1, пригодной для практических инженерных расчетов. Целью работы является разработка аналитической модели узла однородной вычислительной сети под воздействием ВА как СМО G/G/1. Для упрощения разработки аналитической модели считается, что ВА подвергается с априори неизвестной интенсивностью только один узел вычислительной одноранговой сети. При этом возрастает функциональная интенсивность входного потока заявок λ(t) (пакетов задач) для узла. Периодически происходит контроль за ВА, и при обнаружении ВА линейно возрастает производительность обработки заявок μ(t), которая линейно уменьшается в отсутствии предположений о ВА. Предположим, что интенсивность λ(t) входного финитного, ординарного, с отсутствием последствия потока полезных заявок и заявок с ВА имеет вид периодической кусочно-линейной функции, изображенной на рис. 1.
Рисунок 1. Периодическая кусочно-линейная функция интенсивности λ(t) На этом рисунке:
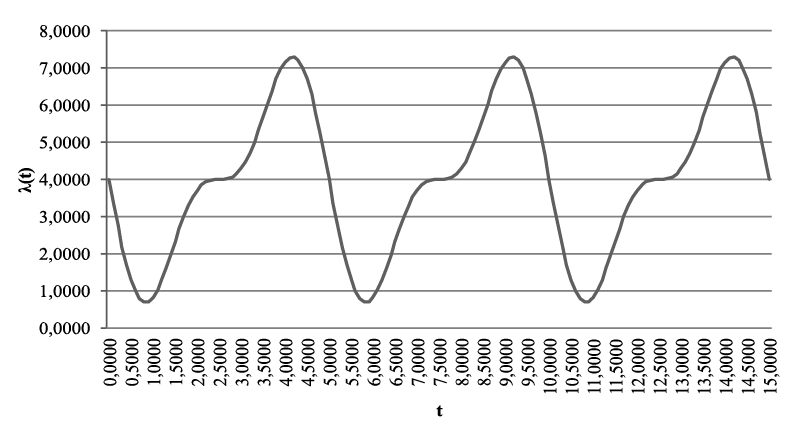
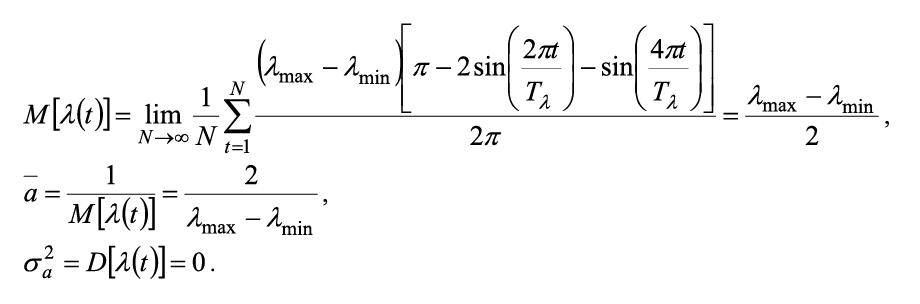
Для удобства выполнения расчетов функция λ(t) разлагается в ряд Фурье. Существующие справочники либо не дают ответа на вопрос о коэффициентах Фурье для данной функции, либо содержат не совсем верные формулы [5]. Разумно использовать подход, предложенный [6]. Искусственно продолжив λ(t), в отрицательные значения t можно записать ряд Фурье для функции λ(t) на отрезке [-Tλ; Tλ] с периодом T = 2Tλ в виде:
Обозначается: Тогда коэффициенты ряда рассчитываются по формулам:
При использовании САПР для математических вычислений, ограничившись пригодным для практических целей числом членов ряда, получается, что:
Для наших целей:
Откуда и из (1), (2):
И в итоге:
Пример графика приближения функции λ(t), рассчитанный по формуле (3) для λmin = 2,0; λmax = 10,0; Tλ = 5,0 приводится на рис. 2.
Рисунок 2. График приближения функции λ(t) Теперь, для получения приближения функции μ(t) в пригодном для аналитической модели виде, необходимо сформулировать правила функционирования балансировщика нагрузки узла. Пусть решение системой принимается в момент времени tn+1 > tn и ∆μ(t) – некоторый, наперед заданный и определенный в директивном порядке, шаг изменения производительности обработки узла, μmin, μmax – аналогичным образом определенные минимальное и максимальное значения μ(t) ∈ [μmin; μmax]. 1. Начальное значение μ(0):= μmin. 2. Если оценка средней длины очереди заявок в системе в момент времени tn+1 Lq(tn+1) больше, чем оценка средней длины очереди заявок в системе в момент времени tn Lq(tn), то есть Lq(tn+1) > Lq(tn), то тогда μ(tn+1):= min{μ(tn)+∆μ(t), μmax}. 3. Если оценка средней длины очереди заявок в системе в момент времени tn+1 Lq(tn+1) не превышает оценку средней длины очереди заявок в системе в момент времени tn Lq(tn), то есть Lq(tn+1) ≤ Lq(tn), то тогда μ(tn+1):= max{μ(tn)–∆μ(t), μmin} . Известно [7-10], что в одноканальной СМО с произвольным потоком заявок и произвольным распределением времени обслуживания затруднительно получить точные аналитические формулы, в том числе и для оценок средней длины очереди в системе. Но в работе [11] приводятся аналитические выражения для расчета G/G/1 при большой загрузке p≈1, а в книге [8] – грубая оценка средней длины очереди. Поскольку при ВА действительно p≈1 и на основании формул Литтла, соотношений из [7-11] получается:
В (4) и далее:
С помощью САПР можно получить:
При t → ∞ μ(t) – дискретная равномерная случайная величина с числом значений: Поэтому
На основании (4) – (6) получается аналитическая модель системы S(λmin, λmax, μmin, μmax, ∆μ), не зависящая от Tλ и удобная для инженерных расчетов:
Исходный код программной системы расчетов аналитической модели, написанной на языке программирования высокого уровня Java, приводится в листинге 1. Листинг 1. Исходный код программной системы расчетов аналитической модели public class AnalitModel { private static double sqr(double x) { return x * x; } private static String doubleToString(double x) { return String.format("%.4f", x); } public static void main(String[] args) { StringBuffer out = new StringBuffer(); double mu_min = 20.0, mu_max, delta_mu = 10.0; double lambda_min = 10.0, lambda_max; double rho = 0.9999, p0 = 1 - rho, lq, ls, wq, ws; int int_mu_max = 100;
// для исключения сравнений вещественных чисел
while (int_mu_max <= 180) { mu_max = int_mu_max; double mu_min_mu_max = mu_min + mu_max; lambda_max = rho * mu_min_mu_max + lambda_min; double lambda_min_lambda_max = lambda_min - lambda_max; lq = (72 * sqr(sqr(delta_mu)) * sqr(lambda_min_lambda_max)) / ((mu_min_mu_max + lambda_min - lambda_max) * sqr(sqr(mu_min_mu_max) - 1) * mu_min_mu_max); ls = lq + rho; wq = 2.0 * lq / mu_min_mu_max; ws = 2.0 * ls / mu_min_mu_max; out.append(doubleToString(lambda_min)).append('\n'); out.append(doubleToString(lambda_max)).append('\n'); out.append(doubleToString(mu_min)).append('\n'); out.append(doubleToString(mu_max)).append('\n'); out.append(doubleToString(delta_mu)).append('\n'); out.append(doubleToString(rho)).append('\n'); out.append(doubleToString(p0)).append('\n'); out.append(doubleToString(lq)).append('\n'); out.append(doubleToString(ls)).append('\n'); out.append(doubleToString(wq)).append('\n'); out.append(doubleToString(ws)).append("\n\n"); int_mu_max += 10; }
System.out.println(out.toString()); } } Расчеты по (7) сводятся в таблицу 1. Таблица 1. Пример расчетов для модели S(λmin, λmax, μmin, μmax, ∆μ)
Вывод. Разработана аналитическая модель узла однородной вычислительной сети под воздействием ВА как СМО G/G/1. Перспективой дальнейших изысканий по данной тематике станет разработка аналитической модели однородной вычислительной сети.
Ключевые слова: однородная сеть; распределенные системы, среды и сети; адаптивный выбор вариантов; полумарковские и немарковские системы массового обслуживания. Node of homogeneous computer network under the influence of virus attacks like the G/G/1 system К.S. Tkachenko, 1st cat. Engineer, graduate student, Sevastopol National Technical University, tkachenkokirillstanislavovich@mail.ru Annotation. Analytical model of homogeneous computer network node under the influence of a virus attack from the standpoint of the queuing system theory as the G/G/1 system proposed and considered. Necessary formulas, figures and tables are given. Кеуwords: homogeneous network; distributed systems, environments and networks; adaptive decision making; semi-Markov and non-Markov queuing systems. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ТКАЧЕНКО К.С., инженер 1-й категории, аспирант, Севастопольский национальный технический университет, 
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
