|
|
|
|||||||||||||
|
|
Блочные шифры В данной статье приводится краткая характеристика алгоритмов симметричного и асимметричного шифрования, рассматриваются перспективные направления развития современной криптографии, а также приводится блок-схема и программная реализация симметричного алгоритма шифрования TEA. Основным методом защиты информации от угрозы нарушения ее конфиденциальности является шифрование. Шифрование – это процесс криптографического преобразования информации в соответствии с определенным алгоритмом, при этом результат преобразования зависит от используемого ключа шифрования. Алгоритмы шифрования можно разделить на две основные категории:
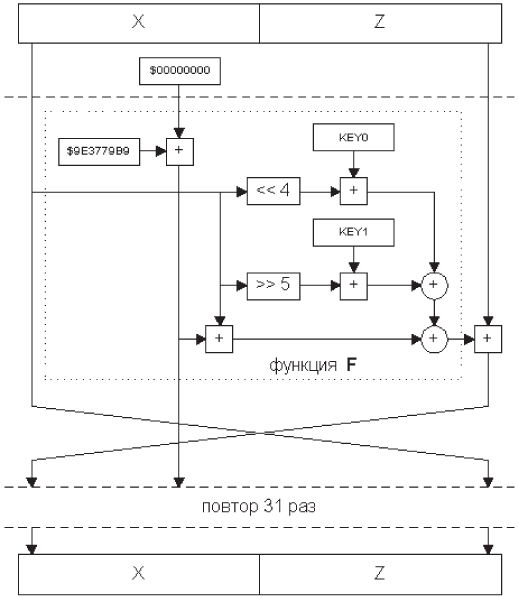
Симметричные алгоритмы. Основные стандарты и проблема использования Симметричные алгоритмы шифрования получили чрезвычайно широкое распространение благодаря высоким показателям стойкости шифрования и простоты как в аппаратной, так и в программной реализациях. Характерной особенностью симметричных алгоритмов является то, что исходное сообщение предварительно разбивается на блоки фиксированного размера, из-за чего эти алгоритмы получили название блочных шифров. В качестве примеров симметричных алгоритмов шифрования можно привести отечественный стандарт ГОСТ 28147-89 и наиболее известный стандарт шифрования DES (Data Encryption Standart), долгое время являвшийся основным стандартом шифрования в мире. Однако стремительный рост вычислительных возможностей современных ЭВМ привел к тому, что взлом алгоритма DES методом полного перебора в реальном масштабе времени перестал быть непосильной задачей, и соответственно криптографическая стойкость DES перестала удовлетворять требованиям, предъявляемым к международному стандарту. Кроме того, появились алгоритмы, превосходящие DES по всем параметрам. Учитывая данный факт, Национальный институт стандартизации и технологий США (NIST, National Institute of Standards and Technology) в 1997 году объявил открытый конкурс на новый стандарт симметричного алгоритма шифрования США. Победитель конкурса получал статус нового стандарта шифрования AES (Advanced Encryption Standard) и автоматически становился de-facto общемировым стандартом шифрования. Требования к новому стандарту шифрования были весьма простыми: алгоритм должен иметь размер блока 64 бит и поддерживать ключи шифрования длиной 128, 196 и 256 бит. В конкурсе принимали участие 15 алгоритмов, и только 5 из них прошли во второй этап. Все эти 5 алгоритмов обладали исключительной криптографической стойкостью:
По итогам конкурса, новым стандартом блочного шифрования был объявлен алгоритм RIJNDAEL. С алгоритма RIJNDAEL по условиям конкурса сняты все патентные ограничения, и сам алгоритм получил почетное второе именование: Advanced Encryption Standard – AES. Симметричные алгоритмы шифрования характеризуются тем, что используют один и тот же ключ как для шифрования, так и для расширования информации. Таким образом, любой обладатель ключа может получить доступ к конфиденциальной информации. Отсюда и вытекает главная проблема использования симметричных алгоритмов – ключ должен быть доступен только тем, кому адресована информация, и никому более, поэтому ключ является секретным. Любая утечка (или даже подозрение об утечке) ключевых данных приводит к компрометации всей сети связи и требует немедленной замены ключей на всех узлах сети. Таким образом, использование симметричных алгоритмов шифрования требует наличия целой системы распределения ключей, которая представляет собой комплекс организационно-технических мер, направленных на предотвращение возможности утечки и компрометации секретных ключей. Симметричные алгоритмы шифрования идеально подходят для шифрования информации «для себя», например, с целью предотвратить несанкционированный доступ к ней в отсутствие владельца. Это может быть как шифрование выбранных файлов, так и прозрачное шифрование целых логических или физических дисков. Асимметричные алгоритмы Асимметричные алгоритмы используют сложный математический аппарат, вследствие чего являются более ресурсоемкими и медленными по сравнению с симметричными алгоритмами, однако они позволяют преодолеть недостаток, присущий симметричным алгоритмам, за счет использования двух ключей – открытого ключа и секретного ключа. Открытый ключ предназначен для шифрования информации. Любой желающий может получить доступ к открытому ключу и зашифровать при помощи этого ключа информацию. Расшифровать эту информацию можно только при помощи секретного ключа, доступ к которому должен иметь только владелец. Очевидно, что сохранить в секрете единственный ключ, без необходимости его передачи кому-либо, намного проще, чем организовать безопасную систему распределения секретных ключей, как в симметричных алгоритмах. Однако и здесь не все так хорошо, как хотелось бы – существует угроза подмены открытого ключа, и это приводит к тому, что вся корреспонденция, направленная владельцу ключа, будет проходить через руки злоумышленника со всеми вытекающими отсюда последствиями. Для борьбы с подменой открытых ключей создаются центры сертификации. Перспективы развития современной криптографии Наиболее перспективным направлением развития криптографии с открытым ключом является использование эллиптических кривых (ECC, Elliptic Curves Cryptography). Как сообщает Computerra (www.computerra.ru), в 2003 году Агентство национальной безопасности США купило лицензию на коммерческую криптотехнологию ECC у канадской фирмы Certicom (http://www.certicom.com), основанной в 1985 году группой ученых-математиков для коммерциализации своего изобретения в области шифрования с открытым ключом – криптосистемы на эллиптических кривых, или ECC (elliptic curve cryptography). Стойкость шифрования системы ECC базируется на сложности задачи дискретного логарифмирования, при этом высокая стойкость криптосистемы достигается при значительно меньших длинах ключей, нежели в RSA. Согласно рекомендациям Национального института стандартов и технологий (НИСТ) США, эквивалентом 1024-битного ключа RSA, к примеру, является ECC-ключ длиной всего 163 бита (соотношение 6:1). Причем зависимость эта нелинейна, так что для 512-битного ключа ECC размер аналога в системе RSA составляет уже 15360 бит (соотношение 30:1). Столь выдающиеся характеристики делают ECC особенно привлекательной для применения в тех аппаратных условиях, где предъявляются строгие ограничения на размер памяти и объем допустимых вычислительных ресурсов (устройства типа смарт-карт). Широкому внедрению ECC долго мешала слабая изученность математического фундамента криптосистемы, но поскольку двадцать лет серьезнейших исследований не выявили в технологии слабостей, сегодня, по мнению многих криптографов, ее можно считать вполне зрелой. Очевидным подтверждением тому стал и нынешний выбор АНБ, за 25 млн. долларов купившего у Certicom неэксклюзивную лицензию на эллиптические кривые и, если верить сообщениям, намеренного использовать в своих шифрсредствах 512-битные ключи ECC. По условиям контракта АНБ получило права на сублицензирование технологии своим собственным клиентам, имеющим дело с национальной безопасностью. В разное время лицензии на ECC приобрели более трехсот фирм, включая Cisco Systems, Motorola, Oracle, Palm и Texas Instruments. Еще одно перспективное направление современной криптографии – квантовая криптография. Это направление позволяет обеспечить безопасную передачу ключевых данных по волоконно-оптическому кабелю. Суть заключается в следующем: информация о ключе кодируется в одном-единственном фотоне света, который затем передается получателю. Согласно законам квантовой физики, невозможно измерить один параметр фотона, не исказив при этом другой. Поэтому попытка перехвата ключа неминуемо спровоцирует нарушения в квантовой системе и приведет к искажению передаваемой информации. Таким образом, факт проникновения в систему можно достаточно легко установить, а обменивающимся сторонам придется только повторить сеанс связи с другим ключом (www.computerra.ru). Алгоритм TEA Алгоритм TEA (Tiny Encryption Algorithm) относится к классу симметричных алгоритмов. Этот алгоритм был разработан в Кембриджском университете как классическая сеть Фейштеля с оптимизацией под 32-разрядные микропроцессоры. Размер блока – 64 бит, длина ключа – 128 бит. В алгоритме использована сеть Фейштеля с двумя ветвями в 32 бита каждая. Образующая функция F обратима. Сеть Фейштеля несимметрична из-за использования в качестве операции наложения не исключающего «ИЛИ», а арифметического сложения. Сеть Фейштеля является модификацией метода смешивания текущей части шифруемого блока с результатом некоторой функции. Данная функция вычисляется от другой независимой части блока. Этот метод часто используется, потому что обеспечивает многократное использовании ключа и материала исходного блока информации. Рисунок 1. Схема работы алгоритма TEA Недостатком алгоритма является некоторая медлительность, вызванная необходимостью повторять цикл Фейштеля 32 раза (это необходимо для тщательного «перемешивания данных» из-за отсутствия табличных подстановок). Рассмотрим примеры реализации данного алгоритма на языках Паскаль и ассемблере. Рассмотрим листинг на языке Паскаль (tea.pas): const Delta=$9E3779B9; procedure EnCrypt(var y,z:longword; k0,k1,k2,k3:longword); var a,sum:longword; begin sum:=0; for a:=0 to 31 do begin inc(sum,Delta); inc(y,((z shl 4)+k0) xor (z+sum) xor ((z shr 5)+k1)); inc(z,((y shl 4)+k2) xor (y+sum) xor ((y shr 5)+k3)); end; end;
procedure DeCrypt(var y,z:longword; k0,k1,k2,k3:longword); var a,sum:longword; begin sum:=Delta shl 5; for a:=0 to 31 do begin dec(z,((y shl 4)+k2) xor (y+sum) xor ((y shr 5)+k3)); dec(y,((z shl 4)+k0) xor (z+sum) xor ((z shr 5)+k1)); dec(sum,Delta); end; end; Рассмотрим листинг на ассемблере (tea_128.asm): ;--------------------------------------------------------; ; BUFFER TO ENCRYPT -> EDX ; ; KEY TO ENCRYPT -> EAX ; ; SIZE OF BUFFER (div 4 = 0) -> ECX ; ;--------------------------------------------------------; total_encrypt: pusha ; Сохраняем всё в стеке mov esi,eax ; Кладем в esi – eax mov edi,edx ; Кладём в edi – edx work__: pusha ; Сохраняем всё в стеке call Encrypt ; Шифруем первые 64 бита данных popa ; Восстанавливаем из стека add edi,8 ; Добавляем к edi – 8 sub ecx,7 ; Отнимаем от ecx – 7 loop work__ ; Продолжаем шифровать popa ; Восстанавливаем из стека ret ; Возврат из подпрограммы ;--------------------------------------------------------; ; BUFFER TO DECRYPT -> EDX ; ; KEY TO DECRYPT -> EAX ; ; SIZE OF BUFFER (div 4 = 0) -> ECX ; ;--------------------------------------------------------; total_decrypt: pusha ; Сохраняем всё в стеке mov esi,eax ; Кладём в esi – eax mov edi,edx ; Кладём в edi – edx work2__: pusha ; Сохраняем всё в стеке call decrypt ; Шифруем первые 64 бита данных popa ; Восстанавливаем из стека add edi,8 ; Добавляем к edi – 8 sub ecx,7 ; Отнимаем от ecx – 7 loop work2__ ; Продолжаем шифровать
popa ; Восстанавливаем из стека ret ; Возврат из подпрограммы ;--------------------------------------------------------; Encrypt: push edi ; Сохраняем edi в стеке mov ebx,v0 ; Кладем в ebx первые 32 бита данных mov ecx,v1 ; В ecx кладем вторые 32 бита данных xor eax,eax ; Обнуляем eax mov edx,9e3779b9h ; В edx -> sqr(5)-1 * 231 mov edi,32 ; Кладем в edi - 32 ELoopR: add eax,edx ; Добавляем к eax – edx mov ebp,ecx ; Кладём в ebp – ecx shl ebp,4 ; Сдвиг ebp на 4 бита влево add ebx,ebp ; Добавляем к ebx – ebp mov ebp,k0 ; Кладём в ebx первые 32 бита ключа xor ebp,ecx ; Сравниваем их со вторыми 32 битами данных add ebx,ebp ; Добавляем к первым 32 битам данных результат mov ebp,ecx ; Кладём в ebp – ecx shr ebp,5 ; Делим ebp на 32 xor ebp,eax ; Сравниваем ebp с eax add ebx,ebp ; Добавляем к ebx – ebp add ebx,k1 ; Добавляем к ebx – вторые 32 бита ключа ; mov ebp,ebx ; Кладем в ebp – ebx shl ebp,4 ; Сдвиг ebp на 4 бита влево add ecx,ebp ; Добавляем к ecx – ebp mov ebp,k2 ; Кладем в ebp третьи 32 бита ключа xor ebp,ebx ; Сравниваем ebp с ebx add ecx,ebp ; Добавляем к ecx – ebp mov ebp,ebx ; Кладем в ebp – ebx shr ebp,5 ; Сдвиг ebp вправо на 5 бит xor ebp,eax ; Сравниваем ebp с eax add ecx,ebp ; Добавляем к ecx – ebp add ecx,k3 ; Добавляем к ecx – четвёртые 32 бита ключа dec edi ; Уменьшаем edi на единицу jnz ELoopR ; Шифруем дальше pop edi ; Вынимаем из стека edi mov v0,ebx ; Кладем результаты шифрования в отведённое mov v1,ecx ; для них место ret ; Возврат из подпрограммы ;-------------------------------------------------------; Decrypt: push edi ; Сохраняем edi в стеке mov ebx,v0 ; Кладем в ebx первые 32 бита данных mov ecx,v1 ; В ecx кладем вторые 32 бита данных mov edx,9e3779b9h ; В edx -> sqr(5)-1 * 231 mov eax,edx ; Кладем в eax – ed shl eax,5 ; Сдвиг eax влево на 5 бит mov edi,32 ; Кладем в edi – 32 DLoopR: mov ebp,ebx ; Кладем в ebp – ebx shl ebp,4 ; Сдвиг ebp на 4 бита влево sub ecx,ebp ; Отнимаем от ecx – ebp mov ebp,k2 ; Кладем в ebp третьи 32 бита ключа xor ebp,ebx ; Сравниваем ebp с ebx sub ecx,ebp ; Отнимаем от ecx – ebp mov ebp,ebx ; Кладем в ebp – ebx shr ebp,5 ; Сдвиг ebp вправо на 5 бит xor ebp,eax ; Сравниваем ebp с eax sub ecx,ebp ; Отнимаем от ecx – ebp sub ecx,k3 ; Отнимаем от ecx – четвёртые 32 бита ключа ; mov ebp,ecx ; Кладем в ebp – ecx shl ebp,4 ; Сдвиг ebp на 4 бита влево sub ebx,ebp ; Отнимаем от ebx – ebp mov ebp,k0 ; Кладем в ebx первые 32 бита ключа xor ebp,ecx ; Сравниваем ebp с eсx sub ebx,ebp ; Отнимаем от ebx – ebp mov ebp,ecx ; Кладём в ebp – ecx shr ebp,5 ; Сдвиг ebp вправо на 5 бит xor ebp,eax ; Сравниваем ebp с eax sub ebx,ebp ; Отнимаем от ebx – ebp sub ebx,k1 ; Отнимаем от ebx – вторые 32 бита ключа sub eax,edx ; Отнимаем от eax – edx dec edi ; Уменьшаем edi на единицу jnz DLoopR ; Дешифруем дальше pop edi ; Вынимаем из стека edi mov v0,ebx ; Кладём результаты шифрования в отведённое mov v1,ecx ; для них место ret ; Возврат из подпрограммы ;-------------------------------------------------------; v0 equ dword ptr [edi] v1 equ dword ptr [edi+4] k0 equ dword ptr [esi] k1 equ dword ptr [esi+4] k2 equ dword ptr [esi+8] k3 equ dword ptr [esi+12] Как вы могли заметить, алгоритм довольно-таки простой и легко реализуем на ассемблере. Теперь на базе данного алгоритма разработаем утилиту для шифрования файлов, ориентированную на ОС Windows. Рассмотрим листинг (fencu.asm): ;--------------------------------------------------------; ; BUFFER TO ENCRYPT -> EDX ; ; KEY TO ENCRYPT -> EAX ; ; SIZE OF BUFFER (div 4 = 0) -> ECX ; ;--------------------------------------------------------; total_encrypt: pusha ; Сохраняем всё в стеке mov esi,eax ; Кладем в esi – eax mov edi,edx ; Кладём в edi – edx work__: pusha ; Сохраняем всё в стеке call Encrypt ; Шифруем первые 64 бита данных popa ; Восстанавливаем из стека add edi,8 ; Добавляем к edi – 8 sub ecx,7 ; Отнимаем от ecx – 7 loop work__ ; Продолжаем шифровать popa ; Восстанавливаем из стека ret ; Возврат из подпрограммы ;--------------------------------------------------------; ; BUFFER TO DECRYPT -> EDX ; ; KEY TO DECRYPT -> EAX ; ; SIZE OF BUFFER (div 4 = 0) -> ECX ; ;--------------------------------------------------------; total_decrypt: pusha ; Сохраняем всё в стеке mov esi,eax ; Кладём в esi – eax mov edi,edx ; Кладём в edi – edx work2__: pusha ; Сохраняем всё в стеке call decrypt ; Шифруем первые 64 бита данных popa ; Восстанавливаем из стека add edi,8 ; Добавляем к edi – 8 sub ecx,7 ; Отнимаем от ecx – 7 loop work2__ ; Продолжаем шифровать
popa ; Восстанавливаем из стека ret ; Возврат из подпрограммы ;--------------------------------------------------------; Encrypt: push edi ; Сохраняем edi в стеке mov ebx,v0 ; Кладем в ebx первые 32 бита данных mov ecx,v1 ; В ecx кладем вторые 32 бита данных xor eax,eax ; Обнуляем eax mov edx,9e3779b9h ; В edx -> sqr(5)-1 * 231 mov edi,32 ; Кладем в edi - 32 ELoopR: add eax,edx ; Добавляем к eax – edx mov ebp,ecx ; Кладём в ebp – ecx shl ebp,4 ; Сдвиг ebp на 4 бита влево add ebx,ebp ; Добавляем к ebx – ebp mov ebp,k0 ; Кладём в ebx первые 32 бита ключа xor ebp,ecx ; Сравниваем их со вторыми 32 битами данных add ebx,ebp ; Добавляем к первым 32 битам данных результат mov ebp,ecx ; Кладём в ebp – ecx shr ebp,5 ; Делим ebp на 32 xor ebp,eax ; Сравниваем ebp с eax add ebx,ebp ; Добавляем к ebx – ebp add ebx,k1 ; Добавляем к ebx – вторые 32 бита ключа ; mov ebp,ebx ; Кладем в ebp – ebx shl ebp,4 ; Сдвиг ebp на 4 бита влево add ecx,ebp ; Добавляем к ecx – ebp mov ebp,k2 ; Кладем в ebp третьи 32 бита ключа xor ebp,ebx ; Сравниваем ebp с ebx add ecx,ebp ; Добавляем к ecx – ebp mov ebp,ebx ; Кладем в ebp – ebx shr ebp,5 ; Сдвиг ebp вправо на 5 бит xor ebp,eax ; Сравниваем ebp с eax add ecx,ebp ; Добавляем к ecx – ebp add ecx,k3 ; Добавляем к ecx – четвёртые 32 бита ключа dec edi ; Уменьшаем edi на единицу jnz ELoopR ; Шифруем дальше pop edi ; Вынимаем из стека edi mov v0,ebx ; Кладем результаты шифрования в отведённое mov v1,ecx ; для них место ret ; Возврат из подпрограммы ;-------------------------------------------------------; Decrypt: push edi ; Сохраняем edi в стеке mov ebx,v0 ; Кладем в ebx первые 32 бита данных mov ecx,v1 ; В ecx кладем вторые 32 бита данных mov edx,9e3779b9h ; В edx -> sqr(5)-1 * 231 mov eax,edx ; Кладем в eax – ed shl eax,5 ; Сдвиг eax влево на 5 бит mov edi,32 ; Кладем в edi – 32 DLoopR: mov ebp,ebx ; Кладем в ebp – ebx shl ebp,4 ; Сдвиг ebp на 4 бита влево sub ecx,ebp ; Отнимаем от ecx – ebp mov ebp,k2 ; Кладем в ebp третьи 32 бита ключа xor ebp,ebx ; Сравниваем ebp с ebx sub ecx,ebp ; Отнимаем от ecx – ebp mov ebp,ebx ; Кладем в ebp – ebx shr ebp,5 ; Сдвиг ebp вправо на 5 бит xor ebp,eax ; Сравниваем ebp с eax sub ecx,ebp ; Отнимаем от ecx – ebp sub ecx,k3 ; Отнимаем от ecx – четвёртые 32 бита ключа ; mov ebp,ecx ; Кладем в ebp – ecx shl ebp,4 ; Сдвиг ebp на 4 бита влево sub ebx,ebp ; Отнимаем от ebx – ebp mov ebp,k0 ; Кладем в ebx первые 32 бита ключа xor ebp,ecx ; Сравниваем ebp с eсx sub ebx,ebp ; Отнимаем от ebx – ebp mov ebp,ecx ; Кладём в ebp – ecx shr ebp,5 ; Сдвиг ebp вправо на 5 бит xor ebp,eax ; Сравниваем ebp с eax sub ebx,ebp ; Отнимаем от ebx – ebp sub ebx,k1 ; Отнимаем от ebx – вторые 32 бита ключа sub eax,edx ; Отнимаем от eax – edx dec edi ; Уменьшаем edi на единицу jnz DLoopR ; Дешифруем дальше pop edi ; Вынимаем из стека edi mov v0,ebx ; Кладём результаты шифрования в отведённое mov v1,ecx ; для них место ret ; Возврат из подпрограммы ;-------------------------------------------------------; v0 equ dword ptr [edi] v1 equ dword ptr [edi+4] k0 equ dword ptr [esi] k1 equ dword ptr [esi+4] k2 equ dword ptr [esi+8] k3 equ dword ptr [esi+12] Итак, к чему мы пришли в итоге – мы смогли написать утилиту, которая шифрует файлы по алгоритму TEA на основе 128-битного ключа. Вскрытие таких файлов нельзя назвать невозможным, но можно назвать крайне трудоемким и временеемким, базируясь на текущих разработках. Данную утилиту можно было бы оптимизировать таким образом, чтобы ключи хранить на дискете. При этом необходимо обеспечить безопасное хранение этой дискеты, чтобы она не попала в руки злоумышленника. Кроме того, если дискета потеряется или испортится, то доступ к зашифрованным файлам станет невозможным. Именно поэтому решать использовать внешний носитель для хранения секретного ключа или нет – дело каждого из нас. Что касается меня, то я больше доверяю своей памяти. Отдельное спасибо Владимиру Мешкову за помощь в подготовке статьи. |
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 СТАНИСЛАВ ГОШКО
СТАНИСЛАВ ГОШКО