 |
|
|
|
Система распределения секрета на основе кодов, исправляющих ошибки
Система распределения секрета Новая система распределения секрета, представленная в статье, работает на основе кодов, исправляющих ошибки. Целью исследования является разработка высокопроизводительной системы, которая будет использовать разные коды, исправляющие ошибки В настоящее время значительная часть глобального обмена данными происходит через открытые сетевые соединения. Большое количество данных доступно практически всем. Необходимо гарантировать информационную безопасность и защиту [1]. Вместе с применением шифрования, секретные ключи должны храниться в защищенном хранилище. Секретные ключи непосредственно не должны быть доступны где-либо в системе без заранее обеспеченной физической защиты. Увы, это условие практически не выполнимо. В целях обеспечения безопасности ключей применяются пороговые схемы разделения секрета: ключ делится на несколько частей и хранится в разных местах. Более популярной пороговой схемой разделения секрета является схема разделения Шамира, но схема Шамира работает достаточно медленно, так как она основана на полиномиальных операциях, и производительность низка, когда значение порога высоко. Предлагается новая пороговая схема разделения секрета, которая основана на кодах, исправляющих ошибки. Так как коды, исправляющие ошибки, главным образом используют логические операции, которые выполняются быстрее на компьютере, поэтому данный метод работает быстрее, чем метод Шамира. Коды В этой системе используются следующие коды:
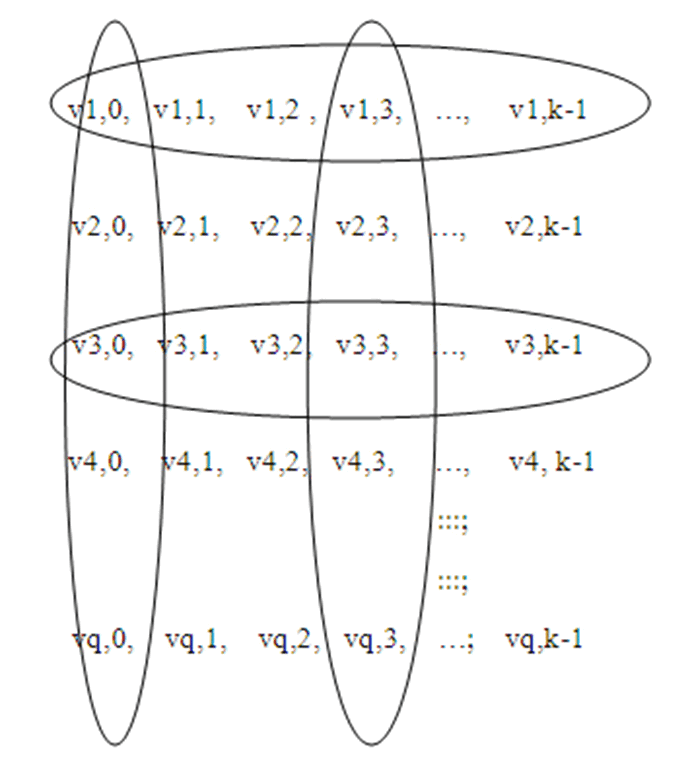
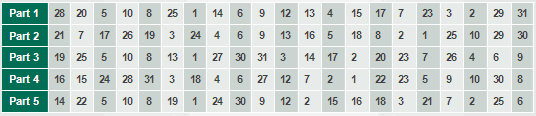
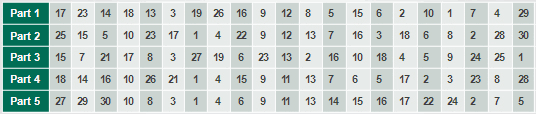
Метод разделения Ниже описывается принцип работы метода разделения секрета на примере кода БЧХ(21,31,2). После кодирования 21-битной исходной информации получим 31-битную кодированную информацию, которую назовем кодовым словом. Это позволит нам корректировать любых два ошибочных бита. Каждый 21 бит секретного файла (который надо разделить) кодируется кодом БЧХ(21,31,2), и получаются соответствующие 31-битовые кодовые слова. Эти кодовые слова представим в виде матрицы, как показано на рис. 1. Понятно, что этот файл после кодирования кодом БЧХ(21,31,2) нам надо разделить.
Рисунок 1. Структура кодированного файла В этом примере «k» – длина кодового слова (в данном случае k = 31), а «q» зависит от объема исходного файла. Каждая строка массива представляет собой кодовое слово кода БЧХ(21,31,2), это означает, что любые две ошибки могут быть исправлены в этих 31 битах. На основе этой характеристики мы можем распределить по столбцам. Если рассматривать каждый столбец в качестве отдельного компонента, то очевидно, что мы можем восстановить оригинальный файл в случае повреждения или потери любых двух компонентов. Это приводит к 29/31 пороговой схеме. Процесс разделения Чтобы увеличить безопасность и иметь компоненты, равные по объему распределяемого файла, мы должны применить группировку по определенному методу. От каждой части 21 столбцов должны быть взяты данные (с определенным методом), для удовлетворения всех требований. Например, в случае группировки согласно таблице 1 мы получим 4/3 пороговую схему. Таблицa 1. Пороговая схема 4/3
Каждая строка представляет собой отдельную часть (компонент). Как мы видим, часть 1 содержит количество столбцов, взятых с определенным методом. Таблица 1 показывает, что после слияния любых трех частей, у нас будет 29 частей, и две части будут отсутствовать. При использовании алгоритма декодирования кода БЧХ(21,31,2) мы можем восстановить две недостающие (испорченные) части. Оказывается, распределение секрета в соответствии с таблицей 1 приводит к пороговой схеме 4/3. Секретный файл разделен на четыре части так, что любые три части достаточны для восстановления. Таблица 2 представляет 5/3 пороговую схему. Таблица 2. Пороговая схема 5/3
Таблица 3 представляет 5/4 пороговую схему. Таблицa 3. Пороговая схема 5/4
Тот же метод разделения секрета применим для других кодов, исправляющих ошибки. В дальнейшем планируется внедрять другие коды тоже, сравнить все коды по быстродействиям. Система станет автоматически выбирать тот код, который в данном случае будет самым быстрым. Эти действия будут невидимы для пользователя. Продолжая исследования, станем проводить разные сравнительные тесты по разным параметрам с методами Шамира и с другими методами разделения секрета. *** Итак, мы имеем новую систему для разделения секрета. Этот метод намного быстрее, так как использует коды, исправляющие ошибки, а эти коды используют логические операции. Продолжая исследование, будем тестировать этот метод с методом Шамира по разным параметрам.
Ключевые слова: распределение секрета, коды, обнаружение и исправление ошибок, пороговая схема. |
АРТАК ХЕМЧЯН, Государственный инженерный университет Армении, 
СЕВАК АРУТЮНЯН, обладатель второго места регионального тура «Россия и СНГ». Государственный инженерный университет Армении, 
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|
