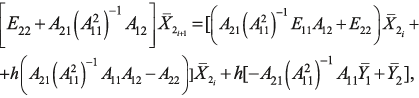|
|
|
|||||||||||||
|
|
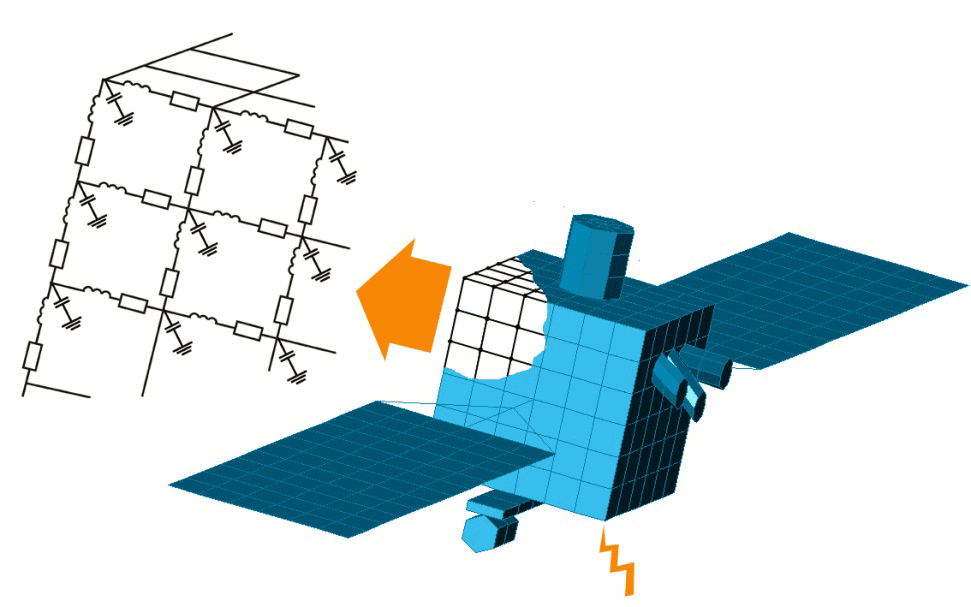
ЖАДОВ А.Д., ВОСТРИКОВ А.В., БОРИСОВ Н.И., ТУМКОВСКИЙ С.Р. Программная реализация редуцированной вычислительной схемы В работе рассмотрена реализация основных алгоритмов построения редуцированной вычислительной схемы численного интегрирования системы линейных дифференциальных уравнений на основе методов Эйлера. Приведены временные затраты на построение и расчет по редуцированной схеме по сравнению с традиционными численными методами. Расчет по вычислительной схеме больших математических моделей происходит на два-три порядка быстрее используемых в специализированном программном обеспечении методов Одними из важнейших проблем длительной эксплуатации космических аппаратов (КА) являются электризация и связанные с этим процессом электростатические разряды (ЭСР). В 30% случаев потеря КА происходит из-за электризации. ЭСР порождают токи на поверхности КА, которые наводят в бортовой кабельной сети наводки величиной до 10 В. Помехи такой величины способны привести к отказам бортовой радиоэлектронной аппаратуры. Для сведения: к минимуму возможных сбоев электроники КА необходимо смоделировать картину растекания тока по поверхности КА. Далее проводится расчет наводок в кабелях и даются рекомендации по их экранированию или оптимальному маршруту прокладки. С этой целью в МИЭМ были разработаны структурная электрофизическая модель (СЭМ) КА [1] и программное обеспечение ПО «Satellite-MIEM» для ее реализации. ПО «Satellite-MIEM» синтезирует структурную электрофизическую модель (СЭМ) на базе заданной полигональной 3D-модели КА (см. рис. 1). Полигональная модель состоит из совокупности элементарных фигур – треугольников или прямоугольников, преобразуемых средствами программы в поверхностную сетку: совокупность связанных узлов. Сетка является равномерной, то есть шаги по всем координатам равны между собой. Ячейка сетки представляется прямоугольником или треугольником. Количество узлов СЭМ крупногабаритного КА будет равняться (1…2)х105. Каждая связь (ветвь) представляется в виде элементов электрической цепи (R, L, C), в целом образующих эквивалентную электрическую схему поверхности КА. При этом номиналы элементов одного типа одинаковы. Рисунок 1. Преобразование полигональной модели в СЭМ С помощью ПО «Satellite-MIEM», зная место электрического разряда, можно получить картину растекания тока. Для расчета переходных токов используется наиболее производительная программа расчета электрических схем LTSpice, однако для анализа схемы из 150 000 узлов требуется 83 часа (эксперимент проводился на ЭВМ с двуядерным процессором с тактовой частотой 1,8 ГГц на каждом ядре, объем оперативной памяти равняется 2 Гб) [2], что неприемлемо для предприятий космической отрасли. Используемые в ПО численные методы хорошо показывают себя только при расчете небольших моделей [3]. Поэтому возникает необходимость в создании новых методов расчета больших электрических схем. Ранее в [4-6] был предложен новый подход редукции модели линейной схемы, основанный на исключении из модели подвекторов, содержащих в себе фазовые переменные, значения которых не превышают 1-2% от величины приложенного к месту разряда тока. В данной работе авторы разрабатывают программу для реализации редуцированной вычислительной схемы и проверяют теоретические оценки эффективности вычислительной схемы на практике. 1. Построение редуцированной вычислительной схемы Модель ЭЭС КА может быть сформирована в расширенном однородном координатном базисе (РОКБ) и записана в виде системы линейных обыкновенных дифференциальных уравнений [4]:
где С, G – числовые матрицы порядка Отметим специфику модели схемы. 1) Матрица С является диагональной и вырожденной. Диагональ состоит из двух групп коэффициентов и коэффициенты внутри каждой группы одинаковы. 2) Матрица G – невырожденная, симметричная и разреженная матрица. 3) Вектор Необходимо с минимальными временными затратами выполнить решение системы уравнений в момент времени t*, т.е. вычислить числовой вектор 2. Редукция вычислительной схемы методов Эйлера Для решения задачи (1) формируется модель схемы в РОКБ следующим образом:
Отметим, что матрицы – симметричные, подматрицы C11, L22, G33 – диагональные, при этом:
Модель (2) записывается в виде:
Исключаем из модели подвектор
Подстановка
(7)
или
где r – сопротивление резисторов в схеме. Модель может быть записана в виде системы дифференциальных уравнений, заданной в явной форме:
где Будем считать, что исходная задача имеет следующий вид:
При использовании численных методов процесс решения (11) заключается в вычислении вектора решения в моменты времени Рассмотрим одношаговый метод Эйлера для решения задачи (11). Явный метод Эйлера решения системы уравнений с учетом конкретного вида системы уравнений (11):
Рассмотрим неявный метод Эйлера. С учетом конкретного вида системы уравнений (11) получим следующую формулу метода Эйлера:
Для построения новой вычислительной схемы необходимо преобразовать задачи (12) и (13) в некоторую редуцированную модель (макромодель) КА, количество уравнений в которой будет равно
(второй этап редукции модели), что снижает трудоемкость вычислений на два-три порядка. Для этого запишем оба вида вычислительных процессов в блочной форме:
где Пусть подвекторы
или
3. Программная реализация редуцированной вычислительной схемы Для реализации редуцированной вычислительной схемы для расчета линейных ЭЭС большой размерности нами было разработано программное обеспечение, которое позволяет:
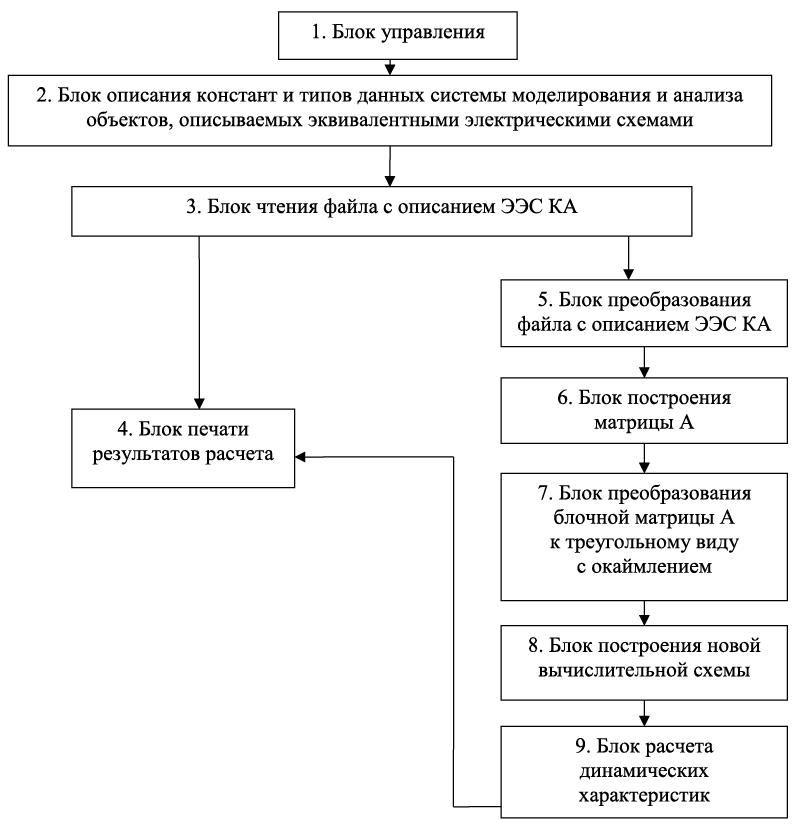
Иерархическую структуру разработанной программы покажем на рис. 2. Рисунок 2. Иерархическая структура разработанной программы Разработанное ПО для получения требуемого результата выполняет ряд этапов:
Рассмотрим алгоритм конвертирования файла LTSpice в удобный для дальнейших преобразований матричный вид и результат его выполнения (см. рис. 3):
Рисунок 3. Пример результата конвертирования файла LTSpice в удобный для дальнейших преобразований матричный вид согласно (2) Преобразования матрицы А (16) отличаются от предложенных в [5], где была получена треугольная матрица с окаймлением с помощью метода определяющих величин. Предложенный алгоритм позволяет получить более выгодную с точки зрения дальнейших вычислений треугольную матрицу, но посредством арифметических операций со строками матрицы, вследствие чего может быть потеряна точность вычислений. Алгоритм и пример результата (см. рис. 4) приведены ниже:
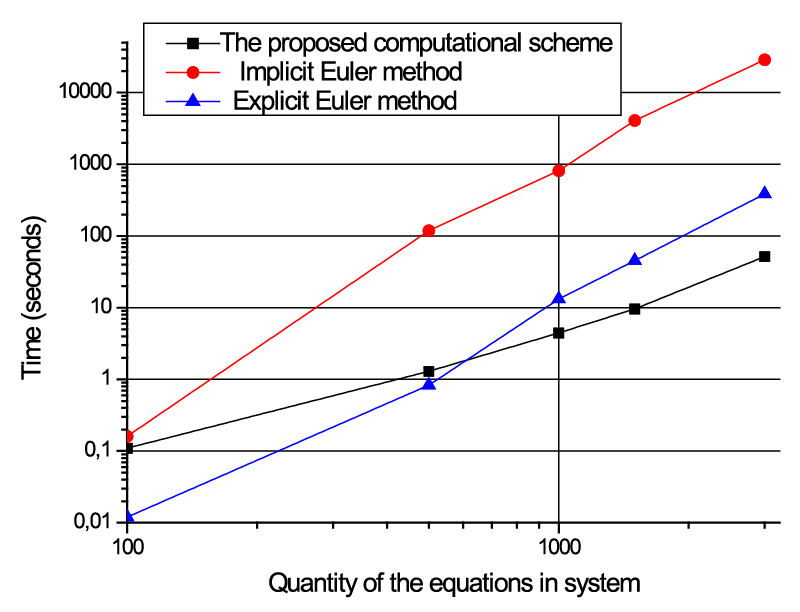
Рисунок 4. Результат преобразования матрицы На современном компьютере (ЭВМ с двуядерным процессором с тактовой частотой 1,8 ГГц на каждом ядре, объем оперативной памяти равняется 2 Гб) проведены исследования временных затрат на анализ модели ЭЭС, содержащей до 3000 обыкновенных дифференциальных уравнений. Время анализа неявным методом Эйлера, явным методом Эйлера и по предложенной новой вычислительной схеме с учетом времени построения самой вычислительной схемы показано на рис. 5. Для модели, состоящей из 100 уравнений, неявному методу Эйлера потребовалось 0,16 с для анализа, расчет по новой вычислительной схеме при размерности подматрицы (10х10) занял 0,012 с, что в 13 раз быстрее (таблица 1). Для модели из 3000 уравнений расчет неявным методом Эйлера потребовал 28397 с для анализа, вычисления по новой схеме при размерности подматрицы (10х10) затратили 387,5 с, что в 75 раз быстрее. В случае больших систем использование редуцированной схемы оказывается выгоднее на два-три порядка других неявных численных методов. При этом результат расчета в выбранной локальной области традиционными численными методами и по редуцированной вычислительной схеме совпадает. Рисунок 5. Время анализа модели ЭЭС разными методами Таблица 1. Результат тестирования численных методов на ПК
Существенно отличается время анализа явным методом Эйлера и по предложенной новой вычислительной схеме без учета времени построения самой вычислительной схемы (такой вариант используется при многократном использовании макромодели). Для модели из 3000 уравнений явному методу Эйлера потребуется 51,3 с для анализа, вычисления по новой схеме при размерности подматрицы (10х10) потребуют 0,005 с, что в 10 260 раз быстрее, в случае подматрицы (100х100) вычисления по новой схеме потребуют 2,9 с, что в 17,7 раза быстрее. На практике подматрица будет содержать менее 1% коэффициентов от их общего количества модели, поэтому выгода может достигать четырех порядков по сравнению даже с явными численными методами. Таким образом, результат тестирования подтвердил полученную теоретически в [4] эффективность редуцированной схемы. Практика показала, что расчет по вычислительной схеме больших математических моделей происходит на два-три порядка быстрее используемых в специализированном программном обеспечении методов.
Ключевые слова: алгоритм, редукция, система дифференциальных уравнений, преобразование матрицы. Software implementation of the reduced computational schemes for the numerical integration of the system of linear differential equations based on the methods of Euler Jadov A.D., Vostrikov A.V., Borisov N.I, Tumkovskiy S.R. The paper considers the implementation of the basic algorithms for constructing the reduced computational schemes for the numerical integration of the system of linear differential equations by Euler's method. Shows the time and construction costs reduced by calculation scheme as compared with conventional numerical methods. Payment scheme for computing large mathematical models occurs at 2-3 orders of magnitude faster used in specialized software techniques. Keywords: algorithm, the reduction of the system of differential equations, matrix transformation |
Комментарии отсутствуют
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










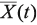 – вектор искомых фазовых переменных (напряжений во всех узлах схемы и токов, протекающих через индуктивные элементы),
– вектор искомых фазовых переменных (напряжений во всех узлах схемы и токов, протекающих через индуктивные элементы), 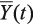 – вектор входных сигналов.
– вектор входных сигналов.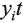 , где i может быть любым числом от 1 до n.
, где i может быть любым числом от 1 до n.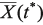 .
.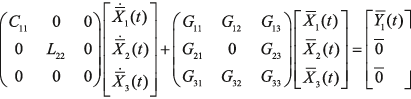 , (2)
, (2)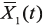 – подвектор напряжений в узлах, к которым подсоединены конденсаторы;
– подвектор напряжений в узлах, к которым подсоединены конденсаторы;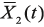 – подвектор токов, проходящих через индуктивные элементы;
– подвектор токов, проходящих через индуктивные элементы;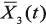 – подвектор напряжений в узлах, к которым не подсоединены конденсаторы.
– подвектор напряжений в узлах, к которым не подсоединены конденсаторы.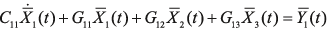 , (3)
, (3)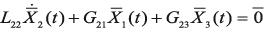 , (4)
, (4)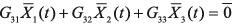 , (5)
, (5) . Из (5) получим:
. Из (5) получим: , (6)
, (6) из (6) в (3) и (4) приводит к следующим выражениям:
из (6) в (3) и (4) приводит к следующим выражениям:


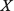




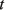



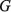



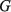


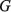




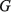



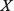



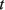



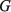



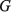


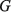




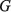



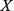



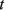


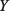



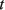

 (8)
(8)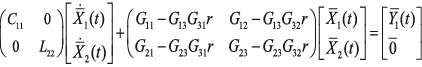 (9),
(9), , (10)
, (10)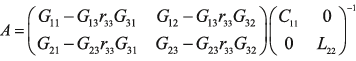
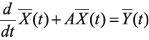 ,
,  . (11)
. (11)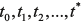 , т.е.
, т.е.  ,
, 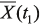 ,…,
,…, 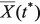 .
.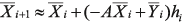 . (12)
. (12)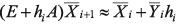 . (13)
. (13)



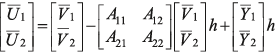 , (14)
, (14)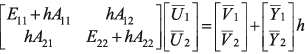 , (15)
, (15)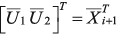 ,
, 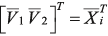 .
.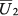 и
и  содержат по
содержат по 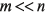 искомых коэффициентов решения. Получим на базе выражений (14) и (15) редуцированную вычислительную схему, из которой исключим подвекторы
искомых коэффициентов решения. Получим на базе выражений (14) и (15) редуцированную вычислительную схему, из которой исключим подвекторы 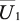 и
и 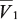 .
.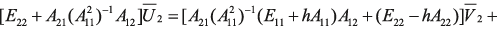
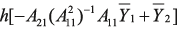 (16)
(16)