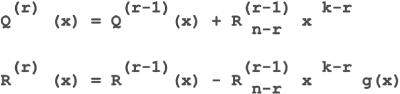|
|
|
|||||||||||||
|
|
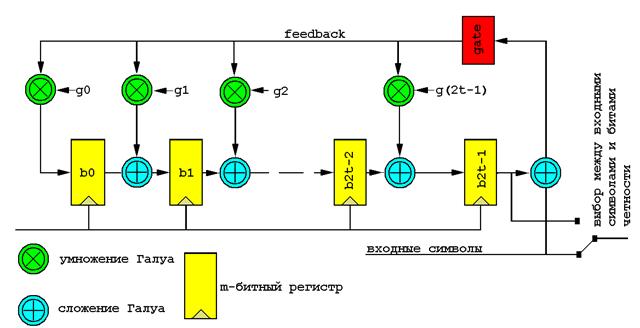
Коды Рида-Соломона в практических реализациях, или Информация, воскресшая из пепла III В прошлых статьях этого цикла мы рассмотрели базовый математический аппарат, на который опираются коды Рида-Соломона, и исследовали простейший кодер/декодер, способный исправлять одиночные ошибки и работающий с двумя символами четности. Для подавляющего большинства задач такой корректирующей способности оказывается катастрофически недостаточно, и тогда приходится задумываться о реализации более мощного кодера/декодера. Кодер/декодер, рассматриваемый в настоящей статье, чрезвычайно конфигурабелен и может быть настроен на работу с любым количеством символов четности, а это означает, что при разумной избыточности он способен исправлять любое мыслимое количество ошибок. Подобная универсальность не проходит даром, и конструкция такого декодера усложнятся более чем в сто (!) раз. Самостоятельное проектирование декодеров Рида-Соломона требует глубоких знаний высшей математики в целом и природы корректирующих кодов в частности, поэтому не смущайтесь, если данная статья поначалу вам покажется непонятной. Это действительно сложные вещи, не допускающие простого объяснения. С другой стороны, для практического использования корректирующих кодов можно и не вникать в их сущность, просто откомпилировав исходные тексты кодера/декодера Рида-Соломона, приведенные в данной статье. Также вы можете воспользоваться любой законченной библиотекой, поставляемой сторонними разработчиками. В качестве альтернативного примера в заключение этой статьи будет кратно описан интерфейс библиотеки ElByECC.DLL, разработанной компанией «Elaborate Bytes» и распространяемой вместе с популярным копировщиком Clone CD. Известнейший прожигатель дисков всех времен и народов Ahead Burning ROM имеет аналогичную библиотеку, размещенную в файле NEWTRF.DLL. Легенда Напомним читателю основные условные обозначения, используемые в этой статье. Количество символов кодируемого сообщения (называемого также информационным словом) по общепринятому соглашению обозначается буквой k; полная длина кодового слова, включающего в себя кодируемые данные и символы четности, – n. Отсюда, количество символов четности равно: n – k. За максимальным количеством исправляемых ошибок «закреплена» буква t. Поскольку для исправления одной ошибки требуется два символа четности, общее количество символов четности равно 2t. Выражение RS(n, k) описывает определенную разновидность корректирующих кодов Рида-Соломона, оперирующую с n-символьными блоками, k-символов, из которых представляют полезные данные, а все остальные задействованы под символы четности. Полином, порожденный на основе примитивного члена a, называется порожденным или сгенерированным (generate) полиномом. Кодировщик (encoder) Существует по меньшей мере два типа кодеров Рида-Соломона: несистематические и систематические кодировщики. Вычисление несистематических корректирующих кодов Рида-Соломона осуществляется умножением информационного слова на порожденный полином, в результате чего образуется кодовое слово, полностью отличающееся от исходного информационного слова, а потому для непосредственного употребления категорически непригодное. Для приведения полученных данных в исходный вид мы должны в обязательном порядке выполнить ресурсоемкую операцию декодирования, даже если данные не искажены и не требуют восстановления! При систематическом кодировании, напротив, исходное информационное слово останется неизменным, а корректирующие коды (часто называемые символами четности) добавляются в его конец, благодаря чему к операции декодирования приходится прибегать лишь в случае действительного разрушения данных. Вычисление несистематических корректирующих кодов Рида-Соломона осуществляется делением информационного слова на порожденный полином. При этом все символы информационного слова сдвигаются на n – k байт влево, а на освободившееся место записывается 2t байт остатка (см. рис. 1). Поскольку рассмотрение обоих типов кодировщиков заняло бы слишком много места, сосредоточим свое внимание на одних лишь систематических кодерах как на наиболее популярных. Рисунок 1. Устройство кодового слова Архитектурно кодировщик представляет собой совокупность сдвиговых регистров (shift registers), объединенных посредством сумматоров и умножителей, функционирующих по правилам арифметики Галуа. Сдвиговый регистр (иначе называемый регистром сдвига) представляет последовательность ячеек памяти, называемых разрядами, каждый из которых содержит один элемент поля Галуа GF(q). Содержащийся в разряде символ, покидая этот разряд, «выстреливается» на выходную линию. Одновременно с этим разряд «засасывает» символ, находящийся на его входной линии. Замещение символов происходит дискретно, в строго определенные промежутки времени, называемые тактами. При аппаратной реализации сдвигового регистра его элементы могут быть объединены как последовательно, так и параллельно. При последовательном объединении пересылка одного m-разрядного символа потребуем m-тактов, в то время как при параллельном она осуществляется всего за один такт. Низкая эффективность программных реализаций кодеров Рида-Соломона объясняется тем, что разработчик не может осуществлять параллельное объединение элементов сдвигового регистра и вынужден работать с той шириной разрядности, которую «навязывает» архитектура данной машины. Однако создать 4-элементный 8-битный регистр сдвига параллельного типа на процессорах семейства IA32 вполне реально. Цепи, основанные на регистрах сдвига, обычно называют фильтрами. Блок-схема фильтра, осуществляющего деление полинома на константу, приведена на рис. 2. Пусть вас не смущает тот факт, что деление реализуется посредством умножения и сложения. Данный прием базируется на вычислении системы двух рекуррентных равенств: Формула 1. Деление полинома на константу посредством умножения и сложения Здесь: Q(r)(x) и R(r)(x) – соответственно частное и остаток на r-шаге рекурсии. Поскольку сложение и вычитание, выполняемое по модулю два, тождественны друг другу, для реализации делителя нам достаточно иметь всего два устройства – устройство сложения и устройство умножения, а без устройства вычитания можно обойтись. После n-сдвигов на выходе регистра появляется частное, а в самом регистре окажется остаток, который и представляет собой рассчитанные символы четности (они же – коды Рида-Соломона), а коэффициенты умножения с g0 по g(2t – 1) напрямую соответствуют коэффициентам умножения порожденного полинома. Рисунок 2. Устройство простейшего кодера Рида-Соломона Простейший пример программной реализации такого фильтра приведен ниже. Это законченный кодер Рида-Соломона, вполне пригодный для практического использования. Конечно, при желании его можно было бы и улучшить, но тогда неизбежно пострадала бы наглядность и компактность листинга. Листинг 1. Исходный текст простейшего кодера Рида-Соломона /*----------------------------------------------------------------------------------------------------- * * кодировщик Рида-Соломона * ======================== * * кодируемые данные передаются через массив data[i], где i=0..(k-1), а сгенерированные символы четности * заносятся в массив b[0]..b[2*t-1]. Исходные и результирующие данные должны быть представлены * в полиномиальной форме (т.е. в обычной форме машинного представления данных). * Кодирование производится с использованием сдвигового feedback-регистра, заполненного соответствующими * элементами массива g[] с порожденным полиномом внутри, процедура генерации которого уже обсуждалась * в предыдущей статье. Сгенерированное кодовое слово описывается следующей формулой: * с(x) = data(x)*x(n-k) + b(x) * * на основе исходных текстов Simon Rockliff, от 26.06.1991, распространяемых * по лицензии GNU –––––––––––––––––––––––––––––––––––––––––––––––––––––––––---------------------------------------------*/ encode_rs() { int i, j; int feedback; // инициализируем поле бит четности нулями for (i = 0; i < n - k; i++) b[i] = 0; // обрабатываем все символы исходных данных справа налево for (i = k - 1; i >= 0; i--) { // готовим (data[i] + b[n – k –1]) к умножению на g[i], т.е. складываем очередной «захваченный» // символ исходных данных с младшим символом битов четности (соответствующего «регистру» b2t-1, // см. рис. 2) и переводим его в индексную форму, сохраняя результат в регистре feedback, // как мы уже говорили, сумма двух индексов есть произведение полиномов feedback = index_of[data[i] ^ b[n – k - 1]]; // есть еще символы для обработки? if (feedback != -1) { // осуществляем сдвиг цепи bx-регистров for (j=n-k-1; j>0; j--) // если текущий коэффициент g – это действительный (т.е. ненулевой коэффициент, // то умножаем feedback на соответствующий g-коэффициент и складываем его // со следующим элементом цепочки if (g[j]!=-1) ї b[j]=b[j-1]^alpha_to[(g[j]+feedback)%n]; else // если текущий коэффициент g – это нулевой коэффициент, выполняем один лишь // сдвиг без умножения, перемещая символ из одного m-регистра в другой b[j] = b[j-1]; // закольцовываем выходящий символ в крайний левый b0-регистр b[0] = alpha_to[(g[0]+feedback)%n]; } else { // деление завершено, осуществляем последний сдвиг регистра, на выходе регистра // будет частное, которое теряется, а в самом регистре – искомый остаток for (j = n-k-1; j>0; j--) b[j] = b[j-1] ; b[0] = 0; } } } Декодер (decoder) Декодирование кодов Рида-Соломона представляет собой довольно сложную задачу, решение которой выливается в громоздкий, запутанный и чрезвычайно ненаглядный программный код, требующий от разработчика обширных знаний во многих областях высшей математики. Типовая схема декодирования, получившая название авторегрессионого спектрального метода декодирования, состоит из следующих шагов:
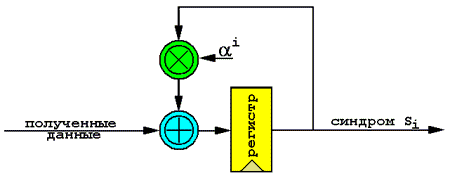
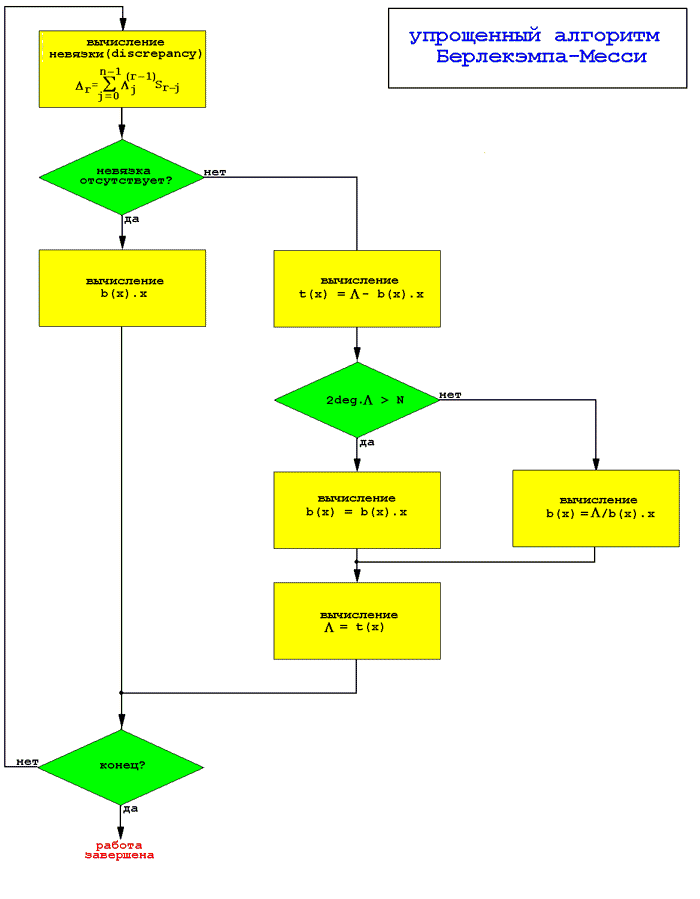
Рисунок 3. Схема авторегрессионного спектрального декодера корректирующих кодов Рида-Соломона Синдромный декодер Грубо говоря, синдром есть остаток деления декодируемого кодового слова c(x) на порожденный полином g(x), и, если этот остаток равен нулю, кодовое слово считается неискаженным. Ненулевой остаток свидетельствует о наличии по меньшей мере одной ошибки. Остаток от деления дает многочлен, не зависящий от исходного сообщения и определяемый исключительно характером ошибки (syndrome – греческое слово, обозначающее совокупность признаков и/или симптомов, характеризующих заболевание). Принятое кодовое слово v с компонентами vi = ci + ei, где i = 0, … n – 1, представляет собой сумму кодового слова c и вектора ошибок e. Цель декодирования состоит в очистке кодового слова от вектора ошибки, описываемого полиномом синдрома и вычисляемого по формуле: Sj = v(aj+j0–1), где j изменяется от 1 до 2t, а a представляет собой примитивный член «альфа», который мы уже обсуждали в предыдущей статье. Да, мы снова выражаем функцию деления через умножение, поскольку деление – крайне неэффективная в смысле производительности операция. Блок-схема устройства, осуществляющего вычисление синдрома, приведена на рис. 4. Как видно, она представляет собой типичный фильтр (сравните ее со схемой рис. 2), а потому ни в каких дополнительных пояснениях не нуждается. Рисунок 4. Блок-схема цепи вычисления синдрома Вычисление синдрома ошибки происходит итеративно, так что вычисление результирующего полинома (также называемого ответом от английского «answer») завершается непосредственно в момент прохождения последнего символа четности через фильтр. Всего требуется 2t циклов «прогона» декодируемых данных через фильтр, – по одному прогону на каждый символ результирующего полинома. Пример простой программной реализации синдромного декодера содержится в листинге 2, и он намного нагляднее его словесного описания. Полином локатора ошибки Полученный синдром описывает конфигурацию ошибки, но еще не говорит нам, какие именно символы полученного сообщения были искажены. Действительно, степень синдромного полинома, равная 2t, много меньше степени полинома сообщения, равной n, и между их коэффициентами нет прямого соответствия. Полином, коэффициенты которого напрямую соответствуют коэффициентам искаженных символов, называется полиномом локатора ошибки и по общепринятому соглашению обозначается греческой буквой L (лямбда). Если количество искаженных символов не превышает t, между синдромом и локатором ошибки существует следующее однозначное соответствие, выражаемое следующей формулой НОД[xn-1, E(x)] = L(x), и вычисление локатора сводится к задаче нахождения наименьшего общего делителя, успешно решенной еще Евклидом и элементарно реализуемой как на программном, так и на аппаратном уровне. Правда, за простоту реализации нам приходится расплачиваться производительностью, точнее непроизводительностью данного алгоритма, и на практике обычно применяют более эффективный, но и более сложный для понимания алгоритм Берлекэмпа-Месси (Berlekamp-Massy), подробно описанный Кнутом во втором томе «Искусства программирования» (см. также «Теория и практика кодов, контролирующих ошибки» Блейхута) и сводящийся к задаче построения цепи регистров сдвига с линейной обратной связью и по сути своей являющегося разновидностью авторегрессионого фильтра, множители в векторах которого и задают полином L. Декодер, построенный по такому алгоритму, требует не более 3t операций умножения в каждой из итерации, количество которых не превышает 2t. Таким образом, решение поставленной задачи укладывается всего в 6t2 операций умножения. Фактически поиск локатора сводится к решению системы из 2t уравнений – по одному уравнению на каждый символ синдрома – c t неизвестными. Неизвестные члены и есть позиции искаженных символов в кодовом слове v. Легко видеть, если количество ошибок превышает t, система уравнений становится неразрешима и восстановить разрушенную информацию в этом случае не представляется возможным. Блок-схема алгоритма Берлекэмпа-Месси приведена на рис. 5, а его законченная программа реализация содержится в листинге 2. Рисунок 5. Структурная схема алгоритма Берлекэмпа-Месси Корни полинома Коль скоро полином локатора ошибки нам известен, его корни определяют местоположение искаженных символов в принятом кодовом слове. Остается эти корни найти. Чаще всего для этого используется процедура Ченя (Chien search), аналогичная по своей природе обратному преобразованию Фурье и фактически сводящаяся к тупому перебору (brute force, exhaustive search) всех возможных вариантов. Все 2m возможных символов один за другим подставляются в полином локатора в порядке социалистической очереди и затем выполняется расчет полинома. Если результат обращается в ноль – считается, что искомые корни найдены. Восстановление данных Итак, мы знаем, какие символы кодового слова искажены, но пока еще не готовы ответить на вопрос: как именно они искажены. Используя полином синдрома и корни полинома локатора, мы можем определить характер разрушений каждого из искаженных символов. Обычно для этой цели используется алгоритм Форни (Forney), состоящий из двух стадий: сначала путем свертки полинома синдрома полиномом локатора L мы получаем некоторый промежуточный полином, условно обозначаемый греческой буквой W. Затем на основе W-полинома вычисляется нулевая позиция ошибки (zero error location), которая в свою очередь делится на производную от L-полинома. В результате получается битовая маска, каждый из установленных битов которой соответствует искаженному биту и для восстановления кодового слова в исходный вид все искаженные биты должны быть инвертированы, что осуществляется посредством логической операции XOR. На этом процедура декодирования принятого кодового слова считается законченной. Остается отсечь n – k символов четности, и полученное информационное слово готово к употреблению. Исходный текст декодера Ниже приводится исходный текст полноценного декодера Рида-Соломона, снабженный минимально разумным количеством комментариев. К сожалению, в рамках журнальной статьи подробное комментирование кода декодера невозможно, поскольку потребовало бы очень много места. При возникновении трудностей в анализе этого листинга обращайтесь к блок-схемам, приведенным на рис. 3, 4 и 5 – они помогут. Листинг 2. Исходный текст простейшего декодера Рида-Соломона /*----------------------------------------------------------------------------------------------------- * * декодер Рида-Соломона * ===================== * * Процедура декодирования кодов Рида-Соломона состоит из нескольких шагов: сначала мы вычисляем * 2t-символьный синдром путем постановки alpha**i в recd(x), где recd – полученное кодовое слово, * предварительно переведенное в индексную форму. По факту вычисления recd(x) мы записываем * очередной символ синдрома в s[i], где i принимает значение от 1 до 2t, оставляя s[0] равным нулю. * Затем, используя итеративный алгоритм Берлекэмпа, мы находим полином локатора ошибки – elp[i]. * Если степень elp превышает собой величину t, мы бессильны скорректировать все ошибки и ограничиваемся * выводом сообщения о неустранимой ошибке, после чего совершаем аварийный выход из декодера. * Если же степень elp не превышает t, мы подставляем alpha**i, где i = 1..n в elp для вычисления * корней полинома. Обращение найденных корней дает нам позиции искаженных символов. Если количество * определенных позиций искаженных символов меньше степени elp, искажению подверглось более чем t * символов и мы не можем восстановить их. Во всех остальных случаях восстановление оригинального * содержимого искаженных символов вполне возможно. В случае, когда количество ошибок заведомо велико, * для их исправления декодируемые символы проходят сквозь декодер без каких-либо изменений. * * на основе исходных текстов Simon Rockliff, от 26.06.1991, распространяемых по лицензии GNU –––––––––––––––––––––––––––––––––––––––––––––––––––––––––--------------------------------------------*/ decode_rs() { int i, j, u, q; int s[n-k+1]; // полином синдрома ошибки int elp[n – k + 2][n - k]; // полином локатора ошибки лямбда int d[n-k+2]; int l[n-k+2]; int u_lu[n-k+2], int count=0, syn_error=0, root[t], loc[t], z[t+1], err[n], reg[t+1]; // переводим полученное кодовое слово в индексную форму для упрощения вычислений for (i = 0; i < n; i++) recd[i] = index_of[recd[i]]; // вычисляем синдром //------------------------------------------------------------------------------------------------- for (i = 1; i <= n - k; i++) { s[i] = 0; // инициализация s-регистра (на его вход по умолчанию поступает ноль) // выполняем s[i] += recd[j]*ij т.е. берем очередной символ декодируемых данных, умножаем его // на порядковый номер данного символа, умноженный на номер очередного оборота и складываем // полученный результат с содержимым s-регистра по факту исчерпания всех декодируемых символов, // мы повторяем весь цикл вычислений опять – по одному разу для каждого символа четности for (j=0; j<n; j++) if (recd[j]!=-1) s[i]^= alpha_to[(recd[j]+i*j)%n]; if (s[i]!=0) syn_error=1; // если синдром не равен нулю, взводим флаг ошибки // преобразуем синдром из полиномиальной формы в индексную s[i] = index_of[s[i]]; } // коррекция ошибок //------------------------------------------------------------------------------------------------- if (syn_error) // если есть ошибки, пытаемся их скорректировать { // вычисление полинома локатора лямбда //----------------------------------------------------------------------------------------------- // вычисляем полином локатора ошибки через итеративный алгоритм Берлекэмпа. Следуя терминологии // Lin and Costello (см. "Error Control Coding: Fundamentals and Applications" Prentice Hall 1983 // ISBN 013283796) d[u] представляет собой m («мю»), выражающую расхождение (discrepancy), // где u = m + 1 и m есть номер шага из диапазона от –1 до 2t. У Блейхута та же самая величина // обозначается D(x) («дельта») и называется невязкой. l[u] представляет собой степень elp // для данного шага итерации, u_l[u] представляет собой разницу между номером шага и степенью elp, // инициализируем элементы таблицы d[0] = 0; // индексная форма d[1] = s[1]; // индексная форма elp[0][0] = 0; // индексная форма elp[1][0] = 1; // полиномиальная форма for (i = 1; i < n - k; i++) { elp[0][i] = -1; // индексная форма elp[1][i] = 0; // полиномиальная форма } l[0] = 0; l[1] = 0; u_lu[0] = -1; u_lu[1] = 0; u = 0; do { u++; if (d[u] == -1) { l[u + 1] = l[u]; for (i = 0; i <= l[u]; i++) { elp[u+1][i] = elp[u][i]; elp[u][i] = index_of [elp[u][i]]; } } else { // поиск слов с наибольшим u_lu[q], таких что d[q]!=0 q = u - 1; while ((d[q] == -1) && (q>0)) q--;
// найден первый ненулевой d[q] if (q > 0) { j=q ; do { j-- ; if ((d[j]!=-1) && (u_lu[q]<u_lu[j])) q = j ; } while (j>0); }; // как только мы найдем q, такой что d[u]!=0 и u_lu[q] есть максимум // запишем степень нового elp полинома if (l[u] > l[q]+u-q) l[u+1] = l[u]; else l[u+1] = l[q]+u-q; // формируем новый elp(x) for (i = 0; i < n - k; i++) elp[u+1][i] = 0; for (i = 0; i <= l[q]; i++) if (elp[q][i]!=-1) elp[u+1][i+u-q]=alpha_to [(d[u]+n-d[q]+elp[q][i])%n]; for (i=0; i<=l[u]; i++) { elp[u+1][i] ^= elp[u][i]; // преобразуем старый elp в индексную форму elp[u][i] = index_of[elp[u][i]]; } } u_lu[u+1] = u-l[u+1]; // формируем (u + 1) невязку //------------------------------------------------------------------------------------------------ if (u < n-k) // на последней итерации расхождение не было обнаружено { if (s[u + 1]!=-1) d[u+1] = alpha_to[s[u+1]]; else d[u + 1] = 0; for (i = 1; i <= l[u + 1]; i++) if ((s[u + 1 - i] != -1) && (elp[u + 1][i]!=0)) d[u+1] ^= alpha_to[(s[u+1-i]+index_of[elp[u+1][i]])%n]; // переводим d[u+1] в индексную форму d[u+1] = index_of[d[u+1]]; } } while ((u < n-k) && (l[u+1]<=t)); // расчет локатора завершен //----------------------------------------------------- u++ ; if (l[u] <= t) { // коррекция ошибок возможна
// переводим elp в индексную форму for (i = 0; i <= l[u]; i++) elp[u][i] = index_of[elp[u][i]]; // нахождение корней полинома локатора ошибки //---------------------------------------------- for (i = 1; i <= l[u]; i++) reg[i] = elp[u][i]; count = 0; for (i = 1; i <= n; i++) { q = 1 ; for (j = 1; j <= l[u]; j++) if (reg[j] != -1) { reg[j] = (reg[j]+j)%n; q ^= alpha_to[reg[j]]; } if (!q) { // записываем корень и индекс позиции ошибки root[count] = i; loc[count] = n-i; count++; } } if (count == l[u]) { // нет корней – степень elp < t ошибок // формируем полином z(x) for (i = 1; i <= l[u]; i++) // Z[0] всегда равно 1 { if ((s[i]!=-1) && (elp[u][i]!=-1)) z[i] = alpha_to[s[i]] ^ alpha_to[elp[u][i]]; else if ((s[i]!=-1) && (elp[u][i]==-1)) z[i] = alpha_to[s[i]]; else if ((s[i]==-1) && (elp[u][i]!=-1)) z[i] = alpha_to[elp[u][i]]; else z[i] = 0 ; for (j=1; j<i; j++) if ((s[j]!=-1) && (elp[u][i-j]!=-1)) z[i] ^= alpha_to[(elp[u][i-j] + s[j])%n]; // переводим z[i] в индексную форму z[i] = index_of[z[i]]; } // вычисление значения ошибок в позициях loc[i] //---------------------------------------------------------------------------------------------- for (i = 0; i<n; i++) { err[i] = 0; // переводим recd[] в полиномиальную форму if (recd[i]!=-1) recd[i] = alpha_to[recd[i]]; else recd[i] = 0; } // сначала вычисляем числитель ошибки for (i = 0; i < l[u]; i++) { err[loc[i]] = 1; for (j=1; j<=l[u]; j++) if (z[j]!=-1) err[loc[i]] ^= alpha_to [(z[j]+j*root[i])%n]; if (err[loc[i]]!=0) { err[loc[i]] = index_of[err[loc[i]]]; q = 0 ; // формируем знаменателькоэффициента ошибки for (j=0; j<l[u]; j++) if (j!=i) q+=index_of[1^alpha_to[(loc[j]+root[i])%n]]; q = q % n; err[loc[i]] = alpha_to [(err[loc[i]]-q+n)%n]; // recd[i] должен быть в полиномиальной форме recd[loc[i]] ^= err[loc[i]]; } } } else // нет корней, решение системы уравнений невозможно, т.к. степень elp >= t { // переводим recd[] в полиномиальную форму for (i=0; i<n; i++) if (recd[i]!=-1) recd[i] = alpha_to[recd[i]]; else recd[i] = 0; // выводим информационное слово как есть } else // степень elp > t, решение невозможно { // переводим recd[] в полиномиальную форму for (i=0; i<n; i++) if (recd[i]!=-1) recd[i] = alpha_to[recd[i]] ; else recd[i] = 0 ; // выводим информационное слово как есть } else // ошибок не обнаружено for (i=0;i<n;i++) if(recd[i]!=-1)recd[i]=alpha_to[recd[i]]; else recd[i]=0; } Интерфейс с библиотекой ElByECC.DLL Программная реализация кодера/декодера Рида-Соломона, приведенная в листингах 1, 2, достаточно наглядна, но крайне непроизводительна и нуждается в оптимизации. Как альтернативный вариант можно использовать готовые библиотеки от сторонних разработчиков, входящие в состав программных комплексов, так или иначе связанных с обработкой корректирующих кодов Рида-Соломона. Это и утилиты прожига/копирования/восстановления лазерных дисков, и драйвера ленточных накопителей (от стримера до Арвида), и различные телекоммуникационные комплексы и т. д. Как правило, все эти библиотеки являются неотъемлемой частью самого программного комплекса и потому никак не документируется. Причем восстановление прототипов интерфейсных функций представляет весьма нетривиальную задачу, требующую от исследователя не только навыков дизассемблирования, но и знаний высшей математики, иначе смысл всех битовых манипуляций останется совершенно непонятным. Насколько законно подобное дизассемблирование? Да, дизассемблирование сторонних программных продуктов действительно запрещено, но тем не менее оно законно. Здесь уместно провести аналогию со вскрытием пломб вашего телевизора, влекущее потерю гарантии, но отнюдь не приводящее к уголовному преследованию. Также никто не запрещает вызывать функции чужой библиотеки из своей программы. Нелегально распространять эту библиотеку в составе вашего программного обеспечения действительно нельзя, но что мешает вам попросить пользователя установить данную библиотеку самостоятельно? Ниже приводится описание важнейших функций библиотеки ElByECC.DLL, входящей в состав известного копировщика защищенных лазерных дисков Clone CD, условно-бесплатную копию которого можно скачать c cайта: http://www.elby.ch/. Сам Clone CD проработает всего лишь 21 день, а затем потребует регистрации, однако на продолжительность использования библиотеки ElByECC.DLL не наложено никаких ограничений. Моими усилиями был создан h-файл, содержащий прототипы основных функций библиотеки ElByECC.DLL, специальная редакция которого была любезно предоставлена для журнала «Системный администратор». Несмотря на то, что библиотека ElByECC.DLL ориентирована на работу с секторами лазерных дисков, она может быть приспособлена и для других целей, например, построения отказоустойчивых дисковых массивов, о которых говорилось в предыдущей статье. Краткое описание основных функций библиотеки приводится ниже. Подключение библиотеки ElByECC.DLL к своей программе Существуют по меньшей мере два способа подключения динамических библиотек к вашим программам. При динамической компоновке адреса требуемых функций определяются посредством вызова GetProcAddress, причем сама библиотека ElByECC.DLL должна быть предварительно загружена через LoadLibrary. Это может выглядеть, например, так (обработка ошибок для простоты опущена): Листинг 3. Динамическая загрузка библиотеки ElByECC.DLL HANDLE h; int (__cdecl *CheckECCAndEDC_Mode1) (char *userdata, char *header, char *sector); h=LoadLibrary("ElbyECC.dll"); CheckECCAndEDC_Mode1 = GetProcAddress(h, "CheckECCAndEDC_Mode1"); Статическая компоновка предполагает наличие специального lib-файла, который может быть автоматически сгенерирован утилитой implib из пакета Borland C++ любой подходящей версии, представляющую собой утилиту командной строки, вызываемую так: implib.exe -a ElByECC.lib ElByECC.lib GenECCAndEDC_Mode1 Функция GenECCAndEDC_Mode1 осуществляет генерацию корректирующих кодов на основе 2048-байтового блока пользовательских данных и имеет следующий прототип: Листинг 4. Прототип функции GenECCAndEDC_Mode1 // указатель на массив из 2048 байт GenECCAndEDC_Mode1(char *userdata_src, // указатель на заголовок char *header_src, struct RAW_SECTOR_MODE1 *raw_sector_mode1_dst)
Листинг 5. Структура сырого сектора struct RAW_SECTOR_MODE1 { BYTE SYNC[12]; // синхрогруппа BYTE ADDR[3]; // абсолютный адрес сектора BYTE MODE; // тип сектора BYTE USER_DATA[2048]; // пользовательские данные BYTE EDC[4]; // контрольная сумма BYTE ZERO[8]; // нули (не используется) BYTE P[172]; // P-байты четности BYTE Q[104]; // Q-байты четности }; При успешном завершении функция возвращает ненулевое значение и ноль в противном случае. CheckSector Функция CheckSector осуществляет проверку целостности сектора по контрольной сумме и при необходимости выполняет его восстановление по избыточным кодам Рида-Соломона. Листинг 6. Прототип функции CheckSector // указатель на секторный буфер CheckSector(struct RAW_SECTOR *sector, int DO); // только проверка/лечение
При успешном завершении функция возвращает ненулевое значение и ноль, если сектор содержит ошибку (в режиме TEST ONLY) или если данные восстановить не удалось (при вызове функции в режиме лечения). Для предотвращения возможной неоднозначности рекомендуется вызывать данную функцию в два приема. Первый раз – в режиме тестирования для проверки целостности данных, и второй раз – в режиме лечения (если это необходимо). Финал Ниже приведен законченный примем использования корректирующих кодов на практике, пригодный для решения реальных практических задач. Листинг 7. Пример вызова функций ElByECC.DLL из своей программы /*---------------------------------------------------------------------------------------------------- * * демонстрация ElByECC.DLL * ======================== * * Данная программа демонстрирует работу с библиотекой ElByECC.DLL, генерируя избыточные коды * Рида-Соломона на основе пользовательских данных, затем умышленно искажает их и вновь восстанавливает. * Количество разрушаемых байт передается в первом параметре командной строки (по умолчанию – 6) -----------------------------------------------------------------------------------------------------*/ #include <stdio.h> #include "ElByECC.h" // декомпилировано автором // рушить по умолчанию #define _DEF_DMG 6 // сколько байт рушить? #define N_BYTES_DAMAGE ((argc>1)?atol(argv[1]):_DEF_DMG) main(int argc, char **argv) { int a; // заголовок сектора char stub_head[HEADER_SIZE]; // область пользовательских данных char user_data[USER_DATA_SIZE]; // сектор для искажений struct RAW_SECTOR_MODE1 raw_sector_for_damage; // контрольная копия сектора struct RAW_SECTOR_MODE1 raw_sector_for_compre; // TITLE //--------------------------------------------------------------------------------------------------- printf("= ElByECC.DLL usage demo example by KK\n"); // инициализация пользовательских данных //--------------------------------------------------------------------------------------------------- printf("user data initialize..............."); // user_data init for (a = 0; a < USER_DATA_SIZE; a++) user_data[a] = a; // src header init memset(stub_head, 0, HEADER_SIZE); stub_head[3] = 1; printf("+OK\n"); // генерация кодов Рида-Соломона на основе // пользовательских данных //--------------------------------------------------------------------------------------------------- printf("RS-code generate..................."); a = GenECCAndEDC_Mode1(user_data, stub_head, &raw_sector_for_damage); if (a == ElBy_SECTOR_ERROR) { printf("-ERROR!\x7\n"); return -1;} memcpy(&raw_sector_for_compre, &raw_sector_for_damage, RAW_SECTOR_SIZE); printf("+OK\n"); // умышленное искажение пользовательских данных //--------------------------------------------------------------------------------------------------- printf("user-data %04d bytes damage........", N_BYTES_DAMAGE); for (a=0;a<N_BYTES_DAMAGE;a++) raw_sector_for_damage.USER_DATA[a]^=0xFF; if(!memcmp(&raw_sector_for_damage, &raw_sector_for_compre,RAW_SECTOR_SIZE)) printf("-ERR: NOT DAMAGE YET\n"); else printf("+OK\n"); // проверка целостности пользовательских данных //--------------------------------------------------------------------------------------------------- printf("user-data check...................."); a = CheckSector((struct RAW_SECTOR*) &raw_sector_for_damage, ElBy_TEST_ONLY); if (a==ElBy_SECTOR_OK){ printf("-ERR:data not damage\x7\n");return -1;}printf(".data damge\n"); // восстановление пользовательских данных //--------------------------------------------------------------------------------------------------- printf("user-data recorver................."); a = CheckSector((struct RAW_SECTOR*) &raw_sector_for_damage, ElBy_REPAIR); if (a == ElBy_SECTOR_ERROR) { printf("-ERR: NOT RECORVER YET\x7\n"); return -1; } printf("+OK\n"); // проверка успешности восстановления //--------------------------------------------------------------------------------------------------- printf("user-data recorver check..........."); if(memcmp(&raw_sector_for_damage, &raw_sector_for_compre,RAW_SECTOR_SIZE)) printf("-ERR: NOT RECORVER YET\x7\n"); else printf("+OK\n"); printf("+OK\n"); return 1; } |
| Комментарии |
| Добавить комментарий |
|
Комментарии могут оставлять только зарегистрированные пользователи |
|










 КРИС КАСПЕРСКИ
КРИС КАСПЕРСКИ